統計のコツのこつ(15)

このブログは「すぐに役立つ統計のコツ」(オーム社)をもとに、チョット付け加えておきたい事を書いています。
重複するかも知れませんが、ご参考になればと思っています。

 

それでは、「すぐに役立つ統計のコツ」第７章(94ページ)を開いて下さい。

 

本書の例題(データ)は下記の情報統計研究所(HP)からダウンロード出来ますのでご利用下さい。

 

本書の第７章は、主な「多変量解析」をご紹介しています。

 

● 重回帰分析(本書94ページ)について
統計のコツのこつ(12)では、直線回帰と曲線回帰での回帰モデル(回帰式)についてご紹介しました。
すなわち、目的変数を１つの説明変数で示す回帰モデルでした。
重回帰分析は、２つ以上の説明変数で目的変数を説明するための最適な回帰モデルを導くことです。
よって、
そのモデル式は、
　Ｙ＝a1・X1＋a2・X2＋・・・＋ai・Xi

 

となり、
目的変数(Y)は複数の説明変数(X)と係数(a)によって、どの程度正確に予測できるかで回帰モデルの良し悪しが決まります。

 

「すぐに役立つ統計のコツ」第７章(95ページ)の「例題 15」では、スギ花粉飛散数を天候(気温、湿度、天気)で予測する回帰モデルについて、その分析方法を述べています。

 

ここでは、
もっと分かりやすい仮想例題で、単純な重回帰分析やってみましょう。

 

 

Excelによる重回帰分析の方法は、本書をみて下さい。

Excelの出力結果(回帰モデル式)は次の通りです。

 

Ｙ＝91.168＋2.083・Ｘ1＋0.5194・Ｘ２

 

重決定 R2＝0.968

 

Ｘ１の有意性：ｔ＝4.914（ｐ＝0.0079）
Ｘ２の有意性：ｔ＝4.155（ｐ＝0.0142）

 

Ｘ１とＸ２の説明変数は共に有意であり、目的変数に有用な変数と言えます。

 

医学や看護の研究では、回帰モデルよりも目的変数に最も影響する説明変数は何かを問う場合が多いと思います。
その場合でも、
回帰モデルが有用であるかどうか(モデルの有意性)を判断しなければなりません。
もし、有用でないなら他の方法を考える必要があります。

 

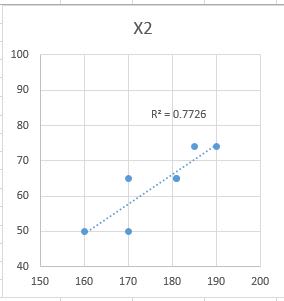
下図は、「ＹとＸ１」、「ＹとＸ２」、そして「Ｙと予測値Ｙ'」の散布図と決定係数Ｒ^2です。

 

 

 

 

 

 

 

 次回は、ロジスティック回帰分析です。

 

情報統計研究はここから