このブログは「すぐに役立つ統計のコツ」(オーム社)でご紹介できなかった統計に関する色々な事を書いています。
今回は、「相関と回帰」に関するチョットしたコツをご紹介しましょう。
今回は、「相関と回帰」に関するチョットしたコツをご紹介しましょう。
それでは、「すぐに役立つ統計のコツ」第6章(66ページ)を開いて下さい。
本書の例題(データ)は下記の情報統計研究所(HP)からダウンロード出来ますのでご利用下さい。

相関係数は、2つの標本間の直線関係が強いか弱いかであり、
相関回帰は、2つの標本の関係を直線又は曲線の回帰式で表したものです。
相関回帰は、2つの標本の関係を直線又は曲線の回帰式で表したものです。
相関関係は、
数学のY=aX+bに良くフイットする関係(Xを知ってYを予測する)を Linear Fit(線形回帰又は単回帰)と言います。
一方、
Polynomial Fit, Quadratic(2次多項式)、Cubic(3次多項式)、Quartic(4次多項式)などを多項式回帰と言います。
その他にも、
Expoential Fit(指数関数のあてはめ)など非線形回帰(直線回帰以外を言う)などがあります。
数学のY=aX+bに良くフイットする関係(Xを知ってYを予測する)を Linear Fit(線形回帰又は単回帰)と言います。
一方、
Polynomial Fit, Quadratic(2次多項式)、Cubic(3次多項式)、Quartic(4次多項式)などを多項式回帰と言います。
その他にも、
Expoential Fit(指数関数のあてはめ)など非線形回帰(直線回帰以外を言う)などがあります。
「すぐに役立つ統計のコツ」では、非線形のデータを対数変換で線形関係にする方法を紹介しています。
ここでは、
対数変換をしなかった場合の多項式による当てはめをやってみましょう。
例題は本書の表3.2(11ページ)のGOTとGPTです
ここでは、
対数変換をしなかった場合の多項式による当てはめをやってみましょう。
例題は本書の表3.2(11ページ)のGOTとGPTです
本書のExcelの方法と同じやり方で「散布図」→「近似曲線の追加」で1次~3次多項式にフイットさせると、
下図の非線形関係を知ることが出来ます。
下図の非線形関係を知ることが出来ます。
決定係数 R^2 は次の様になります。
・1次式: R^2=0.7077
・2次式: R^2=0.7237
・3次式: R^2=0.7436
・2次式: R^2=0.7237
・3次式: R^2=0.7436
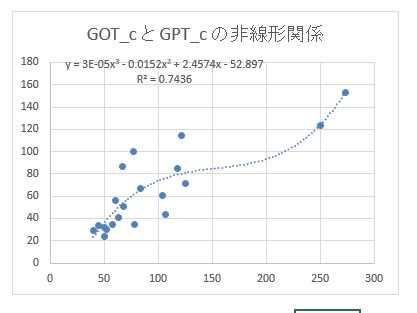
これを、
自然対数変換すれば単純な1次式(Y=aX+b)で表すことが出来ます(本書70ページ、図6.1)。
しかし、GOTとGPTの関係は対数変換値となり、実数値を1次式に当てはめることは出来ません。
自然対数変換すれば単純な1次式(Y=aX+b)で表すことが出来ます(本書70ページ、図6.1)。
しかし、GOTとGPTの関係は対数変換値となり、実数値を1次式に当てはめることは出来ません。
***
重回帰モデルは、説明変数は2ツ以上あるものです。
***
重回帰モデルは、説明変数は2ツ以上あるものです。
***
次回は、
引き続き「すぐに役立つ統計のコツ」の第6章から、分割表形式の相関をご紹介します。
引き続き「すぐに役立つ統計のコツ」の第6章から、分割表形式の相関をご紹介します。

情報統計研究はここから









