情報統計研究所(統計分析のご相談ご依頼)のアクセスはここから。
前回の末梢血中好塩基球数( Ba ) と血清IgE値( IgE ) の実測データを用いて、実際に、時差相関係数を求めてみましょう。
Ba と IgE の測定単位が違いますので、次により、標準化(正規化変換)を行います。すなわち、
Ba ( Xi ) の mean±SD=125.35±32.62、
IgE ( Yi ) の mean±SD=583.48±183.42、
から、
( Xi-125.35 ) / 32.62 、( Yi-583.48 ) / 183.42
により標準化(正規化変換)したデータを図1に示します。
図1 標準化した時系列データ
図1のデータについて、図2のようにデータを一つずつずらせて
r[k]=Sxy[k]/SQRT( Sxx[0] ・Syy[0] )
を計算しますと、時差[k](k=Lag Time)の相関係数が求まります。。
図2 時差相関係数の求め方
BaとIgEの時差相関係数は次の通りです。
r[0]=0.537、r[1]=0.549、r[2]=0.552、・・・、r[10]=-0.149
Ba とI gE の時差はLag=2 で最大であり、Ba の増加と IgE の上昇には2日の時差があるようです。
さて、MSエクセルの関数を使っての計算が面倒なら・・・、「R」を使用すれば簡単に求める事が出来ます。
「R」では ccf() が用意されており、
ccf ( X , Y )
で図3 の出力結果が得られます。
図3 「R」による時差相関プロット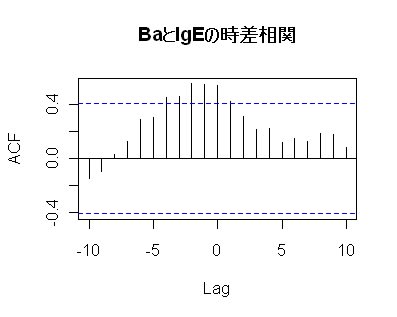
時系列データでは、単相関で相関が見られなくても、時差を与える事で相関関係や循環性などの情報が得られる事もあります。
次回は自己相関について、心拍(R-R間隔)を取り上げたいと思います。









