命題
x,y の多項式 f(x,y)が f(x,y)=f(y,x) を満たし、
s=x+y , t=xy , u=x-y , v=x²
としたとき、fは s, tの関数として表される。
証明
下記は簡単に計算される。
x=(s+u)/2 , y=(s-u)/2 , s2-u2=4xy=4t ・・・・・・・①
条件から
f(x,y)=( f(x,y)+f(y,x) )/2
である。また、x,yの多項式は一般に f=Σ Amn xm yn と表されるから
f(x,y)=Σ (Amn /2)(xm yn +ym xn ) ・・・・②
となる。ここで、対称なので m≧n としても一般性は失わない。
xm yn +ym xn =(xy)n (xm-n +ym-n )=(tn/2m-n) { (s+u)m-n +(s-u)m-n }
となる。これは s,u の多項式であるが、この値は u → ±uとしても変わらないから
(s+u)m-n +(s-u)m-n =Σ Bpq spu2q =Σ Bpq sp (s2-4t)q
と表される。ここで、①を使った。
②に戻すと、fは s,t の関数とわかる。
以上
最新の画像[もっと見る]
-
 電源や抵抗の電力が 電圧と電流の積 VIとなる理由
2年前
電源や抵抗の電力が 電圧と電流の積 VIとなる理由
2年前
-
 関数 f(x)=x²-2ax+a+2 とx軸の交点が 1<x<3 の区間に1つだけあるときの aの条件
3年前
関数 f(x)=x²-2ax+a+2 とx軸の交点が 1<x<3 の区間に1つだけあるときの aの条件
3年前
-
 x² 上の任意の2つの点の法線の交点の作る集合
3年前
x² 上の任意の2つの点の法線の交点の作る集合
3年前
-
 e^x上の任意の2つの点の法線の交点の作る集合
3年前
e^x上の任意の2つの点の法線の交点の作る集合
3年前
-
 e^x上の任意の2つの点の法線の交点の作る集合
3年前
e^x上の任意の2つの点の法線の交点の作る集合
3年前
-
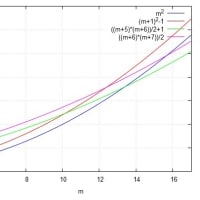 とある2つの数列 An, Bnの差が指定されたとき、最小の nを求める
4年前
とある2つの数列 An, Bnの差が指定されたとき、最小の nを求める
4年前
-
 点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
-
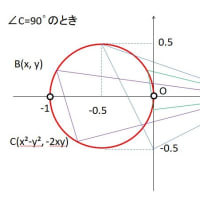 点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
-
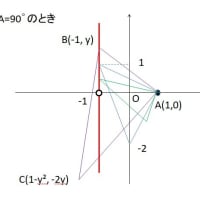 点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
-
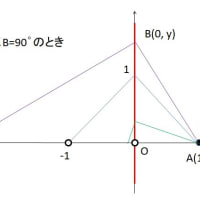 点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
「算数」カテゴリの最新記事
 長方形の中心を通り、直交する2直線によって、等分割する問題
長方形の中心を通り、直交する2直線によって、等分割する問題 sin/cosを含む連立方程式の解法
sin/cosを含む連立方程式の解法 関数 f(x)=x²-2ax+a+2 とx軸の交点が 1<x<3 の区間に1つだけあるときの aの条件
関数 f(x)=x²-2ax+a+2 とx軸の交点が 1<x<3 の区間に1つだけあるときの aの条件 ある線分とパラメータa,bで表される円があるとき、円が線分を含まないa,bの範囲
ある線分とパラメータa,bで表される円があるとき、円が線分を含まないa,bの範囲 円の外部にある点Pから、その円への接線との交点の中点をQとする。Pが移動するとき...
円の外部にある点Pから、その円への接線との交点の中点をQとする。Pが移動するとき... 点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡...
点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡... 2つの曲線 y=x² と y=(x-a)²/4 (a>0)で囲まれた領域で x+2y の最大最小値
2つの曲線 y=x² と y=(x-a)²/4 (a>0)で囲まれた領域で x+2y の最大最小値 放物線が放物線上を転がるときの軌跡
放物線が放物線上を転がるときの軌跡 ある変数変換に対する領域の形状変化
ある変数変換に対する領域の形状変化 x,yの多項式 f(x,y)が f(x,y)=f(y,x) を満たすときの形式
x,yの多項式 f(x,y)が f(x,y)=f(y,x) を満たすときの形式














