1. まえがき
円 x²+y²=1 の外部にある点 P(a,b) から、その円への接線との交点の中点をQとする。Pが
y=-x+1
または
(x+1)²+(y+1)²=2
を移動するとき、Qの軌跡を求めよという問題があった。
2. 中点Qの座標の計算
指定の円上の点(x',y')を通る接線は
x'x+y' y=1
これが、P(a,b)を通るから
ax'+by'=1・・・・・①
また y'=±√(1-x'²) だから
ax'±b√(1-x'²)=1 → (ax'-1)²=b²(1-x'²) → (a²+b²)x'²-2ax'+(1-b²)=0 → x'={a±√(a²+b²-1)}/(a²+b²)
ここで、x'の点は2つあるとき、その中点を (u,v) とすると
u=(x'₁+x'₂)/2=a/(a²+b²)・・・・②
となる。
①において、ax',by'は対称だから、中点 vは②において、a → b としたものになるから
v=b/(a²+b²)・・・・③
となる。
②③から
v/u=b/a , au+bv=1・・・・④
をえる。
3. 点Pの軌跡が y=-x+1のとき
点Pは (a,b)=(x,1-x) だから、④で、a,bを消して
v/u=(1-x)/x=(1/x)-1 → x=1/((v/u)+1)=u/(u+v)
xu+(1-x)v=1
となる。これらから、xを消すと
{u/(u+v)}u+{1-u/(u+v)}v=1 → u²+(u+v)v-uv=u+v → u²+v²-u-v=0
→ (u-1/2)²+(v-1/2)²=1/2
という円(の一部、元の円の内部のときは無い)になる。
4. 点Pの軌跡が (x+1)²+(y+1)²=2 のとき
点Pは (a,b)=(x, -1±√{2-(x+1)²}) だから、同様に④から
v/u=b/a=[-1±√{2-(x+1)²}]/x・・・・・⑤
xu+{-1±√{2-(x+1)²}v=1
これらから {-1±√{2-(x+1)²} を消すと
xu+xv²/u=1 → x=u/(u²+v²)・・・・・⑥
また、⑤で±√ で整理して、2乗を取ると
(xv/u+1)²=2-(x+1)² → (v²/u²+1)x²+2(v/u+1)x=0
→ x=0 or x=-2(v/u+1)/(v²/u²+1)=-2u(v+u)/(v²+u²)
⑥と合わせると
u=0
または u≠0 とすると
u/(u²+v²)=-2u(v+u)/(v²+u²) → v+u=0・・・・⑦
ここで、②から、u=0 → 常に a=0 となるが、aは円の軌跡なので、aは常に0ではなく、
u=0 は無い。したがって、解は⑦の直線(の一部)のみとなる。
以上
最新の画像[もっと見る]
-
 電源や抵抗の電力が 電圧と電流の積 VIとなる理由
2年前
電源や抵抗の電力が 電圧と電流の積 VIとなる理由
2年前
-
 関数 f(x)=x²-2ax+a+2 とx軸の交点が 1<x<3 の区間に1つだけあるときの aの条件
3年前
関数 f(x)=x²-2ax+a+2 とx軸の交点が 1<x<3 の区間に1つだけあるときの aの条件
3年前
-
 x² 上の任意の2つの点の法線の交点の作る集合
3年前
x² 上の任意の2つの点の法線の交点の作る集合
3年前
-
 e^x上の任意の2つの点の法線の交点の作る集合
3年前
e^x上の任意の2つの点の法線の交点の作る集合
3年前
-
 e^x上の任意の2つの点の法線の交点の作る集合
3年前
e^x上の任意の2つの点の法線の交点の作る集合
3年前
-
 とある2つの数列 An, Bnの差が指定されたとき、最小の nを求める
4年前
とある2つの数列 An, Bnの差が指定されたとき、最小の nを求める
4年前
-
 点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
-
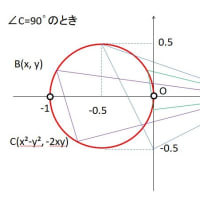 点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
-
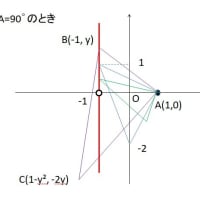 点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
-
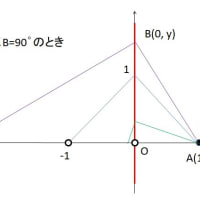 点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
「算数」カテゴリの最新記事
 長方形の中心を通り、直交する2直線によって、等分割する問題
長方形の中心を通り、直交する2直線によって、等分割する問題 sin/cosを含む連立方程式の解法
sin/cosを含む連立方程式の解法 関数 f(x)=x²-2ax+a+2 とx軸の交点が 1<x<3 の区間に1つだけあるときの aの条件
関数 f(x)=x²-2ax+a+2 とx軸の交点が 1<x<3 の区間に1つだけあるときの aの条件 ある線分とパラメータa,bで表される円があるとき、円が線分を含まないa,bの範囲
ある線分とパラメータa,bで表される円があるとき、円が線分を含まないa,bの範囲 円の外部にある点Pから、その円への接線との交点の中点をQとする。Pが移動するとき...
円の外部にある点Pから、その円への接線との交点の中点をQとする。Pが移動するとき... 点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡...
点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡... 2つの曲線 y=x² と y=(x-a)²/4 (a>0)で囲まれた領域で x+2y の最大最小値
2つの曲線 y=x² と y=(x-a)²/4 (a>0)で囲まれた領域で x+2y の最大最小値 放物線が放物線上を転がるときの軌跡
放物線が放物線上を転がるときの軌跡 ある変数変換に対する領域の形状変化
ある変数変換に対する領域の形状変化 x,yの多項式 f(x,y)が f(x,y)=f(y,x) を満たすときの形式
x,yの多項式 f(x,y)が f(x,y)=f(y,x) を満たすときの形式














