級数 Σ(log(n))³/n^a (a>1) の収束の判定方法
1.
f(x)=(log(x))³/x^a (a>1)
とする。
f'(x)=3(log x)²(1/x)/x^a+(log x)³(-ax^(-a-1))
={(log x)²/x^(-a-1)}(3-alog x)
したがって、x>exp(3/a) ならば、f'(x)<0 となって、f(x)は単調減少とわかる。すると、
f(x)が単調減少の時、よく知られているように
Σ[n=k,∞] f(n)<∫[k-1,∞]f(x)dx
なお、級数の収束性は始めの有限個数を取り除いても変わらない。
2.
以上のことから、k=[exp(3/a)]+1 とすると
Σ[n=k+1,∞](log(n))³/n^a<∫[k,∞]{(log(x))³/x^a}dx
となり、右辺が有限であれば級数は収束する。
y=log x と変数変換して、dy=dx/x, x^a=e^(ay) だから
A=∫[k,∞]{(log(x))³/x^a}dx=∫[log k,∞]{y³x^(-a+1)}dy
=∫[log k,∞]{y³e^((-a+1)y)}dy
z=(a-1)y と変換して
A=(a-1)⁻⁴∫[(log k)/(a-1),∞]{z³e^(-z)}dz
最後の積分は部分積分してz³の次数を下げれば、有限となることはすぐわかる。ゆえに、
求める級数は収束する。
3.
なお、(log(n))^m (m≧0) のときも、同じ論理で、級数
Σ {(log(n))^m}/n^a (a>1) は収束する。
以上
最新の画像[もっと見る]
-
 電源や抵抗の電力が 電圧と電流の積 VIとなる理由
2年前
電源や抵抗の電力が 電圧と電流の積 VIとなる理由
2年前
-
 関数 f(x)=x²-2ax+a+2 とx軸の交点が 1<x<3 の区間に1つだけあるときの aの条件
3年前
関数 f(x)=x²-2ax+a+2 とx軸の交点が 1<x<3 の区間に1つだけあるときの aの条件
3年前
-
 x² 上の任意の2つの点の法線の交点の作る集合
3年前
x² 上の任意の2つの点の法線の交点の作る集合
3年前
-
 e^x上の任意の2つの点の法線の交点の作る集合
3年前
e^x上の任意の2つの点の法線の交点の作る集合
3年前
-
 e^x上の任意の2つの点の法線の交点の作る集合
3年前
e^x上の任意の2つの点の法線の交点の作る集合
3年前
-
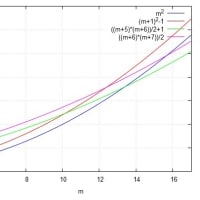 とある2つの数列 An, Bnの差が指定されたとき、最小の nを求める
4年前
とある2つの数列 An, Bnの差が指定されたとき、最小の nを求める
4年前
-
 点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
-
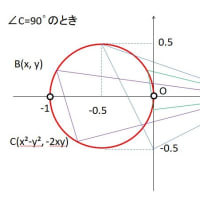 点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
-
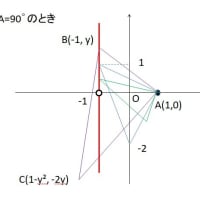 点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
-
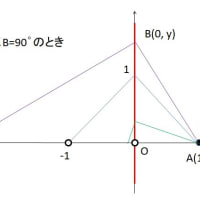 点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
「解析(極限・数列)」カテゴリの最新記事
 漸化式、a₁=2 , a[n+1]=2a[n]+2n²の解
漸化式、a₁=2 , a[n+1]=2a[n]+2n²の解 A[n+2]A[n]=A[n+1]²-1 (n≧1) , A₁=1, A₂≧2 の数列が A[n]≠0 を満たすこと
A[n+2]A[n]=A[n+1]²-1 (n≧1) , A₁=1, A₂≧2 の数列が A[n]≠0 を満たすこと 数列 a[n+1]=(1+1/n)(a[n]/2+1) , a₁=1 の収束の証明
数列 a[n+1]=(1+1/n)(a[n]/2+1) , a₁=1 の収束の証明 とある2つの数列 An, Bnの差が指定されたとき、最小の nを求める
とある2つの数列 An, Bnの差が指定されたとき、最小の nを求める aに収束する複素数の数列{a[n]}がlim[n→∞](1+a[n]/n)^n=e^aとなることの証明
aに収束する複素数の数列{a[n]}がlim[n→∞](1+a[n]/n)^n=e^aとなることの証明 lim[x→0] { (e^x-1)/x }^(1/x)=√e の証明方法
lim[x→0] { (e^x-1)/x }^(1/x)=√e の証明方法  a[n+1]=a[n]/(1+a[n]²) , a₁>0 のとき、a[n] → 0 を単調減少・有界を使わずに証明
a[n+1]=a[n]/(1+a[n]²) , a₁>0 のとき、a[n] → 0 を単調減少・有界を使わずに証明 不等式 (1/2)(3/4)(5/6)・・・{(2n-1)/2n}<1/√(3n) の証明
不等式 (1/2)(3/4)(5/6)・・・{(2n-1)/2n}<1/√(3n) の証明 数列 a[n+1]=A+C/(B+a[n]) , a₁>0 の収束の証明
数列 a[n+1]=A+C/(B+a[n]) , a₁>0 の収束の証明 数列 a[n+1]=2a+(1/a[n]) , a₁=2a の収束の証明
数列 a[n+1]=2a+(1/a[n]) , a₁=2a の収束の証明














