1.まえがき
下記の極限を級数展開やロピタルの定理を使わずに求めよ。という問題があった。
lim[x→0] { (ex-1)/x }(1/x) = √e (x≠0)・・・・・①
2.仮定
設定がよくわからないが、何かの前提を決めないと求められないはずなので
(1+1/x)x → e (x → ∞)
つまり、
(1+x)(1/x) → e (x → 0) ・・・・・・・・・②
を使う。
なお、級数展開というのはランダウの o記号を使った級数と思われる。
3.計算
まず、x → 0 なので、0 < |x| < 1 として議論してよい。
3.1 0 < x < 1 のとき
1+x+x²/2 < ex < 1+2x/(2-x) ・・・・・・・③
が成り立つ。証明は4項。すると与式から
{ 1+x/2 }(1/x) < { (ex-1)/x }(1/x) < { 2/(2-x) }(1/x)
が成り立つ。左辺は②により
{ 1+x/2 }(1/x) = { ( 1+x/2 )(2/x) }1/2 → e1/2
となる。
右辺は
{ 2/(2-x) }(1/x) = 1/{ (1-x/2)(-2/x) }-1/2 → 1/e-1/2 = e1/2
となり、挟み撃ちから、①が証明された。
3.2 -1 < x < 0 のとき
y=-x とおくと、0 < y < 1, y → 0 となる。さらに
{ (ex-1)/x }(1/x) = { (e-y-1)/(-y) }(-1/y) = 1/{ e-y(ey-1)/y }(1/y)
= e/{ (ey-1)/y }(1/y) → e/√e=√e (3.1項から)
したがって、x < 0 でも①が証明された。
以上により、x≠0 について、①が証明された。
4.不等式③の証明
1+x+x²/2 < ex (x>0) の証明は、マクローリン展開から自明だが、級数展開を使用せずと
のことなので、定石に基づき証明する。
f(x)=ex-(1+x+x²/2)
とおく。すると f(0)=0 であり、f(x) > 0 (x > 0) を示せばよい。
f'(x)=ex-(1+x) , f'(0)=0
f''(x)=ex-1 , f''(0)=0
f'''(x)=ex > 0
となる。順次、遡ると f''(x) > 0 → f'(x) > 0 → f(x) > 0 が得られた。
つぎに、ex < 1+2x/(2-x) (x>0) を証明する。
g(x)=1+2x/(2-x)-ex
とおく。すると g(0)=0 であり、同様に、g(x) > 0 (x > 0) を示せばよい。このとき
2x/(2-x)=-2+4/(2-x) なので
g'(x)=4/(2-x)²-ex , g'(0)=0
g''(x)=8/(2-x)³-ex , g''(0)=0
g'''(x)=24/(2-x)⁴-ex , g'''(0)=3/2-1=1/2
g(4)(x)=24・4/(2-x)⁵-ex , g(4)(0)=3-1=2
ここで、24・4/(2-x)⁵ > 3 , ex < 3 (x < 1) なので、g(4)(x) > 0 となり、同様に、順次、遡って
g(x) > 0 が得られる。
なお、ex < 1+2x/(2-x) の関係の導出の根拠であるが、級数展開から (x < 1 に注意して)
ex =1+x+x2/2+x3/3!+・・・+xn/n!+・・・ < 1+x+x2/2+x3/22+・・・+xn/2n-1+・・・
=1+x{1+x/2+(x/2)2+・・・+(x/2)n-1+・・・}=1+x/(1-x/2)=1+2x/(2-x)
を得る。
以上
最新の画像[もっと見る]
-
 電源や抵抗の電力が 電圧と電流の積 VIとなる理由
2年前
電源や抵抗の電力が 電圧と電流の積 VIとなる理由
2年前
-
 関数 f(x)=x²-2ax+a+2 とx軸の交点が 1<x<3 の区間に1つだけあるときの aの条件
3年前
関数 f(x)=x²-2ax+a+2 とx軸の交点が 1<x<3 の区間に1つだけあるときの aの条件
3年前
-
 x² 上の任意の2つの点の法線の交点の作る集合
3年前
x² 上の任意の2つの点の法線の交点の作る集合
3年前
-
 e^x上の任意の2つの点の法線の交点の作る集合
3年前
e^x上の任意の2つの点の法線の交点の作る集合
3年前
-
 e^x上の任意の2つの点の法線の交点の作る集合
3年前
e^x上の任意の2つの点の法線の交点の作る集合
3年前
-
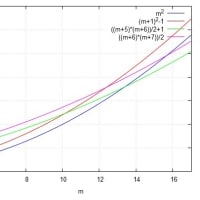 とある2つの数列 An, Bnの差が指定されたとき、最小の nを求める
4年前
とある2つの数列 An, Bnの差が指定されたとき、最小の nを求める
4年前
-
 点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
-
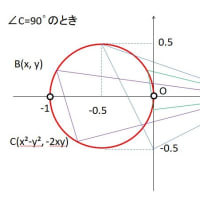 点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
-
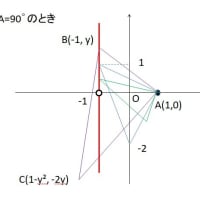 点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
-
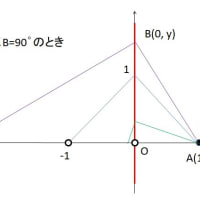 点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
点A:(1,0)と複素数 zと z² の点をB,Cとし、3角形ABCが直角3角形の時、点Bの軌跡を求む
4年前
「解析(極限・数列)」カテゴリの最新記事
 漸化式、a₁=2 , a[n+1]=2a[n]+2n²の解
漸化式、a₁=2 , a[n+1]=2a[n]+2n²の解 A[n+2]A[n]=A[n+1]²-1 (n≧1) , A₁=1, A₂≧2 の数列が A[n]≠0 を満たすこと
A[n+2]A[n]=A[n+1]²-1 (n≧1) , A₁=1, A₂≧2 の数列が A[n]≠0 を満たすこと 数列 a[n+1]=(1+1/n)(a[n]/2+1) , a₁=1 の収束の証明
数列 a[n+1]=(1+1/n)(a[n]/2+1) , a₁=1 の収束の証明 とある2つの数列 An, Bnの差が指定されたとき、最小の nを求める
とある2つの数列 An, Bnの差が指定されたとき、最小の nを求める aに収束する複素数の数列{a[n]}がlim[n→∞](1+a[n]/n)^n=e^aとなることの証明
aに収束する複素数の数列{a[n]}がlim[n→∞](1+a[n]/n)^n=e^aとなることの証明 lim[x→0] { (e^x-1)/x }^(1/x)=√e の証明方法
lim[x→0] { (e^x-1)/x }^(1/x)=√e の証明方法  a[n+1]=a[n]/(1+a[n]²) , a₁>0 のとき、a[n] → 0 を単調減少・有界を使わずに証明
a[n+1]=a[n]/(1+a[n]²) , a₁>0 のとき、a[n] → 0 を単調減少・有界を使わずに証明 不等式 (1/2)(3/4)(5/6)・・・{(2n-1)/2n}<1/√(3n) の証明
不等式 (1/2)(3/4)(5/6)・・・{(2n-1)/2n}<1/√(3n) の証明 数列 a[n+1]=A+C/(B+a[n]) , a₁>0 の収束の証明
数列 a[n+1]=A+C/(B+a[n]) , a₁>0 の収束の証明 数列 a[n+1]=2a+(1/a[n]) , a₁=2a の収束の証明
数列 a[n+1]=2a+(1/a[n]) , a₁=2a の収束の証明














