このブログで,「のぼしぇもん」さんから,まっとうな12音平均律で純正律のように響く楽器はできないのか,というコメントをいただいたことがある.
そういう平均律を計算機で作るのは可能である.おそらく最初にこの問題に挑戦したのは,村上陽一郎訳「音楽の科学」の著者,ジョン・R・ピアースであろう.
響きが良いというのは,倍音同士の周波数が一致するからである.たとえば純正律では,ドの3倍波とソの2倍波の周波数は一致するので,ドとソの響きは良い.
12音平均律では音の高さは等比数列をなし,その公比は2の1/12乗である.公比が無理数だから,一筋縄ではいかない.
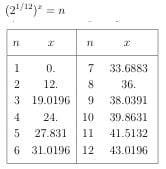
そこで,平均律の構成音の倍音の周波数を多少ずらすことにする.平均律において,根音から数えてx 番目の音が第n 倍音に一致するなら,x はこのカットの先頭の方程式を満たすはずである.倍音の倍数 n を決めたときの x が表になっている.
x は何番目という序数の指標だから整数でなければならない.そこでこの表に最も近い整数を採用し,その周波数を倍音もどきの周波数とすることにする.
こうして周波数位置にピークを持つ音源をソフトウェアで作る.
この項 未完です.
そういう平均律を計算機で作るのは可能である.おそらく最初にこの問題に挑戦したのは,村上陽一郎訳「音楽の科学」の著者,ジョン・R・ピアースであろう.
響きが良いというのは,倍音同士の周波数が一致するからである.たとえば純正律では,ドの3倍波とソの2倍波の周波数は一致するので,ドとソの響きは良い.
12音平均律では音の高さは等比数列をなし,その公比は2の1/12乗である.公比が無理数だから,一筋縄ではいかない.
そこで,平均律の構成音の倍音の周波数を多少ずらすことにする.平均律において,根音から数えてx 番目の音が第n 倍音に一致するなら,x はこのカットの先頭の方程式を満たすはずである.倍音の倍数 n を決めたときの x が表になっている.
x は何番目という序数の指標だから整数でなければならない.そこでこの表に最も近い整数を採用し,その周波数を倍音もどきの周波数とすることにする.
こうして周波数位置にピークを持つ音源をソフトウェアで作る.
この項 未完です.

























おおおお、あちきも多少は役に立っているのか ?
。。。と思ったら、
きっと DGB さんの影響ですな ^_^;
-- この方、相当な達人ですなあ。。。
続編に期待しております。
おっしゃるように,DGB さんのHPにはまってしまいました.
私はといえば,暇なはずなのになんだか忙しい状態です.
このブログについてはlogなんか使うな,というご意見もいただいてしまいました.
方程式の解がlogになり,それを数値で書くと表のようになります.
でも,方程式等使わずに直感的に言えば,「平均律でオクターブなり2オクターブなり上のミやソの高さにドの倍音もどきを作る」ということになります.