今回からは、JASPの「Frequencies」に入ります。
ここでは、JASPによる分割表形式での統計的検定についてご紹介します。
ここでは、JASPによる分割表形式での統計的検定についてご紹介します。
同書45ページの「表5.7 フイッシャー計算の分割表」を下記(表1)の様なデータ・フォームにし、今までと同様にExcel(CSV形式)で保存して下さい。
表1 分割表形式のデータ・フォーム(Medicine→Gender と訂正、以下同じ)

例えば、「Frequency.csv」として保存されたなら、
JASP起動→「Frequency.csv」の読込み
↓
Frequencies→Contingency Tables
↓
図1 変数の選択
↓
Frequencies→Contingency Tables
↓
図1 変数の選択
図2 出力結果(1)
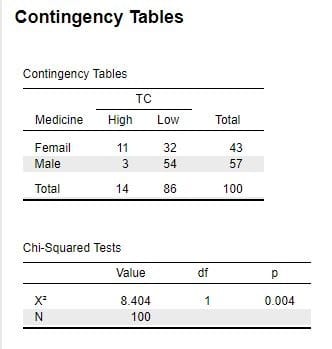
「Chi-squared=8.404、p=0.004」となっていますが、
ここで、
図3の様に検定方法を追加してみます。
図3の様に検定方法を追加してみます。
図3 検定方法の追加

赤矢印にチェックを入れ選択してみましょう。
図4 出力結果(1)
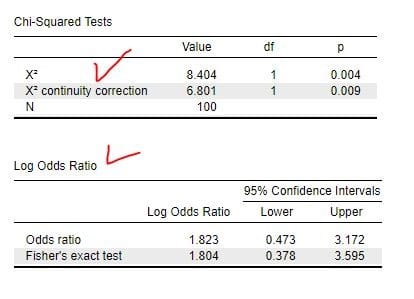
Ci-Squared Test の ”Chi continuity correction” はYates の補正値の値となります(赤矢印)。
また、
対数オッズ比(赤矢印)は、
Log Odds ratio=1.823(0.473~3.172)
Fisher's exact test の Log Odds ratio=1.804(0.378~3.595)
対数オッズ比(赤矢印)は、
Log Odds ratio=1.823(0.473~3.172)
Fisher's exact test の Log Odds ratio=1.804(0.378~3.595)
・・・となっています。
対数オッズ比はオッズ比の自然対数値のことで、ロジスティック回帰分析の係数にあたり、その指数がオッズ比になります。
オッズ比が知りたいなら、
データ解析環境「R」で次のようにすれば良いでしょう。
例えば、
データ解析環境「R」で次のようにすれば良いでしょう。
例えば、
「Frequency.csv」を Excelで開き、データ部分をすべて選択しコーピーすればグリッドボードにコピーされますので、
事前に「R」の "R Console" に下記のコマンドを書いておき実行して下さい。
事前に「R」の "R Console" に下記のコマンドを書いておき実行して下さい。
dat<- read.delim("clipboard", header=T) ←事前に「R」の"R Console"に記載しておき実行する。
↓ ここから以下は、新しいスクリプトに記載して実行すると良いでしょう。
dat
fit <- glm(Medicine ~ TC, weights = Count, data = dat, family = binomial)
summary(fit)
fit <- glm(Medicine ~ TC, weights = Count, data = dat, family = binomial)
summary(fit)
図5 出力結果(2)

TCLow の Estimate(1.8225) は、図4の出力結果(1)の "Log Odds Ratio" と一致します。
ここで、
次の「R」コマンドを実行すると、Odds ratio とその95%信頼限界を求めることが出来ます。
次の「R」コマンドを実行すると、Odds ratio とその95%信頼限界を求めることが出来ます。
***
fit <- glm(Medicine ~ TC, weights = Count, data = dat, family = binomial)
summary(fit)
Odds<- exp(summary(fit)$coef["TCLow",1])
Odds
OddsCI<- exp(summary(fit)$coef["TCLow",1] +
qnorm(c(0.025, 0.975)) * summary(fit)$coef["TCLow",2])
OddsCI
fit <- glm(Medicine ~ TC, weights = Count, data = dat, family = binomial)
summary(fit)
Odds<- exp(summary(fit)$coef["TCLow",1])
Odds
OddsCI<- exp(summary(fit)$coef["TCLow",1] +
qnorm(c(0.025, 0.975)) * summary(fit)$coef["TCLow",2])
OddsCI
出力結果:
オッズ比(Odds)
[1] 6.1875
オッズ比(Odds)
[1] 6.1875
Odds ratio の95%信頼限界(OddsCI)
[1] 1.60503 23.85323
***
[1] 1.60503 23.85323
***
以上によりOdd ratioとその CIを求められます(Excelでの筆算でも良いでしょう)。
なお、
Fisher's exact test のp値(両側)を知りたいなら、次により求められます。
なお、
Fisher's exact test のp値(両側)を知りたいなら、次により求められます。
***
Tab <- matrix(c(11,32,3,54), byrow=T, nc=2)
fisher.test(Tab, alternative="t")
Tab <- matrix(c(11,32,3,54), byrow=T, nc=2)
fisher.test(Tab, alternative="t")
出力結果:
図6 fisher.test の結果

図6 fisher.test の結果

***










