
炭素繊維を吊るす木製のフロートをデザインしていた頃、平面の分割に興味を持っていました。三角形・四角形・六角形による平面の分割(逆に言えば充填)はそれほど面白くありません。三角形は凸な図形しかありませんが、四角形以上の多角形は凹んだ図形を描くことが出来ます。凸でない、凹んだ四角形でも平面を充填出来ることが面白いと思いました。
やはり研究者の興味を引くのは凸五角形のようで、「充填凸五角形とそのタイル張り模様の系統的研究」という論文には以下のような記述がありました。
凸五角形の充填形は,現在までに14 種類に表現されている.これで網羅という証明はなく,科学的アプローチとして試みるべきことがなされていない唯一未解決問題である。
素人でも理解できる幾何学の問題ですが、難関らしいですね。凸であると言う条件を外すとどうなるのでしょうか?あの頃、CADで色々遊んでいた発見したのが冒頭のパターンでした。作り方は簡単で、出発点は正五角形です。
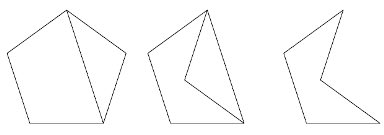
まずCADで辺(エッジ)を決めて正五角形を作図します。一つ置いた頂点を結んだ線分を引き、この線分を基準として、2辺を複写します。鏡像ですね。先ほどの線分と2辺を削除して、凹5角形が出来上がります。これをブロックで定義して、次々に複写・回転をすれば、この凹んだ5角形で平面を隙間無く埋め尽くすことが出来るのです。
このタイル張りのパターンを最初に発見したのは私かどうか分かりません。私は愛好者であって研究者ではないからです。でも錆び付いたCADのスキルに油を差して、また何か発見したいと願っています。
↓ポチッと応援お願いします!

やはり研究者の興味を引くのは凸五角形のようで、「充填凸五角形とそのタイル張り模様の系統的研究」という論文には以下のような記述がありました。
凸五角形の充填形は,現在までに14 種類に表現されている.これで網羅という証明はなく,科学的アプローチとして試みるべきことがなされていない唯一未解決問題である。
素人でも理解できる幾何学の問題ですが、難関らしいですね。凸であると言う条件を外すとどうなるのでしょうか?あの頃、CADで色々遊んでいた発見したのが冒頭のパターンでした。作り方は簡単で、出発点は正五角形です。

まずCADで辺(エッジ)を決めて正五角形を作図します。一つ置いた頂点を結んだ線分を引き、この線分を基準として、2辺を複写します。鏡像ですね。先ほどの線分と2辺を削除して、凹5角形が出来上がります。これをブロックで定義して、次々に複写・回転をすれば、この凹んだ5角形で平面を隙間無く埋め尽くすことが出来るのです。
このタイル張りのパターンを最初に発見したのは私かどうか分かりません。私は愛好者であって研究者ではないからです。でも錆び付いたCADのスキルに油を差して、また何か発見したいと願っています。
↓ポチッと応援お願いします!



























あおおにさんの作品も拝見しました。Pentalbiも概要が分かりました。
http://www.albinegri.ch/cff_1.htm
教えて頂いてありがとうございます。
この製品は1980年に特許申請されていますので、現在では特許も切れているはずです。
単純な形状ながら、平面を隙間無く埋め尽くすので色んな応用が考えられますね。
昨年、世紀の大傑作ができたと思い、百町森というおもちゃ店の相沢康夫氏(naefのおもちゃ作家)に見せたら1980年に作品化されてました。
Pentalbiという名前でNAEF AGというスイスのメーカーからM.Gubeliという人が発表してます。
渦巻き(スパイラル)幅が同じなのでアルキメデス螺旋と言えなくはないでしょうね。
同じ凹5角形を使って異なる張り方があるように思います。誰か挑戦してみませんか?
外中比をφとすれば、a=φ/(2π)になりますね。一周して伸びる径がφになる。
アルキメデス螺旋になっていきますよね。
アルキメデス螺旋は、曲座標で表すとr=aθ。
でこのaですが、元になった正五角形の1辺の長さを1とすると、aは1.61803・・・。外中比、俗に言う黄金比になっていますね。
いやいやなかなか興味深い。