だいぶ間が開いたけど、「すぐに役立つ統計のコツ」(第6章)では"相関と回帰"の手法を紹介しています。
今回は、
医学・生物学などの実験や臨床検査の現場でよく用いられる検量線について、ご紹介しましょう。
本書の83ページの"4. 臨床検査で大切な検量線"を見て下さい。通常、
検量線は校正直線(曲線)と呼ばれ、標準物質濃度(x)に対応する分光光度計などの吸光度(y)を、グラフ用紙の横軸(x)と濃度を縦軸(y)にプロットし、測定物質の未知の吸光度(y0)を読み取り、未知物質の濃度(x0)を求めます。こでは昔のことです。
現在では、
xとyの直線(曲線)回帰式、例えば、y=aⅹ + b(1次方程式) や y=aⅹ^2+bⅹ+c(2次方程式) を使い、吸光度(y0)を知って濃度(x0)をパソコンなどで推定します。これを回帰式からの逆推定と言います。
これは、
回帰式が「ⅹを基準にyを回帰するので、回帰誤差はyの方にである」からです。
現在では、
xとyの直線(曲線)回帰式、例えば、y=aⅹ + b(1次方程式) や y=aⅹ^2+bⅹ+c(2次方程式) を使い、吸光度(y0)を知って濃度(x0)をパソコンなどで推定します。これを回帰式からの逆推定と言います。
これは、
回帰式が「ⅹを基準にyを回帰するので、回帰誤差はyの方にである」からです。
それでは、
MS-Excelで実際に例題を使ってやって見ましょう。
MS-Excelで実際に例題を使ってやって見ましょう。
血清中の総コレステロール値を測定する場合、
標準物質(既知濃度のもの)を倍々希釈などして、図1の様な濃度(ⅹ)と吸光度(y)が得られたとします(図1)。
標準物質(既知濃度のもの)を倍々希釈などして、図1の様な濃度(ⅹ)と吸光度(y)が得られたとします(図1)。
図1 コレステロールの濃度(x)と吸光度(y)

図1の緑色セル部分をクリックし、「挿入→グラフ→散布図→散布図」で図2の散布図を得ることが出来ます。
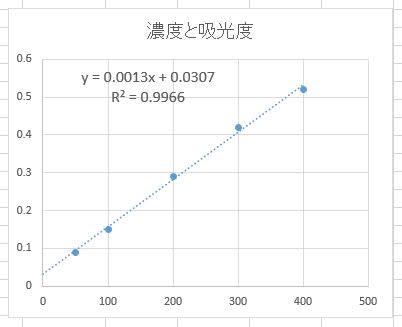
図2 濃度(x)と吸光度(y)の散布図と近似直線
そして、
図2のプロットのどれかを、「右クリック→近似曲線の追加→近似曲線のオプション:
[直線近似◎、グラフに数式を表示する◎、グラフにR-2乗値を表示する◎]→[×](終了)]
図2のプロットのどれかを、「右クリック→近似曲線の追加→近似曲線のオプション:
[直線近似◎、グラフに数式を表示する◎、グラフにR-2乗値を表示する◎]→[×](終了)]
とすれば、
図2の様な近似直線が得られます。盲検(ブランク)をとれば原点近くを通る直線となります。
ここで、
直線回帰式は 吸光度(y)=0.0013×濃度(ⅹ)+0.0307 となりますので、その解はⅹ0=(y0-0.0307)/0.0014 となります。
図2の様な近似直線が得られます。盲検(ブランク)をとれば原点近くを通る直線となります。
ここで、
直線回帰式は 吸光度(y)=0.0013×濃度(ⅹ)+0.0307 となりますので、その解はⅹ0=(y0-0.0307)/0.0014 となります。
よって、
未知吸光度y0=0.42 の濃度はⅹ0=299.5 と逆推定出来ます。
未知吸光度y0=0.42 の濃度はⅹ0=299.5 と逆推定出来ます。
検量線は曲線である場合も多々あります。
本書の85ページの上段にある「濃度と吸光度」を使って見ましょう。
図3 濃度(x)と吸光度(y)のデータ
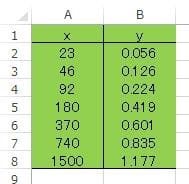
図3の緑色セル部分をクリックし、同様の方法で図4の様な散布図を作ります。
図4 濃度(x)と吸光度(y)の散布図と近似曲線

図4の回帰式は、
y=aⅩ^2+bⅩ+c=(-5E-07)・Ⅹ^2+0.0015・Ⅹ+0.084
ですので、
この2次方程式の解から、未知吸光度(y0)に対する濃度(ⅹ0)の逆推定は、
ⅹ0=(-b±√(b^2-4a(c-y0))/(2a)
この2次方程式の解から、未知吸光度(y0)に対する濃度(ⅹ0)の逆推定は、
ⅹ0=(-b±√(b^2-4a(c-y0))/(2a)
です。よって、
未知吸光度 y0=0.024 のとき、
Ⅹ0=(-0.0015+√(0.0015^2-4*-0.0000005*(0.084-0.224)))/(2*-0.0000005)=96.4
となります。
検量線としては当てはめがあまり良くありませんので、別の関数へのあてはめを検討する必要がありそうです。
対数変換による当てはめは「すぐに役立つ統計のコツ」(85ページ)を見て下さい。
本書の記載(校正)ミスの訂正は"情報統計研究所"(TOPページ)の「新刊書紹介(正誤表あり)」にあります。
本書の記載(校正)ミスの訂正は"情報統計研究所"(TOPページ)の「新刊書紹介(正誤表あり)」にあります。
***
訂正:
訂正:
本書(85ページ)の常用対数変換濃度は次の次の通り訂正します。
1.362, 1.663, 1.964, 2.255, 2.568, 2.869, 3.176
1.362, 1.663, 1.964, 2.255, 2.568, 2.869, 3.176
***
なお、
「R」の環境があれば、もっと簡単に詳しい情報を得ることが出来ます。それは、次回にご紹介したいと思います。
「R」の環境があれば、もっと簡単に詳しい情報を得ることが出来ます。それは、次回にご紹介したいと思います。
次回は、
「R」による2次曲線からの逆推定です。
「R」による2次曲線からの逆推定です。
情報統計研究所はここから!


















