司馬さん、というと皆さん誰を思い浮かべますか?司馬遼太郎さん、でしょうか?私の場合は、なんと言っても司馬遷なのです。司馬遷と言うのは、紀元前100年ごろの中国の歴史家で、史記という歴史書を書き残した人です。
こう言うと、何だかインテリぽくってキザに聞こえるかもしれませんが、20才の時にたまたま司馬遷の史記を読んだことが、私のその後の人生に大きな影響を与えたました。人生に悩むと普通は宗教に走りますが、私の場合は歴史書などのノンフィクションやドキュメンタリから指針を受けることが性に合っていることを発見したのは実にこの本でした。
ご存知のことと思いますが、司馬遷の史記というのは、中国文明の最初、つまり今から3000年ほど前、から紀元前100年ごろまでの歴史を描いたものです。
ところで私は中学校から高校、大学の教養部(2年生)にかけて、典型的な理科系人間でした。つまり英語を除いては、文科系の科目、とりわけ歴史などは、世界史、日本史ともどちらもあじけない歴史的語句の羅列に過ぎないと思い込んでいました。
ところが、史記を初めて読んでから世の中の見方が非常に変わりました。一言で言うと、『恥ずかしい生き方をしてはいけない』と言う事を知ったことです。この『恥ずかしい生き方』というのは私はこのように受け止めました。人は他人にはウソはつけても、自分自身にはウソはつけないでしょう。つまり、『恥ずかしい生き方をしない』ということは自分自身の生き方を振り返って、『ああいうことをしなかったら、良かったのに!』と悔いの残る事はしないことなのです。説苑という本にも『行いは、悔いなきより大なるはなし』と同じ趣旨の言葉があります。
史記は全編とは言いませんが、そういう『まっとうな』生き方をした人が活き活きと描かれています。吉田松陰や伊藤博文など、幕末、明治初期の志士たちは必ずといって良いほど史記から多大な影響、励ましを受けています。皆さんも一度、さわりの部分でも結構ですから史記を読んでみてはいかがですか?必ず世界観や人生の見方が変わるはずです。
この史記のなかでもとりわけ精彩あふれる章が『項羽と劉邦』の部分でしょう。項羽の軍は負けがこんで、とうとう敵(漢軍)に囲まれた時に敵の漢軍からは自分の故郷の楚の歌声が聞こえてくる、つまり、味方はすべて敵に下った、というのが有名な『四面楚歌』です。その夜、項羽は今生の別れに美女の虞美人を前にして、短い生涯(30歳)最後の舞を舞う姿などは、実に悲劇的情緒たっぷりです。翌朝は最後の突撃をするも遂には逃げ場所がなくなり、自害して果てます。このように項羽は最後の最後まで、劉邦の最大のライバルだったのですが、劉邦は項羽の遺体を非常に手厚く葬っています。私が中国の歴史で感心する点は、敵でも立派な人は高く評価している事です。
それから200年後、前漢が王莽によって滅ぼされましたがすぐまた、光武帝によって再興されます。これが後漢です。光武帝(劉秀)と言う人は、いわゆる豪傑肌の英雄でなかったようです。帝位についた後、親戚中をあつめたパーティでは、親戚のおばさん達は一様に、『あの引っ込み思案の秀ちゃんがねえ~』とびっくりしたと言われています。
この劉秀が若いころ街中で評判の美人の陰麗華(いん・れいか)を見て是非出世して彼女を娶りたいものだと強く思ったのでした。帝位につくや真っ先にその念願を果たしたということです。
さて、私達が小学校のころは1ヶ月に1回、席替えがありました。随分昔のことなので記憶が定かではありませんが、席の場所は確かくじ引きだったように思えます。この時は、いつも子供心にどきどきしたものでした。劉秀の麗華ほどの思い入れはありませんが、やはり好きな女の子の隣に座れるかどうかは重大な関心事でした。一方、嫌いなヤツからは離れられるか、と。とにかく、席替えは秘かに手に汗を握る波乱に満ちた一編のドラマであったのでした。 誰でも、経験はあると思いますが、席替えの後では、必ず何らかの不満はのこるものです。誰もが皆満足できる席替えというのはなかなか難しいものです。
さて今回は、皆の満足度が一番高くなる席替えを自動的に見つける方法を考えて見ましょう。このような問題、つまりある条件下で最善の解を見つける方法を、『制約条件下の最適化問題』と言います。
この席替えのケースをとって説明しましょう。
先ず、クラス全員に紙を配って、満足度のアンケートを取ります。各自に他人を5段階で評価してもらいます。(1=大好きが、5=大嫌い)AさんのBさんに対する評価はその逆の評価とは一般的には必ずしも一致しませんので、ここでは便宜的に2人の互いの相性というのは、2人の平均値と定義します。

図1:クラス8人(A-H)の相性の表(対象行列の左下部のみ表示)
このようにすると、相性は対称行列になります。(対角線に対称な項が同じ値をとる。)
さて、この表の値を使って合理的な席の位置を決めるには、多次元尺度法という方法を使います。多次元尺度法というのは、データが主観的な観点で評点化されているアンケートデータのような場合のデータ解析には、よく使われる手法です。また職種や出身県のようなカテゴリーデータのようなお互いの関係を計測できない(専門用語では、測度を導入できない)データ群については類似度で分類することができます。
多次元尺度法にもいろいろとありますが、今回はSammon Mapという方法を使って解きました。この手法の詳しいことは、下記に掲げてありますURLなどをご参照下さい。
席替えの場合には、次のような手順となります。
【1】まず最初に席の配置を適当に決めます。この時は相性表を全く無視しています。
【2】その配置で、互いの席の離れ具合の表を作ります。具体的には2人つづをペアーとして距離を計算します。その距離を相性表と同じ土俵で比較できるようにする為に、距離の値を調整します。今回のケースでは、最短距離を相性表の一番小さい値、すなわち1に変え、最遠距離を相性表の一番大きい値、すなわち5に変えます。
【3】調整された距離と相性表の値の差分の二乗和、つまり、全体の誤差を計算します。その誤差を元にして、席の配置をどの方向にちょっとずらせば誤差が少なくなるかを計算します。(専門用語では偏微分をとるといいます。)
【4】席の配置を【3】で計算された方向にちょっとずつずらします。この操作によって全体の誤差が少し減少するはずです。その後再度【2】に戻って誤差の計算をして、また席をすこしずらします。
【5】このようにして、誤差が一番小さくなるまで席をすこしづつずらしていきます。
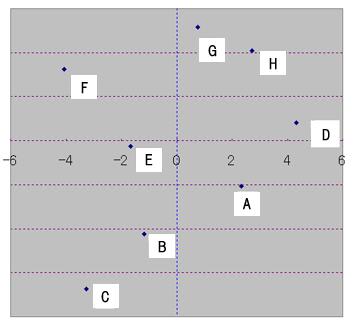
図2:クラス8人(A-H)の席の配置
このようにして求められた席の位置(図2)と相性の表(図1)を比べますと、必ずしも席の全てのペアが相性の値の順序と完全には一致していませんが、全体としてみると大体あっているのが分かるでしょう。
このように多次元尺度法を使うと、数値化しにくい属性の類似度をベースにして、互いの関係を図に表すことができます。世の中の社会系・人文系のデータでは、数値化し難くく、かつ主観的なデータが多いですので、ぜひそのような場合には今回ご紹介しました多次元尺度法を活用してみて下さい。
【参考】Sammon Mapに関する情報は下記をごらん下さい。
【1】Sammon, J. 1969.
"A nonlinear mapping for data structure analysis", IEEE Trans. Comput. 18.
【2】Agrafiotis, D.K., 1997
"A new method for analyzing protein sequence relationships based on Sammon maps", Protein Sci. 1997 6: 287-293
【3】Golden, B.L., 2001
"An Example of Visualization in Data Mining",
http://www.rhsmith.umd.edu/faculty/bgolden/recent_presentation_ppt_links/2001visualizationdatamining.ppt
続く...
こう言うと、何だかインテリぽくってキザに聞こえるかもしれませんが、20才の時にたまたま司馬遷の史記を読んだことが、私のその後の人生に大きな影響を与えたました。人生に悩むと普通は宗教に走りますが、私の場合は歴史書などのノンフィクションやドキュメンタリから指針を受けることが性に合っていることを発見したのは実にこの本でした。
ご存知のことと思いますが、司馬遷の史記というのは、中国文明の最初、つまり今から3000年ほど前、から紀元前100年ごろまでの歴史を描いたものです。
ところで私は中学校から高校、大学の教養部(2年生)にかけて、典型的な理科系人間でした。つまり英語を除いては、文科系の科目、とりわけ歴史などは、世界史、日本史ともどちらもあじけない歴史的語句の羅列に過ぎないと思い込んでいました。
ところが、史記を初めて読んでから世の中の見方が非常に変わりました。一言で言うと、『恥ずかしい生き方をしてはいけない』と言う事を知ったことです。この『恥ずかしい生き方』というのは私はこのように受け止めました。人は他人にはウソはつけても、自分自身にはウソはつけないでしょう。つまり、『恥ずかしい生き方をしない』ということは自分自身の生き方を振り返って、『ああいうことをしなかったら、良かったのに!』と悔いの残る事はしないことなのです。説苑という本にも『行いは、悔いなきより大なるはなし』と同じ趣旨の言葉があります。
史記は全編とは言いませんが、そういう『まっとうな』生き方をした人が活き活きと描かれています。吉田松陰や伊藤博文など、幕末、明治初期の志士たちは必ずといって良いほど史記から多大な影響、励ましを受けています。皆さんも一度、さわりの部分でも結構ですから史記を読んでみてはいかがですか?必ず世界観や人生の見方が変わるはずです。
この史記のなかでもとりわけ精彩あふれる章が『項羽と劉邦』の部分でしょう。項羽の軍は負けがこんで、とうとう敵(漢軍)に囲まれた時に敵の漢軍からは自分の故郷の楚の歌声が聞こえてくる、つまり、味方はすべて敵に下った、というのが有名な『四面楚歌』です。その夜、項羽は今生の別れに美女の虞美人を前にして、短い生涯(30歳)最後の舞を舞う姿などは、実に悲劇的情緒たっぷりです。翌朝は最後の突撃をするも遂には逃げ場所がなくなり、自害して果てます。このように項羽は最後の最後まで、劉邦の最大のライバルだったのですが、劉邦は項羽の遺体を非常に手厚く葬っています。私が中国の歴史で感心する点は、敵でも立派な人は高く評価している事です。
それから200年後、前漢が王莽によって滅ぼされましたがすぐまた、光武帝によって再興されます。これが後漢です。光武帝(劉秀)と言う人は、いわゆる豪傑肌の英雄でなかったようです。帝位についた後、親戚中をあつめたパーティでは、親戚のおばさん達は一様に、『あの引っ込み思案の秀ちゃんがねえ~』とびっくりしたと言われています。
この劉秀が若いころ街中で評判の美人の陰麗華(いん・れいか)を見て是非出世して彼女を娶りたいものだと強く思ったのでした。帝位につくや真っ先にその念願を果たしたということです。
さて、私達が小学校のころは1ヶ月に1回、席替えがありました。随分昔のことなので記憶が定かではありませんが、席の場所は確かくじ引きだったように思えます。この時は、いつも子供心にどきどきしたものでした。劉秀の麗華ほどの思い入れはありませんが、やはり好きな女の子の隣に座れるかどうかは重大な関心事でした。一方、嫌いなヤツからは離れられるか、と。とにかく、席替えは秘かに手に汗を握る波乱に満ちた一編のドラマであったのでした。 誰でも、経験はあると思いますが、席替えの後では、必ず何らかの不満はのこるものです。誰もが皆満足できる席替えというのはなかなか難しいものです。
さて今回は、皆の満足度が一番高くなる席替えを自動的に見つける方法を考えて見ましょう。このような問題、つまりある条件下で最善の解を見つける方法を、『制約条件下の最適化問題』と言います。
この席替えのケースをとって説明しましょう。
先ず、クラス全員に紙を配って、満足度のアンケートを取ります。各自に他人を5段階で評価してもらいます。(1=大好きが、5=大嫌い)AさんのBさんに対する評価はその逆の評価とは一般的には必ずしも一致しませんので、ここでは便宜的に2人の互いの相性というのは、2人の平均値と定義します。

図1:クラス8人(A-H)の相性の表(対象行列の左下部のみ表示)
このようにすると、相性は対称行列になります。(対角線に対称な項が同じ値をとる。)
さて、この表の値を使って合理的な席の位置を決めるには、多次元尺度法という方法を使います。多次元尺度法というのは、データが主観的な観点で評点化されているアンケートデータのような場合のデータ解析には、よく使われる手法です。また職種や出身県のようなカテゴリーデータのようなお互いの関係を計測できない(専門用語では、測度を導入できない)データ群については類似度で分類することができます。
多次元尺度法にもいろいろとありますが、今回はSammon Mapという方法を使って解きました。この手法の詳しいことは、下記に掲げてありますURLなどをご参照下さい。
席替えの場合には、次のような手順となります。
【1】まず最初に席の配置を適当に決めます。この時は相性表を全く無視しています。
【2】その配置で、互いの席の離れ具合の表を作ります。具体的には2人つづをペアーとして距離を計算します。その距離を相性表と同じ土俵で比較できるようにする為に、距離の値を調整します。今回のケースでは、最短距離を相性表の一番小さい値、すなわち1に変え、最遠距離を相性表の一番大きい値、すなわち5に変えます。
【3】調整された距離と相性表の値の差分の二乗和、つまり、全体の誤差を計算します。その誤差を元にして、席の配置をどの方向にちょっとずらせば誤差が少なくなるかを計算します。(専門用語では偏微分をとるといいます。)
【4】席の配置を【3】で計算された方向にちょっとずつずらします。この操作によって全体の誤差が少し減少するはずです。その後再度【2】に戻って誤差の計算をして、また席をすこしずらします。
【5】このようにして、誤差が一番小さくなるまで席をすこしづつずらしていきます。

図2:クラス8人(A-H)の席の配置
このようにして求められた席の位置(図2)と相性の表(図1)を比べますと、必ずしも席の全てのペアが相性の値の順序と完全には一致していませんが、全体としてみると大体あっているのが分かるでしょう。
このように多次元尺度法を使うと、数値化しにくい属性の類似度をベースにして、互いの関係を図に表すことができます。世の中の社会系・人文系のデータでは、数値化し難くく、かつ主観的なデータが多いですので、ぜひそのような場合には今回ご紹介しました多次元尺度法を活用してみて下さい。
【参考】Sammon Mapに関する情報は下記をごらん下さい。
【1】Sammon, J. 1969.
"A nonlinear mapping for data structure analysis", IEEE Trans. Comput. 18.
【2】Agrafiotis, D.K., 1997
"A new method for analyzing protein sequence relationships based on Sammon maps", Protein Sci. 1997 6: 287-293
【3】Golden, B.L., 2001
"An Example of Visualization in Data Mining",
http://www.rhsmith.umd.edu/faculty/bgolden/recent_presentation_ppt_links/2001visualizationdatamining.ppt
続く...
















