以前私は製造業の会社に入社した当初減速機(平たく言うと歯車・ギアなどを使ってモーターの回転速度を減らす機械)の新企画を担当していました。その事業部は名古屋の近くにあり、精機事業部と言っていました。新入社員が揃って名古屋に飲みに行くときなど、電車の中で、会社の話しをするのですが、別の事業部に配属された人が、『最近、お前ところのセイキはどうだ。元気か?』などと大きな声で尋ねます。そうすると、周りの一般乗客は一瞬ドキッとした表情で、なんと非常識な社員!という目でこちらを睨むのです。しかし話をしている当人たちは『セイキ』は当然『精機事業部』のことと理解しているので、そのような視線には気づかず、『セイキが弱ると、こっちまでたまらんなあ~。』などとまたまた刺激的なことを口走るといった風でした。この醜聞が原因かどうか分かりませんが、その後暫くして『セイキ』事業部は標準機械事業本部という何の変哲もない名前に改称されたのでした。
さて、セイキは漢字では、精機、性器だけでなく、世紀、正規、生起、などいろいろあります。しかしこのエッセー『数財探掘』がテーマとしているデータ解析ではセイキといえば当然『正規』という漢字を思い浮かべるはずです。またこれはガウスが発見したので、ガウシアン分布(Gaussian Distribution)とも言われます。
皆さんも高校で確率分布の代表として、綺麗な釣鐘状の正規分布を習ったことがあるでしょう。数式的に言えば、指数関数なので扱いやすい関数です。またいろいろな式変形も華麗で、魅惑的な関数です。そのうち、なんとなく、分布といえば全てが正規分布であるのが当然であるような錯覚に陥ってしまう人が多いようです。
これはある程度正しい感覚でしょう。特に自然界の現象を測定してみると正規分布が至るところでみることが出来ます。例えば、ある特定のグループの人間の身長や体重などの分布はそうでしょう。正規分布は背後に自然界の物理的・生物的な法則が厳然として存在している場合にかなり多く見られるものです。
このように、正規分布が多く使われているために誤解が発生しています。この話をしましょう。大数の法則と中心極限定理(central limit theorem)は確率論ではよく使われる概念です。
まず大数の法則の意味するところは至って簡単です。つまり、『たくさんサンプルをとるとその平均値は本来の値に近づくと』ということです。例えば野球選手の打率を考えてみましょう。たとえイチロウのような選手でも一試合だけを見ると全く打てないときもあるわけですから、3割打者といえども6回の打席で必ずヒットを2回打てるとは限りません。しかし120打席以上であれば40回以上のヒットは必ず打てるのです。つまり、打席の回数が多くなれば、イチロウ本来の打率に相当するだけのヒットは出るわけです。これが大数の法則といわれるものです。
このような簡単なことでも法則となって数式などを使って説明されると、なんとなく難しく感じて本来的な意味が分からなくなってしまうようです。数学が苦手な人は数式に惑わされてその数式が意図するところを理解しようとせずにあきらめてしまうのが原因のように私には思えます。一度、数式を離れて、普通の言葉でそれがどのような意図、意味を持ったものなのかを考えてから、数式を眺めると、意味あいが納得できるでしょう。喩えていえば、カラオケでは日本語の歌は意味が分かるので、しっかり歌えますが、英語の歌はリズムはわかるものの文の意味が分からないので歌えないことが多いものです。しかし、ディスプレイで文が表示されるとつづりと意味が分かるので結構歌えるでしょう。数式の理解もこの要領です。自分の身近な世間的な例と比較しながら、考えると数式も比較的易しく理解できるものなのです。
もう一つの中心極限定理も統計データ処理によく使われる概念ですが世間ではよく誤解されてます。その誤解とは、『サンプルを数多くを取ると結局その分布は正規分布で表現できる』というものです。つまりサンプル数が少ないときは色々な分布を示していても、サンプル数を大きくすると本来の分布である正規分布に収束していく、と言うものです。
もしこれが正しいならば、正規分布一つがあれば全ての現象が表現できることになるはずですね。統計を学ばなくても、これはどこかおかしい!と感じるはずですが、統計を学んだはずの人の中にも、これを堂々と主張する人がいるのは驚きを通り越して、あきれます。統計というと数式がいくつも出てきて難しそうに見えますがたいていは一般常識で考えられる範囲の事を数式化したに過ぎないものだと私は思っています。
それでは、中心極限定理は正しくはどう解釈すべきでしょうか?その鍵は『平均値』という語句にあります。つまり中心極限定理とは正しくは次のように次のような意味です。『サンプルを数多くを取るとサンプルの平均値は元の分布の平均値を中心とした正規分布で表現できる』
このままでは分かり難いので、日常的な例を使って説明しましょう。
お酒のつまみにナッツの盛り合わせがありますが、いろいろな種類が混じっていますね。ピーナッツのような小さなものから、アーモンドやカシューナッツのような大きなものまで、重さにばらつきがあります。
さて、ここにこのようなナッツが詰まった大きな袋(米俵一俵分)があるとします。このナッツの重さ分布表を作成することにしましょう。ピーナッツ1粒はだいたい2グラムぐらいです。アーモンドやカシュナッツはもう少し重く、4グラムから7グラムぐらいあります。袋からナッツを一つづつ取り出して重さを測定して下さい。それらを0.5グラム単位で一つのビン(組)として数えます。

図1:袋一杯分のナッツの重さ分布
このように袋一杯のナッツの重さ分布はとても正規分布とはいえませんね。当然ですよね!もともといろいろな種類のナッツが混じっていたのですから。つまり一般的に分布といった場合には必ずしも 一種類だけを対象とした分布を言っているのではないのです。 さて、測定が終わったナッツを全部元の袋に戻して下さい。 そして、今度は袋からナッツを5粒適当に取り出してまた一つづつ重さを測定して下さい。そして、その5粒の重さの平均値を計算します。
表1:5粒のナッツ重さの表

ナッツ5粒の平均値と袋全体の平均値(4.20)を比較してみて下さい。かなり異なっていますね。これはナッツが必ずしも均一に分布していないことから当然のことといえます。
このようにナッツを5粒とっては、1粒づつ重さを測定してその平均値を記録してみましょう。次図は最初の25回、50回、100回、1200回の場合の測定値を示します。
図2:5粒のナッツの重さの平均値の推移
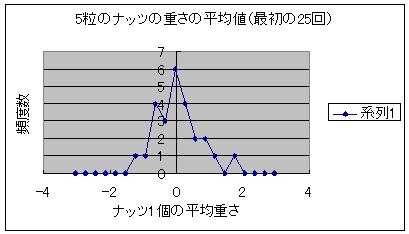
図2-1 最初の25回

図2-2 最初の50回
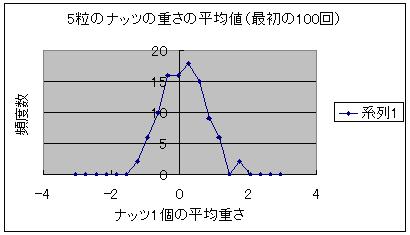
図2-3 最初の100回

図2-4 1200回
どうですか、ナッツ5粒の重さの平均値が袋全体の平均値(ゼロ点)を中心とした釣鐘状のグラフとなるのが分かるでしょう。この形が正規分布です。びっくりしましたか?この現象の意味する所を考えてみましょう。もともと袋から取り出した5粒のナッツは袋一杯のナッツの一部分であるので、もし、完全に均一に詰まっていたならナッツの重さ平均は袋全体の重さ平均と完全に一致するはずです。
このようにサンプルを取り出してその平均値を求める作業を繰り返していくと元の分布形状に全く無関係にサンプルの平均値の分布は全体の平均値(つまり一番頻度が大きい点)であるというのがこの中心極限定理の意味するところでした。
同じくこの図の一連の変化を見ると、サンプル数が増加するに従って、サンプルの平均値が本来の値に収斂していくのが分かります。大数の法則も同時に分かる例といえるでしょう。
続く...
さて、セイキは漢字では、精機、性器だけでなく、世紀、正規、生起、などいろいろあります。しかしこのエッセー『数財探掘』がテーマとしているデータ解析ではセイキといえば当然『正規』という漢字を思い浮かべるはずです。またこれはガウスが発見したので、ガウシアン分布(Gaussian Distribution)とも言われます。
皆さんも高校で確率分布の代表として、綺麗な釣鐘状の正規分布を習ったことがあるでしょう。数式的に言えば、指数関数なので扱いやすい関数です。またいろいろな式変形も華麗で、魅惑的な関数です。そのうち、なんとなく、分布といえば全てが正規分布であるのが当然であるような錯覚に陥ってしまう人が多いようです。
これはある程度正しい感覚でしょう。特に自然界の現象を測定してみると正規分布が至るところでみることが出来ます。例えば、ある特定のグループの人間の身長や体重などの分布はそうでしょう。正規分布は背後に自然界の物理的・生物的な法則が厳然として存在している場合にかなり多く見られるものです。
このように、正規分布が多く使われているために誤解が発生しています。この話をしましょう。大数の法則と中心極限定理(central limit theorem)は確率論ではよく使われる概念です。
まず大数の法則の意味するところは至って簡単です。つまり、『たくさんサンプルをとるとその平均値は本来の値に近づくと』ということです。例えば野球選手の打率を考えてみましょう。たとえイチロウのような選手でも一試合だけを見ると全く打てないときもあるわけですから、3割打者といえども6回の打席で必ずヒットを2回打てるとは限りません。しかし120打席以上であれば40回以上のヒットは必ず打てるのです。つまり、打席の回数が多くなれば、イチロウ本来の打率に相当するだけのヒットは出るわけです。これが大数の法則といわれるものです。
このような簡単なことでも法則となって数式などを使って説明されると、なんとなく難しく感じて本来的な意味が分からなくなってしまうようです。数学が苦手な人は数式に惑わされてその数式が意図するところを理解しようとせずにあきらめてしまうのが原因のように私には思えます。一度、数式を離れて、普通の言葉でそれがどのような意図、意味を持ったものなのかを考えてから、数式を眺めると、意味あいが納得できるでしょう。喩えていえば、カラオケでは日本語の歌は意味が分かるので、しっかり歌えますが、英語の歌はリズムはわかるものの文の意味が分からないので歌えないことが多いものです。しかし、ディスプレイで文が表示されるとつづりと意味が分かるので結構歌えるでしょう。数式の理解もこの要領です。自分の身近な世間的な例と比較しながら、考えると数式も比較的易しく理解できるものなのです。
もう一つの中心極限定理も統計データ処理によく使われる概念ですが世間ではよく誤解されてます。その誤解とは、『サンプルを数多くを取ると結局その分布は正規分布で表現できる』というものです。つまりサンプル数が少ないときは色々な分布を示していても、サンプル数を大きくすると本来の分布である正規分布に収束していく、と言うものです。
もしこれが正しいならば、正規分布一つがあれば全ての現象が表現できることになるはずですね。統計を学ばなくても、これはどこかおかしい!と感じるはずですが、統計を学んだはずの人の中にも、これを堂々と主張する人がいるのは驚きを通り越して、あきれます。統計というと数式がいくつも出てきて難しそうに見えますがたいていは一般常識で考えられる範囲の事を数式化したに過ぎないものだと私は思っています。
それでは、中心極限定理は正しくはどう解釈すべきでしょうか?その鍵は『平均値』という語句にあります。つまり中心極限定理とは正しくは次のように次のような意味です。『サンプルを数多くを取るとサンプルの平均値は元の分布の平均値を中心とした正規分布で表現できる』
このままでは分かり難いので、日常的な例を使って説明しましょう。
お酒のつまみにナッツの盛り合わせがありますが、いろいろな種類が混じっていますね。ピーナッツのような小さなものから、アーモンドやカシューナッツのような大きなものまで、重さにばらつきがあります。
さて、ここにこのようなナッツが詰まった大きな袋(米俵一俵分)があるとします。このナッツの重さ分布表を作成することにしましょう。ピーナッツ1粒はだいたい2グラムぐらいです。アーモンドやカシュナッツはもう少し重く、4グラムから7グラムぐらいあります。袋からナッツを一つづつ取り出して重さを測定して下さい。それらを0.5グラム単位で一つのビン(組)として数えます。

図1:袋一杯分のナッツの重さ分布
このように袋一杯のナッツの重さ分布はとても正規分布とはいえませんね。当然ですよね!もともといろいろな種類のナッツが混じっていたのですから。つまり一般的に分布といった場合には必ずしも 一種類だけを対象とした分布を言っているのではないのです。 さて、測定が終わったナッツを全部元の袋に戻して下さい。 そして、今度は袋からナッツを5粒適当に取り出してまた一つづつ重さを測定して下さい。そして、その5粒の重さの平均値を計算します。
表1:5粒のナッツ重さの表

ナッツ5粒の平均値と袋全体の平均値(4.20)を比較してみて下さい。かなり異なっていますね。これはナッツが必ずしも均一に分布していないことから当然のことといえます。
このようにナッツを5粒とっては、1粒づつ重さを測定してその平均値を記録してみましょう。次図は最初の25回、50回、100回、1200回の場合の測定値を示します。
図2:5粒のナッツの重さの平均値の推移

図2-1 最初の25回

図2-2 最初の50回

図2-3 最初の100回

図2-4 1200回
どうですか、ナッツ5粒の重さの平均値が袋全体の平均値(ゼロ点)を中心とした釣鐘状のグラフとなるのが分かるでしょう。この形が正規分布です。びっくりしましたか?この現象の意味する所を考えてみましょう。もともと袋から取り出した5粒のナッツは袋一杯のナッツの一部分であるので、もし、完全に均一に詰まっていたならナッツの重さ平均は袋全体の重さ平均と完全に一致するはずです。
このようにサンプルを取り出してその平均値を求める作業を繰り返していくと元の分布形状に全く無関係にサンプルの平均値の分布は全体の平均値(つまり一番頻度が大きい点)であるというのがこの中心極限定理の意味するところでした。
同じくこの図の一連の変化を見ると、サンプル数が増加するに従って、サンプルの平均値が本来の値に収斂していくのが分かります。大数の法則も同時に分かる例といえるでしょう。
続く...
















