最近ある会社で、ログ分析の仕方を議論していました。皆さんもご存知かと思いますが、ログ分析とは、あるWebサイトにアクセスしたユーザーがある画面から別の画面に遷移する時間、あるいはそのサイトに滞留している時間(いわゆる利用時間)の傾向を調査するものです。
大抵のサイトでのアクセスログは膨大な件数になりますこういう大量データはどのように情報に集約、すなわち指標化、するのが良いのでしょうか?
一番なじみ深いのは平均値でしょう。しかしその平均値にもいくつかの種類があります。普通言われているのは、単純平均、あるいは算術平均と呼ばれるもので、合計をそのサンプル数で割るものです。

しかし、これ以外にも幾何平均と調和平均と言われる平均値があります。
幾何平均は物価や賃金などの上昇率の平均値を求めるときに使います。
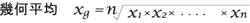
例えば、過去3年間の上昇率が、それぞれ、20%, 15%, 10% だった場合の平均上昇率は単純平均(算術平均)では15%となりますがこれは正しくはありません。正しくは幾何平均を取り、14.42%です。
もうひとつの平均値は調和平均と呼ばれるものです。それは、例えば自動車の速度の平均値を求めるときなどに使います。

ドライブに行った時、行きの平均時速が60Km、帰りの平均時速が80Kmの時の平均時速は、単純平均(算術平均)では70Kmですが、これは正しくありません。正しくは調和平均をとり、68.57Kmです。
このように平均値一つとってもいろいろな種類があるのです。
これ以外にも、代表値にはメディアンという値もあります。メディアンというのは小学校などで背の順に子供を並べるように、データの値を小さいものから順に並べ、その真ん中の値をとります。例えば、6つのデータがあり、その値が: 1, 1.3, 1.5, 2.2, 2.8, 6とすると、単純平均では2.47ですが、メディアンはデータの3番目の値と4番目の値の半分である 1.85 となります。
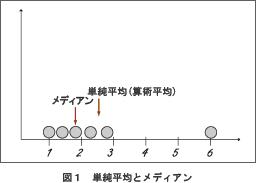
メディアンには外れ値に強いという特徴があります。この場合、最後の6という値が一つだけ他の値と大きく外れていますね。これは正しい値であるかもしれませんが、例外的な値、あるいは測定誤差とも考えられます。このようなとき、例外値の影響を受けにくい手法を採用する必要があります。それには、単純平均よりメディアンの方が適切です。なぜなら、単純平均では、外れ値そのものが大きく効いてきて、平均値が本来の数値より大きく(あるいは逆に小さく)なりますが、メディアンの場合は、外れ値を持っているデータサンプルの個数しか効いてきませんので、大抵はデータが固まっている(即ち、大多数の)データサンプル点に近い値となります。
さて、データの代表値として(算術)平均値だけで良いでしょうか?
次の例を考えてみましょう。あなたが、株を買うとします。2つの銘柄の過去1年の平均値は一株あたりどちらも5万円だったとします。しかし、一つの銘柄は変動がほとんどなく、安定的に5万円であるとします。もう一つの銘柄は値の上下が激しく、最低2万円のときもあれば、最高8万円のときもある、いわゆるジェットコースターのような変動をする株です。さて、あなたはどちらを買いますか?冒険を好むタイプの人は後の方の株を買うでしょう。それは損をすることがあっても、ぼろ儲けすることもあるからです。一方、絶対に損をしたくない、という保守的な人はどう考えるでしょうか?安定的な前者の株を買うのではないでしょうか。
この例でも分かるように、平均値が同じでも、変動値(Variance)が異なると、状況が異なるのです。つまり、人間の判断は単純な平均値だけでは決まらないのです。
この点を別の例を使ってもう少し詳しく説明しましょう。
皆さんも終電を乗り継いで家に帰る時に乗り継ぎが悪くて、あるいは乗り過ごして、タクシーで高い金を払う破目になった経験があるでしょう。

つまりX駅で終電Aを乗り、Y駅で終電Bに乗り換えます。このとき、終電Aが時刻通りに着くと、乗り換えに1分の余裕があります。
終電Aに乗りそこなうと、X駅から家までタクシーで帰らないといけません。X駅から家までのタクシー代は3万円かかるとします。Y駅で終電Bに乗りそこなうと、そこからタクシーで帰らないといけません 。Y駅から家までのタクシー代は1万円とします。
このとき、最初の終電AがX駅を出発するタイミングは遅かったり早かったりですが、終電Bは時刻表通り正確に発車するとします。
このような状況で、終電AがX駅を発車するパターンが次のように4つあったとしましょう。いづれのパターンも発車時刻の平均値はゼロで同じです。

問題は、これらのそれぞれ4つのパターンの時あなたは、次の問い
にどう答えますか?


どうですか?平均値が同じでも、ばらつき(Variance)の値によって、行動がずいぶん変わってきますね!つまり、平均値は事実の一面しか表現できないので、行動を決定するには情報として不十分なのです。実際金融業界で使われているデリバティブは資産価値の変動分(Volatility)、つまりばらつきを重要なファクターとして計算式に取り入れているのです。
続く...
大抵のサイトでのアクセスログは膨大な件数になりますこういう大量データはどのように情報に集約、すなわち指標化、するのが良いのでしょうか?
一番なじみ深いのは平均値でしょう。しかしその平均値にもいくつかの種類があります。普通言われているのは、単純平均、あるいは算術平均と呼ばれるもので、合計をそのサンプル数で割るものです。

しかし、これ以外にも幾何平均と調和平均と言われる平均値があります。
幾何平均は物価や賃金などの上昇率の平均値を求めるときに使います。
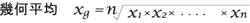
例えば、過去3年間の上昇率が、それぞれ、20%, 15%, 10% だった場合の平均上昇率は単純平均(算術平均)では15%となりますがこれは正しくはありません。正しくは幾何平均を取り、14.42%です。
もうひとつの平均値は調和平均と呼ばれるものです。それは、例えば自動車の速度の平均値を求めるときなどに使います。

ドライブに行った時、行きの平均時速が60Km、帰りの平均時速が80Kmの時の平均時速は、単純平均(算術平均)では70Kmですが、これは正しくありません。正しくは調和平均をとり、68.57Kmです。
このように平均値一つとってもいろいろな種類があるのです。
これ以外にも、代表値にはメディアンという値もあります。メディアンというのは小学校などで背の順に子供を並べるように、データの値を小さいものから順に並べ、その真ん中の値をとります。例えば、6つのデータがあり、その値が: 1, 1.3, 1.5, 2.2, 2.8, 6とすると、単純平均では2.47ですが、メディアンはデータの3番目の値と4番目の値の半分である 1.85 となります。

メディアンには外れ値に強いという特徴があります。この場合、最後の6という値が一つだけ他の値と大きく外れていますね。これは正しい値であるかもしれませんが、例外的な値、あるいは測定誤差とも考えられます。このようなとき、例外値の影響を受けにくい手法を採用する必要があります。それには、単純平均よりメディアンの方が適切です。なぜなら、単純平均では、外れ値そのものが大きく効いてきて、平均値が本来の数値より大きく(あるいは逆に小さく)なりますが、メディアンの場合は、外れ値を持っているデータサンプルの個数しか効いてきませんので、大抵はデータが固まっている(即ち、大多数の)データサンプル点に近い値となります。
さて、データの代表値として(算術)平均値だけで良いでしょうか?
次の例を考えてみましょう。あなたが、株を買うとします。2つの銘柄の過去1年の平均値は一株あたりどちらも5万円だったとします。しかし、一つの銘柄は変動がほとんどなく、安定的に5万円であるとします。もう一つの銘柄は値の上下が激しく、最低2万円のときもあれば、最高8万円のときもある、いわゆるジェットコースターのような変動をする株です。さて、あなたはどちらを買いますか?冒険を好むタイプの人は後の方の株を買うでしょう。それは損をすることがあっても、ぼろ儲けすることもあるからです。一方、絶対に損をしたくない、という保守的な人はどう考えるでしょうか?安定的な前者の株を買うのではないでしょうか。
この例でも分かるように、平均値が同じでも、変動値(Variance)が異なると、状況が異なるのです。つまり、人間の判断は単純な平均値だけでは決まらないのです。
この点を別の例を使ってもう少し詳しく説明しましょう。
皆さんも終電を乗り継いで家に帰る時に乗り継ぎが悪くて、あるいは乗り過ごして、タクシーで高い金を払う破目になった経験があるでしょう。

つまりX駅で終電Aを乗り、Y駅で終電Bに乗り換えます。このとき、終電Aが時刻通りに着くと、乗り換えに1分の余裕があります。
終電Aに乗りそこなうと、X駅から家までタクシーで帰らないといけません。X駅から家までのタクシー代は3万円かかるとします。Y駅で終電Bに乗りそこなうと、そこからタクシーで帰らないといけません 。Y駅から家までのタクシー代は1万円とします。
このとき、最初の終電AがX駅を出発するタイミングは遅かったり早かったりですが、終電Bは時刻表通り正確に発車するとします。
このような状況で、終電AがX駅を発車するパターンが次のように4つあったとしましょう。いづれのパターンも発車時刻の平均値はゼロで同じです。

問題は、これらのそれぞれ4つのパターンの時あなたは、次の問い
にどう答えますか?


どうですか?平均値が同じでも、ばらつき(Variance)の値によって、行動がずいぶん変わってきますね!つまり、平均値は事実の一面しか表現できないので、行動を決定するには情報として不十分なのです。実際金融業界で使われているデリバティブは資産価値の変動分(Volatility)、つまりばらつきを重要なファクターとして計算式に取り入れているのです。
続く...
















