nanaponさんより「複雑系」を取り上げていました。
===== nanaponさんのコメント =====
>本当に複雑系について知りたいのかな?
と言われると困りますが、猿でもわかるくらいには興味あります。
と言うことで、複雑系のイメージについて書きたいと思います。
<学問から社会へ>
数学の研究⇒物理学の応用⇒社会での活用 という順番で学問から社会への応用となります。
例えで言えば、携帯電話を想像して見てください。
通信でやり取りをしているのは、電波ではないでしょうか?
数学の研究では、三角形より三角関数を研究しました。 ※高校で習う、sin、cos、tanですね!
物理学の応用では、波(電波など)を応用して研究しました。
社会では、携帯のやり取りに電波を利用しました。
数学の研究(三角関数)⇒物理学の応用(波)⇒社会(携帯電話の電波)
数学の研究⇒物理学の応用⇒社会での活用という流れを頭に置いて欲しいと思います。
<複雑系>
複雑系の場合は、数学の研究⇒社会での活用となり物理の応用がありません。
※もちろん、物理で研究している方はいます。
数学の研究(カオス・フラクタル)
社会では、複雑な経済(複雑系経済学)
という風に複雑系を扱います。
私が言っているのでは、数学の研究のカオス・フラクタルのことです。
nanaponさんが言っているのが、社会での複雑系経済学のことだと思います。
つまり、私は複雑系の出発点を言っています。 nanaponさんは、複雑系の応用についての記事を書かれているのですね!
<カオスとフラクタル>
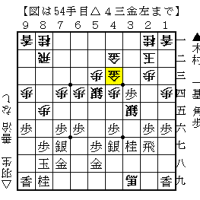
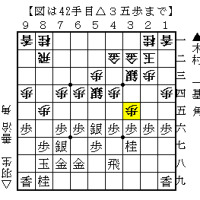
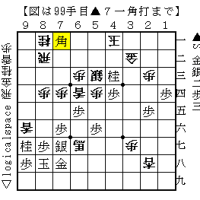
カオスとフラクタルを将棋の例を見て説明しましょう!
(図A)
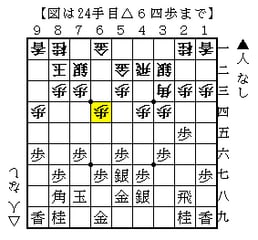
(図B)

図Aと図Bは、△6四歩と△5四歩の違いだけです。
図Aは△6四歩なので、▲3五歩からの仕掛けが成立します。
図Bは△5四歩なので、▲3五歩からの仕掛けが無理筋です。 △6四角があるためですね!
図Bでは、▲4五歩早仕掛け、棒銀戦法が有力であります。
※図Aと図Bの違いが分かるのは、アマ二段以上と言われていましたけど。
ざっくりに言います。
カオスとは、初期値によって、結果が変わることです。
フラクタルとは、図形の配置(繰り返し処理を含む)です。
将棋では言えば、図Aと図Bでは▲3五歩の仕掛けが成立するのかどうかの結果が、カオスと言えます。
図Aと図Bの駒の配置をフラクタルと考えれば良いと思います。
※カオスとフラクタルを将棋に例えるのは、あまりにも極端だと思いますけど、将棋のブログなので、分かりやすさを重要視しました。
<画像の数式>
カオスとフラクタルの図形より
カオスの例です。
離散系のカオス(1)の「2.翼のようなストレンジアトラクタ」を見て下さい。
3つの画像がありますね!
xn + 1 = axn + byn + c + d/(1+xn2) ・・・①
yn + 1 = -xn ・・・②
3つの画像は、①、②の数列を描いた物なのです。 ※数列は高校で習います。
左の画像:a=-0.9,b=0.96,c=-4.0,d=5.0, x0=1.0,y0=0.0
中の画像:a=-1.57,b=0.96,c=-4.0,d=5.0, x0=1.0,y0=0.0
右の画像:a=-1.76,b=0.96,c=-4.0,d=5.0, x0=1.0,y0=0.0
3つの画像は、aの値が異なるだけで、他は同じです。
しかし、画像として見ると、全く違う数列の画像に見えます。
同じことを書きますが、カオスとは、初期値によって、結果が変わることです。
つまり、aの値によって、画像が違うので、これがカオスであります。
※aの値が初期値、画像が結果です。
フラクタルの例です。
マンデルブロ集合の「1.f(z)=z2+c」を見てください。
4つの図がありますね!
f(z)=z2+c・・・③
4つの画像は、③の複素数列を描いた物なのです。 ※複素数列は理系の大学2年生で習います。
左から順番に、X1、X2、X3、X4と名前を付けます。
X1:z0=0, c=a+bi, a:-1.485~-1.473, b:-0.006~0.006
X2:z0=0, c=a+bi, a:-1.266~-1.246, b:0.371~0.391
X3:z0=x0+y0i, c=-0.035+0.795i, x0:-1.4~1.4,y0:-1.4~1.4
X4:z0=x0+y0i, c=-0.704+0.28i, x0:-0.27~0.13,y0:0.51~0.91
4つの画像は、同じ複素数列を見ていますが、見る範囲によって見え方が異なるということです。
同じことを書きますが、フラクタルとは、図形の配置(繰り返し処理を含む)です。
※図形の配置が複素数列となります。
※繰り返し処理の事を、数学の用語では自己相似性と言います。
===== 数学的な自己相似形について =====
③の式は、zn + 1 = zn + cが正確な表現です。
fn + 1(z) = fn(z) と f を n 回繰り返していますね!
この f を n 回繰り返していることが、自己相似性と言います。
もちろん、n → ∞ とすれば、限りなく表現できることは分かると思います。
===== ここまで =====
ただし、フラクタルは、次のことが必要十分条件です。 つまり、フラクタルの定義です。
<フラクタルの定義>
集合Kの位相次元 dimT(K) とハウスドルフ次元 dimH(K)について、
dimT(K) < dimH(K)
が成立するとき、集合Kはフラクタルであるという。
※位相、ハウスドルフ、次元とかは、数学用語なので、理系の方を除いて理解する必要がありません。
数学的には、フラクタルの定義は必要でありますが、複雑系を考える時には、フラクタルの定義に重きを置く必要はありません。
<複雑系経済学>
カオスとフラクタルからは、何を学んだのでしょうか?
・初期状態によって、結果が異なる(カオス)
・同じ物でも範囲が異なれば見方が異なる(フラクタル)
複雑系経済学では、一般に非線形で、要素間の相互依存性が強い系は複雑系となる可能性がある。
特に経済学にとっては要素の数が多いことや収穫逓増現象が重要である。
要素間の相互依存性が強い系とは、複数の初期状態と異なる結果には、因果関係があるということですね!
この相互依存性を因果関係と言っているので、何だか難しいように聞こえますね!
私は、複雑系経済学は専門外なので、簡単にしか触れません。
nanaponさんの「田坂広志さんのメルマガから引用」して「複雑系」を取り上げています。
田坂広志さんは、経済を複雑系経済学の1側面として考えて取り上げていると思います。
===== LogicalInSpaceの感想 =====
単純化と複雑系のどちらが良いのか? 議論を呼ぶと思いますけど。 研究する範囲では、両方が必要であると思います。
社会では、どのようにアプローチするのかが重要なことであると思います。
世の中(自然界、経済)は、簡単な事より複雑な事の方が多い事も事実だと思います。
複雑系経済学は、まだまだ進化する学問だと思いますし、実経済もどんどん変化すると思います。
前回の記事をもう1度、読んでみてください。 少しイメージが出来ると思いますよ!
===== nanaponさんのコメント =====
>本当に複雑系について知りたいのかな?
と言われると困りますが、猿でもわかるくらいには興味あります。
と言うことで、複雑系のイメージについて書きたいと思います。
<学問から社会へ>
数学の研究⇒物理学の応用⇒社会での活用 という順番で学問から社会への応用となります。
例えで言えば、携帯電話を想像して見てください。
通信でやり取りをしているのは、電波ではないでしょうか?
数学の研究では、三角形より三角関数を研究しました。 ※高校で習う、sin、cos、tanですね!
物理学の応用では、波(電波など)を応用して研究しました。
社会では、携帯のやり取りに電波を利用しました。
数学の研究(三角関数)⇒物理学の応用(波)⇒社会(携帯電話の電波)
数学の研究⇒物理学の応用⇒社会での活用という流れを頭に置いて欲しいと思います。
<複雑系>
複雑系の場合は、数学の研究⇒社会での活用となり物理の応用がありません。
※もちろん、物理で研究している方はいます。
数学の研究(カオス・フラクタル)
社会では、複雑な経済(複雑系経済学)
という風に複雑系を扱います。
私が言っているのでは、数学の研究のカオス・フラクタルのことです。
nanaponさんが言っているのが、社会での複雑系経済学のことだと思います。
つまり、私は複雑系の出発点を言っています。 nanaponさんは、複雑系の応用についての記事を書かれているのですね!
<カオスとフラクタル>
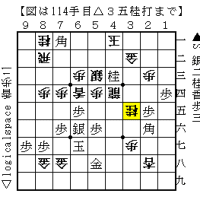
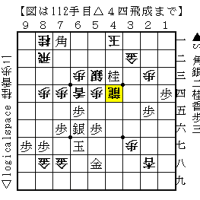
カオスとフラクタルを将棋の例を見て説明しましょう!
(図A)

(図B)

図Aと図Bは、△6四歩と△5四歩の違いだけです。
図Aは△6四歩なので、▲3五歩からの仕掛けが成立します。
図Bは△5四歩なので、▲3五歩からの仕掛けが無理筋です。 △6四角があるためですね!
図Bでは、▲4五歩早仕掛け、棒銀戦法が有力であります。
※図Aと図Bの違いが分かるのは、アマ二段以上と言われていましたけど。
ざっくりに言います。
カオスとは、初期値によって、結果が変わることです。
フラクタルとは、図形の配置(繰り返し処理を含む)です。
将棋では言えば、図Aと図Bでは▲3五歩の仕掛けが成立するのかどうかの結果が、カオスと言えます。
図Aと図Bの駒の配置をフラクタルと考えれば良いと思います。
※カオスとフラクタルを将棋に例えるのは、あまりにも極端だと思いますけど、将棋のブログなので、分かりやすさを重要視しました。
<画像の数式>
カオスとフラクタルの図形より
カオスの例です。
離散系のカオス(1)の「2.翼のようなストレンジアトラクタ」を見て下さい。
3つの画像がありますね!
xn + 1 = axn + byn + c + d/(1+xn2) ・・・①
yn + 1 = -xn ・・・②
3つの画像は、①、②の数列を描いた物なのです。 ※数列は高校で習います。
左の画像:a=-0.9,b=0.96,c=-4.0,d=5.0, x0=1.0,y0=0.0
中の画像:a=-1.57,b=0.96,c=-4.0,d=5.0, x0=1.0,y0=0.0
右の画像:a=-1.76,b=0.96,c=-4.0,d=5.0, x0=1.0,y0=0.0
3つの画像は、aの値が異なるだけで、他は同じです。
しかし、画像として見ると、全く違う数列の画像に見えます。
同じことを書きますが、カオスとは、初期値によって、結果が変わることです。
つまり、aの値によって、画像が違うので、これがカオスであります。
※aの値が初期値、画像が結果です。
フラクタルの例です。
マンデルブロ集合の「1.f(z)=z2+c」を見てください。
4つの図がありますね!
f(z)=z2+c・・・③
4つの画像は、③の複素数列を描いた物なのです。 ※複素数列は理系の大学2年生で習います。
左から順番に、X1、X2、X3、X4と名前を付けます。
X1:z0=0, c=a+bi, a:-1.485~-1.473, b:-0.006~0.006
X2:z0=0, c=a+bi, a:-1.266~-1.246, b:0.371~0.391
X3:z0=x0+y0i, c=-0.035+0.795i, x0:-1.4~1.4,y0:-1.4~1.4
X4:z0=x0+y0i, c=-0.704+0.28i, x0:-0.27~0.13,y0:0.51~0.91
4つの画像は、同じ複素数列を見ていますが、見る範囲によって見え方が異なるということです。
同じことを書きますが、フラクタルとは、図形の配置(繰り返し処理を含む)です。
※図形の配置が複素数列となります。
※繰り返し処理の事を、数学の用語では自己相似性と言います。
===== 数学的な自己相似形について =====
③の式は、zn + 1 = zn + cが正確な表現です。
fn + 1(z) = fn(z) と f を n 回繰り返していますね!
この f を n 回繰り返していることが、自己相似性と言います。
もちろん、n → ∞ とすれば、限りなく表現できることは分かると思います。
===== ここまで =====
ただし、フラクタルは、次のことが必要十分条件です。 つまり、フラクタルの定義です。
<フラクタルの定義>
集合Kの位相次元 dimT(K) とハウスドルフ次元 dimH(K)について、
dimT(K) < dimH(K)
が成立するとき、集合Kはフラクタルであるという。
※位相、ハウスドルフ、次元とかは、数学用語なので、理系の方を除いて理解する必要がありません。
数学的には、フラクタルの定義は必要でありますが、複雑系を考える時には、フラクタルの定義に重きを置く必要はありません。
<複雑系経済学>
カオスとフラクタルからは、何を学んだのでしょうか?
・初期状態によって、結果が異なる(カオス)
・同じ物でも範囲が異なれば見方が異なる(フラクタル)
複雑系経済学では、一般に非線形で、要素間の相互依存性が強い系は複雑系となる可能性がある。
特に経済学にとっては要素の数が多いことや収穫逓増現象が重要である。
要素間の相互依存性が強い系とは、複数の初期状態と異なる結果には、因果関係があるということですね!
この相互依存性を因果関係と言っているので、何だか難しいように聞こえますね!
私は、複雑系経済学は専門外なので、簡単にしか触れません。
nanaponさんの「田坂広志さんのメルマガから引用」して「複雑系」を取り上げています。
田坂広志さんは、経済を複雑系経済学の1側面として考えて取り上げていると思います。
===== LogicalInSpaceの感想 =====
単純化と複雑系のどちらが良いのか? 議論を呼ぶと思いますけど。 研究する範囲では、両方が必要であると思います。
社会では、どのようにアプローチするのかが重要なことであると思います。
世の中(自然界、経済)は、簡単な事より複雑な事の方が多い事も事実だと思います。
複雑系経済学は、まだまだ進化する学問だと思いますし、実経済もどんどん変化すると思います。
前回の記事をもう1度、読んでみてください。 少しイメージが出来ると思いますよ!












※コメント投稿者のブログIDはブログ作成者のみに通知されます