
![]()
ブログ人気投票にクリックいただけると幸いです!
今春の中学入試に出題された、男女御三家の算数の問題を取り上げ、その傾向と対策について幾つか問題をピックアップして分析しています。今日は、下のブログに続いて雙葉中学校の解説二回目です。前回は、問題【4】を取り上げました。今日は、最後の問題【5】について、解説しましょう。
マッキーの学習指導法:今年の雙葉中学校入試問題「算数」・・・その1
【問題5】
あるバス停には、A駅行きのバスとB駅行きのバスが来ます。A駅行きは午前7時11分から17分間隔で来ます。B駅行きは午前6時35分から4分、7分、4分、7分、・・・・の間隔で来ます。バスの停車時間は考えません。
(1)このバス停に午前11時以降で最初に来るバスは、午前11時何分の何駅行きですか。
(2)このバス停に2種類のバスが初めて同時に来るのは、午前何時何分ですか。
(3) (2)を1回目とします。6回目にこのバス停に同時にバスが来るのは何時何分ですか。午前、午後も答えましょう。
【解説・解答】
バス停に等間隔で到着する複数の行き先のバス時刻に関する問題です。等差数列・公倍数などの理解を問う問題で、一般的な問題と言えるでしょう。
ただし、この問題は、一方のバスが4分、7分、4分、7分という周期的な間隔で運行している点が、考慮できるかどうかがポイントとなります。4分と7分の和の11分周期としてまずは考えるべきでしょう。
(1)の問題です。A駅行きは、午前7時11分から17分間隔ですので、A駅行きバスで11時過ぎに最初に到着する時刻を計算します。
(11-7と11/60)÷17/60=13と8/17
よって、7時11分+17分×14=11時9分
同様に、B駅行きは午前6時35分から11分間隔周期としてまずは計算します。
(11-6と35/60)÷11/60=24と1/11
よって、6時35分+11分×25=11時10分
4分、7分の周期を考慮して、ひとつ前のバスは、11時10分-7分=11時3分
よって、午前11時3分のB駅行きバスが正解です。
(2)A駅行き・・・午前7時11分から17分間隔、B駅行き・・・午前6時35分から4分・7分周期の間隔という変則的な条件を考えます。
A駅行きのバスとB駅行きの周期の最初の4分のバスとが初めて同時に到着する時刻・・・(ⅰ)と、A駅行きのバスとB駅行きの周期の後の7分のバスとが初めて同時に到着する時刻・・・(ⅱ)の両方を書き並べて調べますが、そんなに時間はかかりません。
(ⅰ)は、7時45分に最初に同時に到着します。
(ⅱ)は、8時36分に最初に同時に到着することが分かります。
よって、このことから求める答えは、7時45分となります。
(3)は、(2)で求めた7時45分を1回目として、6回目にこのバス停に同時にバスが来る時刻を求める問題です。(2]ができていれば、そんなに難しい問題ではありません。
(2)の(ⅰ)のB駅行きバスとA駅行きバスは、7時45分から17と11の最小公倍数の187分を公差とする等差数列の時刻で同時に到着します。・・・この手の問題は一般的な問題!
また、(ⅱ)のB駅行きバスとA駅行きバスは、8時36分から187分間隔で同時に到着します。
この条件から、6回目に同時にバスが来る時刻を求めます。
(ⅰ)のB駅行きバスとA駅行きバス・・・7時45分、10時52分、13時59分・・・
(ⅱ)のB駅行きバスとA駅行きバス・・・8時36分、11時43分、14時50分・・・
以上の結果から、14時50分=午後2時50分が求める答えとなります。
公倍数・最小公倍数と、規則的な周期を考える問題です。「数の性質」を使う問題は、改訂された高校数学Aに「整数の性質」として加えられたことでも分かるように、重要な学習課題です。減少傾向にあった数の性質の問題は、中学入試においても近年出題の割合が増加している分野です。しっかりと学習しておきましょう。

![]()
ブログ人気投票にクリックいただけると幸いです!
今年度の中学入試で出題された算数の問題について、問題傾向と対策を学校別に綴っています。今日は、女子御三家の三番手として雙葉中学の算数を取り上げます。
今年の雙葉中学算数問題は、問題【1】が小問4題構成で、計算1題・割合の問題1題、旅人算1題、混合算1題の出題となっています。いずれも基本的な問題です。
問題【2】は、仕切りのある水槽に、水を入れる管と、水が出ていく栓が取り付けられている設定で、この問題も一般的な問題と言えます。ただし、この容積に関する問題は、様々に条件を変形することができ、グラフを絡めた問題としても出題されます。
問題【3】は、黒と白の碁石を正六角形に交互に並べていく問題です。規則性を見つけると、等差数列になっていることに気付くはずです。(2)と(3)はそのことを前提として、問題を発展させた出題となっています。
問題【4】は、今回解説する問題です。図の中の斜線を付けた部分の面積を求めるのですが、ちょっとした基本事項・・・このブログでも繰り返し指摘している事項を、しっかりと理解していれば、比較的簡単な問題と言えるでしょう。
問題【5】は、次の回に取り上げる問題です。2種類のバスの発車時刻の問題で、最小公倍数・公倍数を用いる一般的な問題です。しかし、一方のバスの発車時刻が、等差数列ではなく、4分・7分という間隔をくり返すことにより、だいぶ難しく感じられる問題に変化させています。注意深く条件を整理し、しっかりと書き上げて求める必要があります。こうした問題は、御三家らしい問題と言えるでしょう。
【問題】
下の図は、正方形と直角二等辺三角形と円を組み合わせたものです。
かげをつけた部分の面積は何平方cmですか。円周率は3.14です。
【解説・解答】
一辺が20cmの正方形を、等しい辺の長さが5cmの直角二等辺三角形と、一辺が5cmの正方形、それに中心に位置する円の三つの図形に注目して解きます。
かげをつけた部分の面積を求めるために、直角二等辺三角形の数を数えると12個。正方形の数は5個。しかしよく見ると、円から内接する正方形を除いた4つの弓型の面積を、それらの合計から引く必要があります。
さて、中心にある円の半径は出ていません。半径の長さは、実際には「2分の5ルート2cm」となります。公立中学校3年生で出てくる「三平方の定理」を学習するまで、この数値は出すことができません。ただ、かつて私の教室に通っていた小学4年生が、こうしたルートの入った数値を出すことができました。「中学3年生の数学まで学習したの?」・・・「いいえ、高校2年生まで学習しました。」
この生徒は、その後開成に合格しましたが、こうした特別な力を持つ生徒と同様の学力を要求している問題ではありません。
「半径が出ていなかったら、半径×半径の数値が出せないかを考える。」
この考えは、実は基本的なことです。円に内接する正方形の面積は、「一辺×一辺」で求めることができますが、正方形はおうぎ形の仲間ですので、「対角線×対角線÷2」でも求めることができます。
このことから、対角線=直径=半径×2ですので、
円に内接する正方形の面積は、(半径×2)×(半径×2)÷2=半径×半径×2=5×5、となることが分かります。
よって、半径×半径=12.5という数値が出てきます。
よって求める面積は、
5×5÷2×12+5×5×5-(12.5×3。14-5×5)
=150+125-14.25
=260.75平方センチメートル
今回の問題のように、問題の解法パターンを覚えておく事が必要な問題があります。以前に、そうした問題を昨年度の入試問題から集めて、「マッキーの一問必答」というタイトルで、(1)回から(13)回に分けて綴りました。興味ある方は、ネットで検索して御覧ください。

![]()
ブログ人気投票にクリックいただけると幸いです!
今春の中学入試に出題された、男女御三家の算数の問題を取り上げ、その傾向と対策について幾つか問題をピックアップして、問題傾向を分析しています。今日は、下のブログに続いて女子学院算数の解説二回目です。
マッキーの学習指導法:今年の女子学院中学校入試問題「算数」・・・その1
今日取り上げる問題は、最後の問題6です。通学時間に関する平均の問題で、時間の範囲を含む与えられた条件が理解できるかどうかがポイントとなります。
【問題6】
あるクラス30人の生徒の通学時間を調べたら、次のことが分かりました。
50分以上の生徒の通学時間の平均は、58分
50分未満の生徒の通学時間の平均は、24分
60分以上の生徒の通学時間の平均は、65分
60分未満の生徒の通学時間の平均は、27分
50分以上60分未満の生徒の人数は、5人
通学時間が60分以上の生徒の人数は□人で、クラス全体の通学時間の平均は□分□秒です。
【解説】
様々な解き方が考えられますが、通学時間が60分以上の生徒人数を□人として、文字式で条件を整理し、その式を解くことにより求めるのが、最も簡単な方法です。上位校を受験する場合、文字式で条件を整理する力が求められます。
通学時間が60分以上の生徒の人数を□人として、クラス30人の通学時間の合計を求めてみます。
60分以上の生徒と60分未満の生徒の通学時間の平均を用いると、
65×□+27×(30-□)
50分以上の生徒と50分未満の生徒の通学時間の平均を用いると、
58×(□+5)+24×(25-□)
無論のこと、二つの式は等しくなりますので、
65×□+27×(30-□)=58×(□+5)+24×(25-□)
左辺と右辺を整理すると、
38×□+810=34×□+890
4×□=80
□=20(人)・・・60分以上の生徒数
クラス全体の通学時間の合計は、上の式に代入して、38×20+810=1570
よって求めるクラス全体の通学時間の平均は、1570÷30=52と1/3(分)
52と1/3(分)=52分20秒・・・クラス全体の通学時間の平均
平均の問題は、総和(合計)を求めて計算する問題が基本形で、応用問題として面積図を用いて条件を整理する問題などが一般的です。今回の問題は、数値の範囲を絡めた問題で、文字式で解くと比較的簡単に解くことができます。
【追記】
ある方から、「この問題を満たす解が無い」のではないかという指摘がありました。今回問題を解いた数値を用いて、問題の確かめをしてみると、明らかにこの問題は、出題ミスだったことが分かりました。
では、皆さんが分かるように確かめをしてみましょう。
「60分以上の生徒の通学時間の平均は、65分」という条件から、その20人の総和は、65×20=1300(分)
「50分以上の生徒の通学時間の平均は、58分」という条件から、50分以上60分未満の生徒の人数5人を加えた25人の総和は、58×25=1450(分)
この結果から、50分以上60分未満の生徒の人数5人の総和は、1450-1300=150〈分)
よって、この5人の平均通学時間は、150÷5=30(分)となります。
通学時間50分以上60分未満の生徒5人の平均時間が、30分となってしまいますので、この問題の条件を満たす解は無いということになります。与えられた条件を鵜呑みに問題を解くと、私が出した答えが出てきます。しかし、設定された条件が、実は矛盾する設定だったという出題ミスでした。
入試を実施する前に訂正を出したのか、事後に配点考慮したのかは、情報はありません。明らかに恥ずかしい出題ミスも、毎年見かけます。今回の問題の出題者は、構成した問題を注意深くチェックして見るべきでした。私自身も、同様の表面的な解答をしただけでした。訂正して、お詫びします。

![]()
ブログ人気投票にクリックいただけると幸いです!
2月から3月にかけて、今春の中学入試に出題された、開成と桜蔭の算数の問題を取り上げ、その傾向と対策について綴りました。今度は、女子御三家の残り、女子学院・雙葉中学校の算数について、幾つか問題をピックアップして、数回に分けて問題傾向を分析します。
まず、今日は女子学院の算数を取り上げます。今年の女子学院の算数は、問題1で計算を含む6題で構成された小問が出題されています。(1)の計算は少々複雑な□の問題です。次の(2)は、演算記号を用いた整数の性質に関する問題。(3)は速さに関する基本的な問題、(4)が図形の角度、(5)が図形の周囲の長さを求める問題、そして(6)が正六角形に含まれる4つの三角形の面積を求める問題です。いずれの問題も、基本的な問題ですので、ミス無く素早く解く必要があります。
問題2は、つながれた犬が動くことができる範囲の面積を求める問題で、どちらかと言えば陳腐な問題です。
問題3は、機械の仕事率に関する問題で、今日はこの問題を取り上げます。
問題4は、容器を傾けて、こぼれる水の量と、元に戻した時の水面の高さを求める問題です。
問題5は、1週間を8日、1年を10ヶ月とする新たなカレンダーを作り、曜日と日付を考えさせる問題です。
最後の問題6は、通学時間と平均に関する問題で、時間の範囲を含む与えられた条件が理解できるかどうかがポイントとなります。最後の問題6は次の機会に取り上げます。
では、問題に入ります。
【問題3】 🔳にあてはまる数を入れ、【 】内はいずれかを◯で囲みなさい。
ある製品を1個作るのに、機械Aは0.6分、機械Bは1.2分、機械Cは1.3分かかります。この製品を2016個作るとき、Aだけで作る場合にかかる時間は🔳時間🔳分🔳秒で、BとCの2台で作る場合に比べて🔳分🔳秒だけ【長い、短い】です。
【解説】
機械の仕事率に関する問題です。Aだけで作る場合の時間の計算は、出されている数値の単位が1個あたりに費やす時間(分)で出されています。いわば、0.6分/個という数値です。したがって、所要時間を求めるためには、作る製品の個数にこの数値をかけて求めることができます。
0.6×2016=1209.6(分)・・・20時間9分36秒
では、BとCの2台で作る場合はどうでしょうか。この場合、仕事率を1個あたりを作る時間で考えるよりは、1分あたりに2つの機械で何個作ることができるかを計算した方が楽です。
Bは1分で、1÷1.2=5/6(個)作ることができます。また、Cは1分で、1÷1.3=10/13(個)作ることができます。したがって、BとCの2台で作る場合、1分で5/6+10/13=125/78(個)作ることができます。
このことから、BとCを用いてこの製品を2016個作るために要する時間は、個数を単位時間当たりの125/78(個)で割って求めることができます。
2016÷125/78=1257.984(分)
上の計算以外に、Bの1.2分と、Cの1.3分の最小公倍数15.6分で、二台の機械で計25個の製品を作ることができますので、これを使って計算することも可能です。15.6分を一周期として、何周期と幾つかの半端として計算します。子どもたちにこの問題を解かせた場合、この周期性を利用する考え方を使う生徒が多いかも知れません。
実はこの問題、ここからが勝負です。上の計算では、最後のところが、二つの機械が未完成品の合算で、2016個の製品ができた数値となっていることが理解できるでしょうか。ですから、ほんとうの完成時間は、この数値よりも多少長くなります。そこを微調整する必要がある問題です。計算で、正解の近くまで一気に持って行って、最後は微調整を行う問題は、上位校の問題で多く出題されます。
上で出した数値の整数部分1257分で、どのようになっているかをチェックしましょう。
1257分で、機械Bは1047個の製品を作り、0.6分余ります。機械Cは966個の製品を作り、1.2分余っています。よって、1257分では、二つの機械で製品を2013個作り、それどれちょっと時間を余しています。
最後の3個の製品が完成するのは、機械Cが1257分から1.4分後のこととなることが、調べると直ぐに分かるはずです。よって、機械BとCで製品2016個を完成させるための時間は、1258.4分後となります。
1258.4分=20時間58分24秒
20時間58分24秒-20時間9分36秒=48分48秒
よって、Aだけで作る場合にかかる時間は20時間9分36秒で、BとCの2台で作る場合に比べて「48分48秒だけ短い」となります。
単位量当たりの大きさ(仕事量)を考える問題です。Aだけで作る場合は、1個を作る時間の単位を、そのまま使うことができます。ところが、BとCの2台で作る場合は、2台で1分当たりで作る個数を単位として計算して求めます。そして、最後に題意を考えて微調整を行う必要のある問題でした。
小学校の5・6年で学習する、「単位量当たりの大きさ」は、日常生活でも様々な領域で使われる重要な考え方です。今回の問題は、速さの考え方や仕事算的な考え方ができるかを試す問題です。理解して使うことができるようにしておくことが必要です。仕事に関する特殊算には、仕事算・のべ帰一算・ニュートン算などがあり、その考え方を学習しておきましょう。
仕事に関する特殊算がどのように入試で出題されているのか、そしてそれらを体系的に学習したい方は、以下のブログを参考にご覧ください。
マッキーの算数指導法『特殊算』…『仕事算…その1・中学入試問題《青山学院中等部》』
マッキーの算数指導法『特殊算』…『仕事算…その2・中学入試問題《ラ・サール中学校》』
マッキーの算数指導法『特殊算』…『仕事算…その3・中学入試問題《鴎友学園女子中学校》』
マッキーの算数指導法『特殊算』…『仕事算…その4・中学入試問題《聖光学院中学校》』
マッキーの算数指導法『特殊算』…『のべ算…その1・中学入試問題《江戸川学園取手中学校》』
マッキーの算数指導法『特殊算』…『のべ算…その2・中学入試問題《星野学園中学校》』
マッキーの算数指導法『特殊算』…『のべ算…その3・中学入試問題《海城中学校》』
マッキーの算数指導法『特殊算』…『ニュートン算…その1・中学入試問題《桐朋中学校》』
マッキーの算数指導法『特殊算』…『ニュートン算…その2・中学入試問題《城北埼玉中学校》』
マッキーの算数指導法『特殊算』…『ニュートン算…その3・中学入試問題《渋谷教育学園渋谷中学校》』
マッキーの算数指導法『特殊算』…『ニュートン出題の《ニュートン算》を小学生が解く!』

![]()
ブログ人気投票にクリックいただけると幸いです!
今日は、今年の桜蔭中学入試問題算数の解説・3回目最終回となります。規則性を考えた容積に関する問題Ⅳを取り上げ考えてみましょう。今日の問題は、容積の問題ですが、与えらえた条件から規則性を考えて、数値の大きい計算と単位変換をミス無くこなせば、難しい問題ではありません。
与えられた条件を読み取ることができずに、問題の意味を日ごろ直ぐに聞こうとする姿勢で学習している子どもがいます。入試問題文は、必ずしも上手な言い回しでないことが多いのですが、それでも相手が述べていることを斟酌する力は、大切な能力です。特別なテクニックを用いる問題ではありませんので、正解したい問題です。
【問題】
Ⅳ.直方体の形をした池に噴水があります。池の深さは2mで、底面は1辺の長さが10mの正方形です。噴水は、毎時25分から20分間、池の外から引いてきた水をふき出します。噴水に使う水の水の量は毎分100Lです。また、毎時27分から10分間、池の水を外に流し出します。流し出す水の量は毎分150Lです。
たとえば、9時25分から20分間、噴水は水をふき出します。また、9時27分から10分間、池の水を外に流し出します。これを1時間ごとにくり返します。
ある日の午前7時の水の深さは1mでした。このとき、次の問いに答えなさい。ただし、水の蒸発は考えないものとし、噴水の水はすべて池の中に落ちるとします。また、噴水の水がふき出してから池に落ちるまでの時間も考えないものとします。
(1)この日の午前8時の水の深さ(cm)を求めなさい。
(2)この日の午前10時30分の水の深さ(cm)を求めなさい。
(3)この日は午前11時に雨が降り始めました。雨が降っている間、水面の高さは毎分0.05mmずつ上がっていきます。午後2時35分に雨がやんだとき、池の中の水の量は何Lであるか求めなさい。
【解答・解説】
(1)は、とても基本的な問題です。7時台の水の出入りを、与えられた条件で考えます。
入った水量:100(L)×20(分)=2000(L)
出ていった水量:150(L)×10(分)=1500(L)
増加した水位:(2000-1500)×1000÷(1000×1000)=0.5(cm)
(500Lを1000倍→立方cm、一辺10m=1000cmの正方形の面積でわると、体積÷底面積=高さの計算で、高さ=増加した水位が出ます。)
よって求める水の深さは、100+0.5=100.5(cm)
(2)は、10時30分という水の出入りの途中の時刻の水位を聞いていることが、この問題のポイントとなります。
まず、10時の段階での水位を考えると、(1)で求めたように、1時間あたり0.5cmの水位の上昇が考えられます。すると、100+0.5×3=101.5(cm)
次に10時台の水位の変動を考えるために、水量の増減を計算します。
入った水量:100×5=500(L)
出ていった水量:150×3=450(L)
(500-450)×1000÷(1000×1000)=0.05(cm)の水位の増加となります。
よって、10時30分での水の深さは、101.5+0.05=101.55(cm)となります。
(3)の問題は、考え方は基本的ですが、単位変換や計算を注意しながら解く必要があります。そこで、14時35分までの水の出入りを考えます。
入った水量:100(L)×(20×7+10)(分)=15000(L)
出ていった水量:150(L)×(10×7+8)(分)=11700(L)
入った雨量:1000×1000×0.005×215(分)÷1000=1075(L)
(池の底面積に毎分0.05mm=毎分0.005cmの高さをかけて、さらに雨の降っていた時間215分をかけると、池の中に入った雨量が計算できます。)
よって、14時35分時点での池の中の水の量は、
10×10×1000+15000-11700+1075=104375(L)
この問題も、基本的な考え方で十分な問題です。けれども、下のような単位関係と、式を1本化し分数計算して簡単に行うことが重要です。単位変換ができても、注意深く単位をそろえて式をたてていく必要があります。式を計算して出た数値に単位を付けるという習慣も必要でしょう。
長さの単位:1m=100cm=1000mm
容積の単位:1立方メートル=1kL=1000L、
1L=10dL=1000mL=1000立方センチメートル=1000cc
こうした問題を確実に正解するためには、基本をおろそかにしないで、与えられた条件を理解して、条件と式をきちんとノートに書く、日ごろの学習が必要です。

![]()
ブログ人気投票にクリックいただけると幸いです!
今日は、今年の桜蔭中学校の算数・問題Ⅲを取り上げます。小さい頃に割り箸に図形を張り付けて、それを勢いよく回転させると、割り箸のまわりに、立体図形が出来上がる遊びを経験した方は多いことでしょう。このようにしてできた立体を回転体と言います。
回転体の問題は、出来上がった立体の見取り図を描いてみることが大切です。実際に回転体の見取り図を描かせる入試問題もあります。描いた立体図形が、本来の図形と異なる場合、その体積や表面積を計算しても無論得点にはなりません。
回転させる平面図形から、出来上がる立体図形がどんな図形なのかを理解し、日ごろ見取り図をノートに描いてみる練習が必要です。それも、ある程度素早く図形をかけるように練習しておきましょう。
【問題】
1辺の長さが2cmの正方形を下の図のように、4個、6個、8個、・・・・・・と並べて図形を作っていきます。さらに、できた図形を直線ABのまわりに1回転させて立体を作ります。
(1)正方形を6個並べた図形を直線ABのまわりに1回転させてできる立体の体積と表面積を求めなさい。
(2)立体の体積が11304立方センチメートルとなるとき、もとの図形の正方形の個数を求めなさい。
【解答・解説】
(1)の問題で正方形を6個並べた図形とは、上の図の真ん中の図形です。これを直線ABのまわりに1回転させてできる立体は、下の図の一番左のような図形になります。この図形の体積は、ちょっと工夫して計算すべきでしょう。
下の図のように、三段になっている円柱の一番下の円柱を切り取り、それを中が空洞になっている部分に埋め合わせると、真ん中のような立体となります。同様に二段目の円柱を切り取り、それを中空になっている部分に埋め合わせると、最終的に半径が正方形3個分の6cm・高さが2個分の4cmの円柱になることが分かります。
したがって、求める立体の体積は、ちょっと工夫して計算を簡単にします。
6×6×3.14×4=452.16立方センチメートル
次は、この立体の表面積です。もちろんのこと、体積を求めた変形した図形の表面積を求めても答えは出ません。出来あがった回転体の表面積を求める必要があります。それでも、できるだけ工夫して計算を少なくする必要があります。
この回転体の底面積は、上から見ても下から見ても、半径が6cmの円となりますから、6×6×3.14×2という式で表すことができます。
側面積は、外側の側面積と内側の側面積を合わせて上手く計算しましょう。半径が6cmの円柱の側面積が6×2×3.14×4、半径が4cmの円柱の側面積(外側と内側を合わせて)が4×2×3.14×4、半径が2cmの円柱の側面積が2×2×3.14×4となります。
よって求める表面積は、
6×6×3.14×2+6×2×3.14×4+4×2×3.14×4+2×2×3.14×4
=(72+48+32+16)×3.14
=168×3.14(筆算はこの計算だけ!)
=572.52平方センチメートル
もちろんのこと、一本式で分配の法則を用い、3.14の計算は一回で行います。
この回転体の体積および表面積を求める問題は、基本的な問題ですので、落とすことがあってはならないでしょう。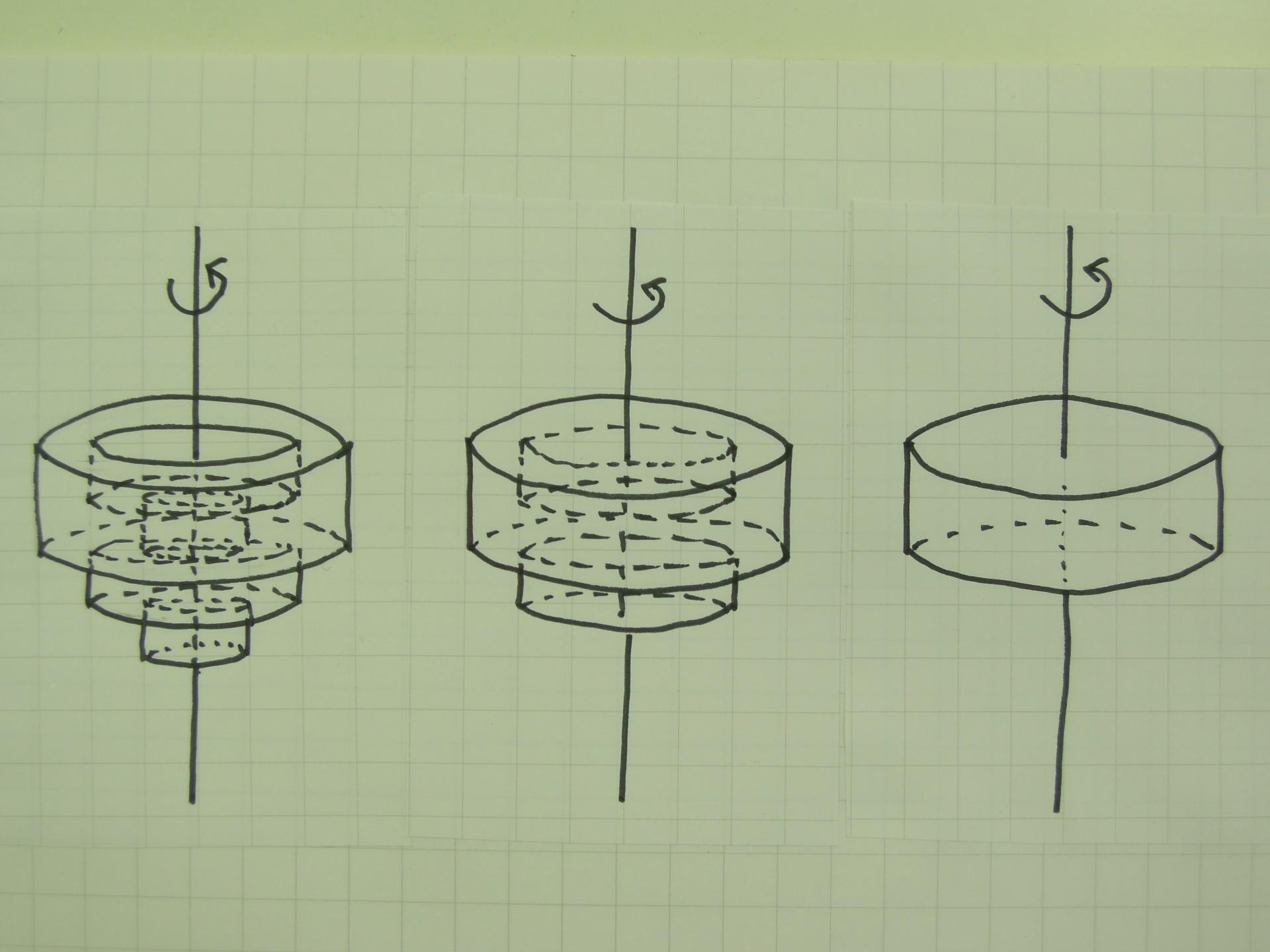
では、(2)の問題です。 正方形が4個の回転体は、(1)の体積を求める時に工夫した考え方を利用すると、半径4cm・高さが4cmの円柱の体積と等しくなります。
この規則性を整理すると、
正方形の数4個・・・・・・円柱の半径4cm 円柱の高さ4cm
正方形の数6個・・・・・・円柱の半径6cm 円柱の高さ4cm
正方形の数8個・・・・・・円柱の半径8cm 円柱の高さ4cm
・・・・・・
そこで、立体の体積が11304立方センチメートルの円柱の高さも、4cmですので底面積を求めます。
11304÷4=2826平方センチメートル
2826÷3.14=900・・・半径×半径の数値
小学生は無論のことルートは使えませんので、こうした問題は必ず平方数になっています。
よって900=30×30ですので、この立体の半径が30cmであることが分かります。
半径の数値と、正方形の個数の数値は、規則性を整理して等しいことが分かっていますから、答えは30個となります。
基本的な考え方を利用して、「ちょっと工夫する問題を解いてみよう」という主旨の出題です。確実に得点したい問題でしょう。そのためにも、展開図・投影図・回転体・転がり移動・回転移動・対称移動などの図形を、日ごろノートにフリーハンドで素早く確実に描く練習をしておくことが必要です。また、計算の工夫で、素早く正確に解答を導き出す練習も大切です。

![]()
ブログ人気投票にクリックいただけると幸いです!
しばらく、今年の中学入試に出題された算数の問題を取り上げ、その傾向と対策について綴っています。今日は、今年の桜蔭中学校の算数の問題を取り上げます。他の女子御三家である女子学院・雙葉中学校に比べて、算数は少し手強い問題が出題されます。男子難関進学校の問題ほど難しい問題ではありませんが、しっかりとした対策をたてて受験する必要があります。
今年の桜蔭の算数は、5つの問題で構成されています。Ⅰ番目の問題は小問形式で、(1)で計算が2題、(2)が群数列の問題、(3)は円の転がり移動の問題で、円が通った部分の面積を求める問題です。
Ⅱは割合を絡めた概数に関する問題、Ⅲは回転体の体積と表面積に関する問題で、工夫して体積を求める考え方ができるかどうかを試す問題となっています。
Ⅳは水の深さに関する問題で、規則性を考えて解く問題です。Ⅴは速さに関する問題で、与えられた条件をしっかりと整理して根気よく解いていく問題です。
今日は、問題Ⅰ(2)の数列に関する問題を取り上げて、説明をしましょう。
【問題】
下の図1のように、小さな正方形の頂点と、大きな正方形の各辺を二等分する点が重なるように、正方形を作っていきます。さらに図2のように、1から小さい順に整数を入れていきます。たとえば、7は一番小さな正方形から数えて3番目の正方形に初めて出てきます。この作業をくり返すとき、次の□にあてはまる数を答えなさい。
①35は一番小さな正方形から数えて□番目の正方形に初めて出てきます。
②一番小さな正方形から数えて51番目の正方形に初めて出てくる4つの数のうち、一番小さな数は□です。
【解答・解説】
一番めの正方形には数字の1が、二番目の正方形には2、3、4、5の数字が、三番目には6、7、8、9の数字が出てきます。
上の問題は、1、(2、3、4、5)、(6、7、8、9)、(10、11、12、13)・・・という群数列の問題として考えます。1組目だけが数字が1個、それ以外は4個の連続した整数でできている群数列です。
①は、35がこの群数列の何組目の数字かを考えます。(35-1)÷4=8あまり2という計算から、35は10組目の数字であることが分かります。注意すべきことは、1が単独で1組目(イレギュラー)で、商の8とあまりの2が示している内容は、35から1を引いた数34が、数字4個を一組として、8組と次の9組目の2番目の数であることです。したがって、35は10組目の数字となるのです。このことから、①の答えの35が出てくる正方形は、10番目となります。
このように考えて、②の問題は、1番目の正方形には数字が1個、2番目から50番目の正方形(49個の正方形)には数字が4個ずつ、そして最後の51番目の正方形に書かれている最初の数字が求める数ということになります。
よって、1+4×(51-1-1)+1=1+196+1=198・・・答えとなります。
こうした問題を日頃練習している受験生にとって、ミスし易いハードルを難なくクリアして解答を導き出すことは、難しいことではありません。数列に関しては、等差数列・階差数列・群数列を中心に、それらの数列を応用した問題が中学入試には出題されます。数の規則性を楽しむように練習してください。また、計算で分数数列の和を求める問題も出題されますが、計算で唯一その解き方を覚えておく必要がある問題です。
数列に関する学習方法について興味のある方は、以下の過去のブログを参考にご覧ください。
数列に関する問題
等差数列の問題
階差数列の基本的問題
マッキーが教える入試問題・算数…群数列の問題
分数の数列の和をどう解くか
マッキーの一問必答:『分数数列の和』の計算
今春の中学入試問題にチャレンジ!…群数列
今春の中学入試問題にチャレンジ!…群数列など

![]()
ブログ人気投票にクリックいただけると幸いです!
マッキーの学習指導法:今年の開成中学入試問題「算数」
マッキーの学習指導法:今年の開成中学入試問題「算数」・・・その2
以上の開成中学の入試問題解説【1】・【2】に続いて、テストの最後の問題・【4】を今日は解説します。飛ばした【3】の問題は、与えられた条件に沿って、書き並べて求める問題で、小問(1)と(2)は簡単な問題です。(3)は時間との勝負の問題ですが、丁寧に書き並べれば正解できる問題です。
【4】の問題は、(1)の曲線の長さを求める問題と、面積に関する問題は、比較的簡単な問題です。しかし、(2)の面積を求める小問は、ちょっとした発想力が要求される問題です。
【問題】(若干実際のテストの言い回しとかえてあります。)
(1)下図において、3つの円の直径AB、AC、ADはすべて6cmで、直線ABと直線ADは垂直です。また、直線ACを線対称の軸とみるとき、点Bと点Dが対応します。点Gは一番左にある円の中心です。
()点Eと点Fとを結ぶ曲線(右図の太線)の長さは何cmですか。
()三角形ABEの面積は三角形EFGの面積の何倍ですか。
()三角形AEFの面積は何平方センチメートルですか。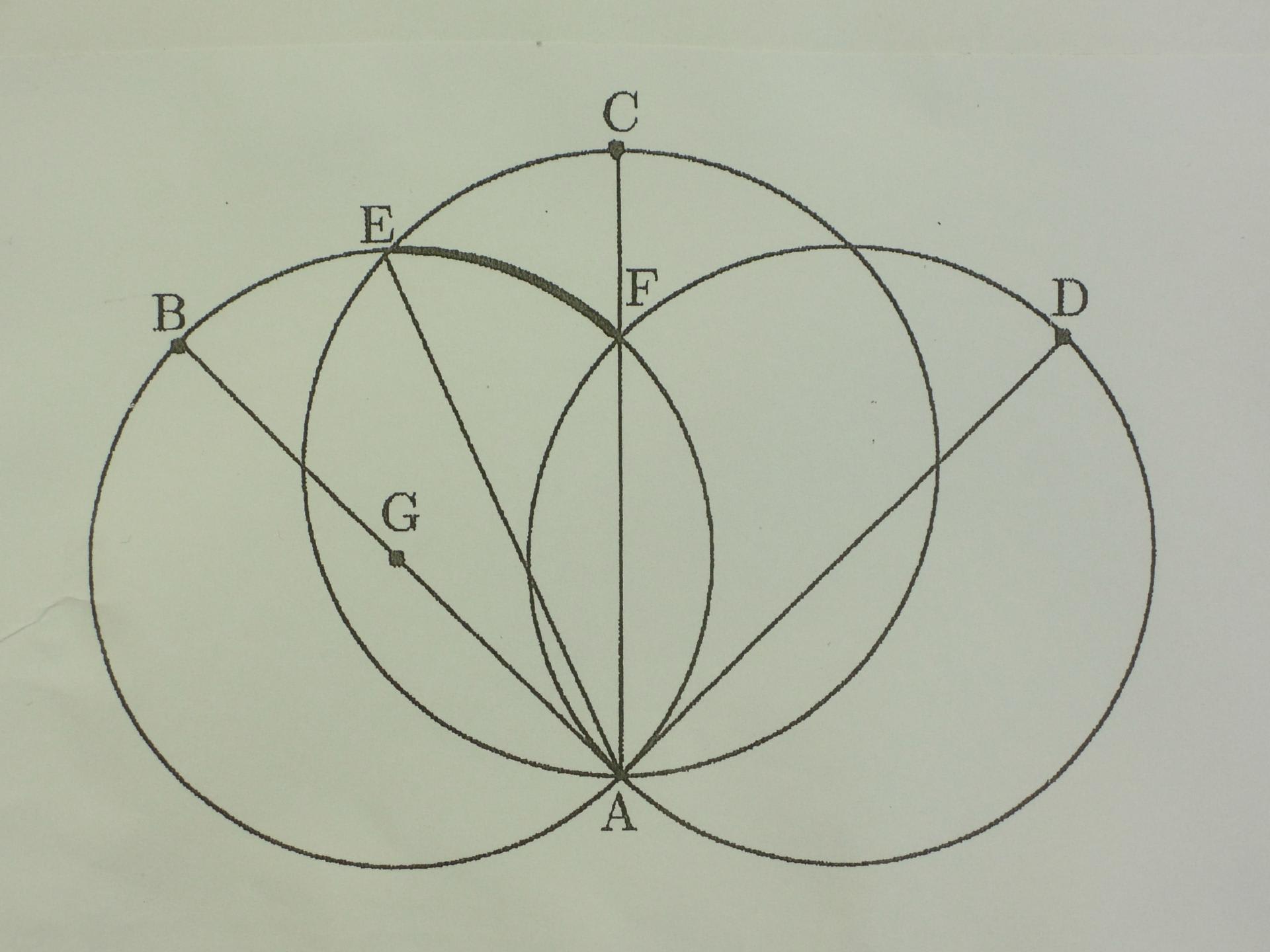
(2)点Oを中心とする半径3cm(直径6cm)の円の周上に、周の長さを8等分する点を取り、順に点P、Q、R、S、T、U、V、Wそれぞれを中心とする半径3cmの円を描くと、下図のようになります。
このとき現れる線を利用して、下図の斜線部の図形を考えます。この斜線部の図形の面積は何平方センチメートルですか。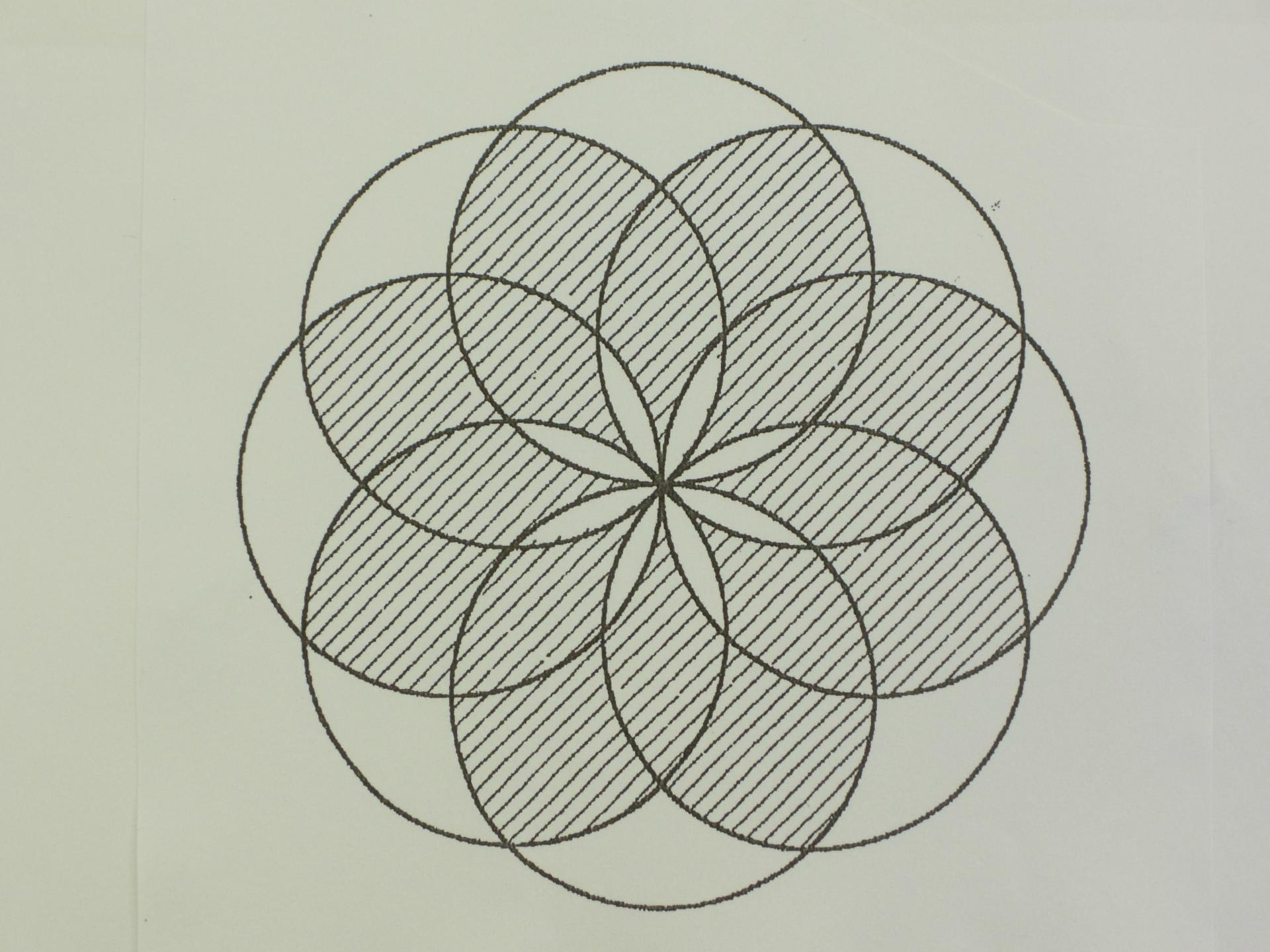
【解答・解説】
(1)の()は、与えられた条件の角BAD=90度から、角BAF=45度、角BGF=90度などが分かり、求める弧EFの中心角が45度となります。よって求める曲線の長さは、6×3.14×45/360=2.355(cm)
()は、まず三角形ABEと三角形BEGを考えると、高さが共通で底辺の長さがAB:GB=2:1ですので、面積の比も2:1となります。三角形EFGは、三角形BEGと合同な三角形です。よって三角形ABEの面積は、三角形EFGの面積の2倍というのが答えとなります。
()は、角BAFと角BGEのそれぞれの角度に注目します。すると角BAF=角BGE=45度ですので、同位角の大きさが等しいので、EGとFAは平行になっていることが理解できます。そこで、三角形AEFの頂点Eを点Gまで移動して、等積変形した三角形AGFを考えます。三角形AEF=三角形AGFとなりますので、直角二等辺三角形の三角形AGFの面積を計算して、求める三角形AEFの面積とすることができます。よって、3×3÷2=4.5平方センチメートルが答えとなります。
(2)この問題は少々難解です。複雑な図形の面積を求める場合、①この図形を分けて考える、②この図形を含む図形から余分を引く、③等積変形・等積移動を使う、④規則性を考える、などの方法が考えられます。この問題は、④の方法を使って考えると、比較的簡単に解くことができます。求める斜線部分の面積は、太線で囲まれた図形が8個組み合わされた図形として捉えて、面積を計算します。
中にある花弁状の8つの白い部分に、外周の小さな弓型を切り取り、等積移動して求める方法もあります。いずれにしろ、面積を求める図形を、より小さな合同な図形の集合体とし、等積移動などを用いて計算できる図形に変換することで、求める問題です。

太線で囲まれた一つの図形は、大小二つの弓形の部分を切り取り等積移動すると、平行四辺形となります。この平行四辺形の半分の面積が、(1)の()で求めた三角形AEFと合同ですので、面積(4.5平方センチメートル)が等しくなります。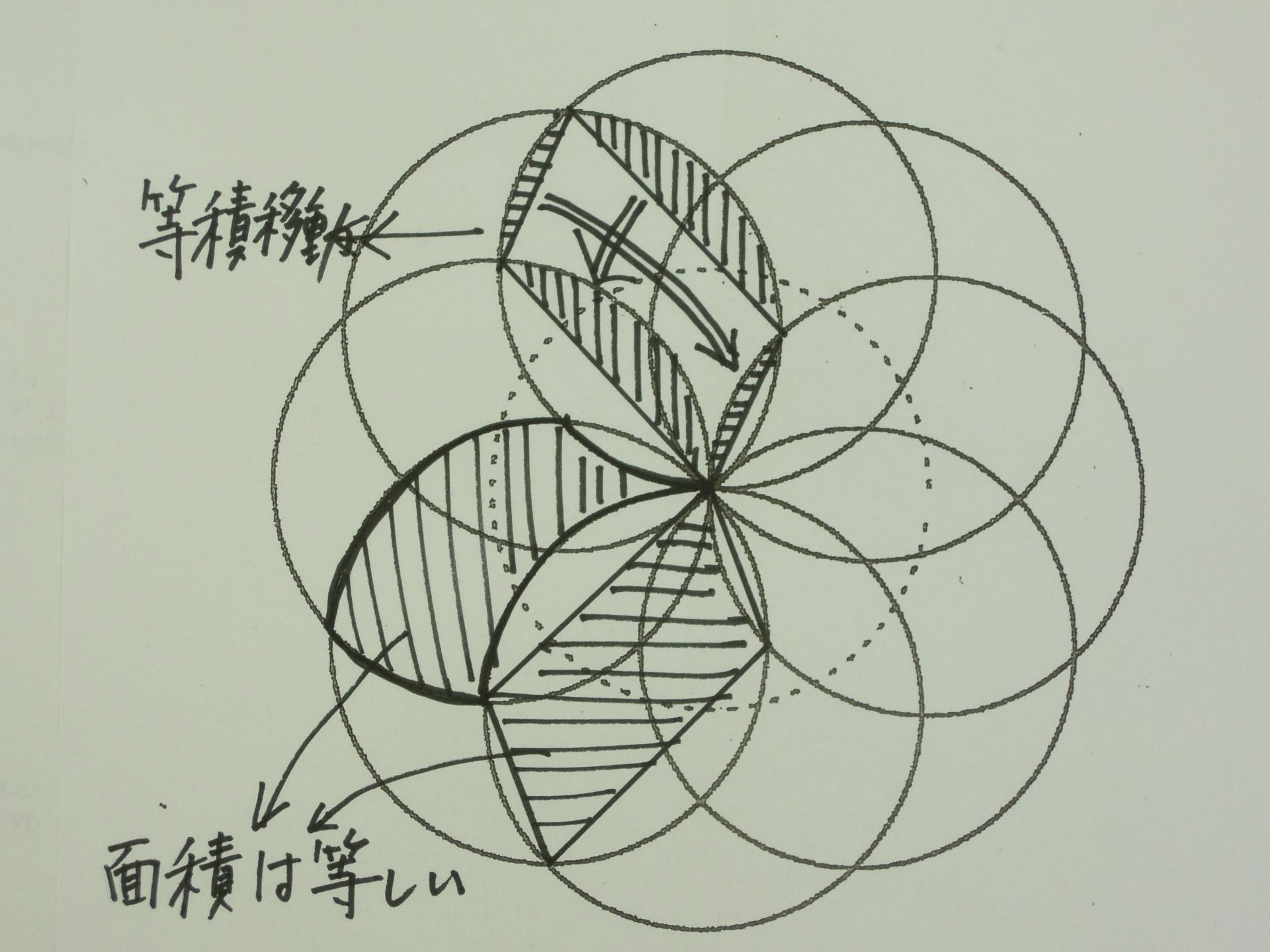
よって求める斜線部分の面積は、4.5×2×8=72(平方センチメートル)と、チョ~簡単に計算できます。
回転移動・転がり移動・対称移動や、回転体・展開図・投影図・図形の切断などの図形の問題を解くためには、日頃の学習の中で、図形をノートに手書きして考えることが必要です。苦手意識を持たずに、面倒がらずに取り組んでいくことが大切です。
トップ校あるいは上位校の算数は難しいと言われています。しかし、合格するためには100点をとる必要はないので、開成の算数さえ、確実に得点できる問題が7割ほどありますので、ここでしっかりと得点する学習を日ごろ心掛けることが大切です。また、算数を得点源とする受験生は、今回の解説で難しいと指摘した問題も、果敢にチャレンジする学習が必要でしょう。

![]()
ブログ人気投票にクリックいただけると幸いです!
『マッキーの学習指導法:今年の開成中学入試問題「算数」』に続いて、今年の開成中学の入試問題を取り上げ、出題意図を含め、受験対策に役立つ解説をしましょう。多くの受験生が、トップ校を受験するわけではありませんが、トップ校の入試問題には、受験生が学ぶべきポイントが象徴的に取り上げられていますので、指導する保護者の皆様には、とても参考になると思います。
前の問題は、開成中学の算数入試問題の【問題1】を取り上げました。今日は、「仕事算」や「単位量あたりの大きさ」などの考え方と、割合の考え方を用いて解く【問題2】について取り上げましょう。取り上げる入試問題は、私なりの解き方で説明しますが、上位校の算数の解法は幾通りか考えられます。その中でも分り易い解き方を説明することにします。
【問題2】
3人の職人A、B、Cの1日あたりの賃金はそれぞれ6000円、9000円、30000円です。ある仕事をA1人に頼むと600日、B1人に頼むと400日、C1人に頼むと200日でちょうど完了します。職人が2人、あるいは3人で同じ日に作業したとき、それぞれの能率は1人のときと変わらず、その合計の作業がされます。また、最後の日は途中で仕事が完了しても1日と数え、1日分の賃金を支払います。以下の問いに答えなさい。
(1)どの日も、A、B2人だけで作業すると、この仕事は何日で完了しますか。
(2)210日以内にこの仕事を完了させるとき、賃金の合計金額が一番少ないのは、A、B、Cそれぞれに何日ずつ頼むときですか。また、そのときの賃金の合計金額はいくらですか。
(3)賃金の合計金額を420万円以内とするとき、この仕事が完了するまでにかかる日数が一番少ないのは、A、B、Cそれぞれに何日ずつ頼むときですか。また、そのとき何日で仕事は完了しますか。
【解答・解説】
最初の(1)の問題は、いわば仕事算の基本的な問題として解くことができます。仕事算とは、全体の仕事量を1と置き、それぞれの単位時間あたりの仕事量を求めて解く問題のことを言います。この問題であれば、Aの一日あたり(単位時間)の仕事量は、1/600、Bの一日あたりの仕事量は1/400です。
よって求める日数は、1÷(1/600+1/400)=240(日)・・・(1)の答え、と出すことができます。これは、とても簡単な問題です。予習シリーズでは、こうした問題を、最小公倍数を使って整数計算させていますが、計算は簡単になりますが、子どもたちが全体を見積もって解いていくことができないので、あまり良い解き方とは言えません。
次は(2)の問題です。(1)で求めたように、AとB二人だけでは、この作業が終わるのに240日かかってしまいます。したがって、AとB二人で210日働き、残りの作業をCにやってもらった時、『賃金の合計金額が一番少ない』という条件を満たすはず。
よってCが働く日数は、{1-(1/600+1/400)×210}÷1/200=25(日)・・・Cの日数
考え方で説明した通り、AとBはそれぞれ210日。
賃金の合計金額=(6000+9000)×210+30000×25=3900000(円)
この問題も比較的考えやすい問題です。
最後の(3)の問題です。A、B、Cの働く日数をそれぞれA、B、Cと置いて、与えられた条件を文字式で整理してみましょう。
作業(仕事)の量の関係から、1/600×A+1/400×B+1/200×C=1・・・①
賃金の合計金額を420万円以内という条件から、
6000×A+9000×B+30000×C=4200000・・・②
(小学生は不等式が解けないので、一応420万円として計算します)
①を簡単にして、2×A+3×B+6×C=1200
②を簡単にして2×A+3×B+10×C=1400
中学生では、三元一次方程式ですが、小学生では消去算と呼びます。
4×C=200
C=50(日)
上の式にC=50を代入すると、2×A+3×B=900となります。不定方程式のようですが、2人が一緒に連続的に作業を進める時が、『仕事が完了するまでにかかる日数が一番少ない』という条件を満たしますので、A=Bと考えます。
よって、2×A+3×A=900 5×A=900 A=180(日)
以上のことから、A180日、B180日、C50日となり、180日でこの仕事が完了するというのが(3)の答えとなります。
仕事算的な考え方ができること。また、与えられた条件を理解して、文字式等で条件を整理することができることが、この問題を解く条件となります。けれども、問題の意味を理解できれば、比較的解き易い問題と言えるでしょう。

![]()
ブログ人気投票にクリックいただけると幸いです!
難関中学を含めた中学受験に合格するためには、合格者と不合格者の得点の乖離が最も大きい科目である算数で、しっかりと得点することが重要です。男子上位進学校の算数が、その中でも最も難しいと言われていますが、それでもフィギアスケートでトリプルアクセルを跳ぶ離れ業のような問題ではありません。
トップ校の算数を解くためには、基本的な考え方をしっかりと理解して、それを様々な問題に応用できる「身に付いた知識」にまで高めておく必要があります。また、基本的計算力を駆使して、ミスなく解答を導き出す注意力が大切です。
また最近では、頭脳に汗して書き並べていく、根気強さも要求されるようになりました。規則性を見つけ出す発想力も要求されています。
では、今年のトップ校の入試問題を使って、その問題の出題意図を含め、受験対策に役立つ解説を、数回にわたり伝授したいと思います。ただし、取り上げる入試問題は、私なりの解き方で説明しますが、上位校の算数の解法は幾通りか考えられます。その一つの解き方を説明することになります。
まずは、今日は私立中学の雄・開成中学の問題です。大きな問題が4題出題され、それぞれ小問3~4題で構成されています。問題1は、速さに関する問題。問題2は、割合に関する問題。問題3は、規則性の問題で、書き上げて考える問題。最後の問題4は、円に関する長さや面積を求める問題で、最後の4番目の小問の求積問題が、ちょっとした発想力が必要な問題となっています。
それぞれの小問の内、最後の小問を除きさほど難しい問題ではありません。したがって、そうした問題を完全に正解することが必要ですが、100点をとる必要はないので、最後の小問を捨てても、しっかりと見直して正解する戦法もあります。算数を得点源にする受験生は、最後の小問も意欲的に解く必要があります。
【問題1】
2つの地点X、Yを結ぶ道があります。A君はXからYへ向かって、B君はYからXへ向かって移動し、地図上の中間地点Mで出会うことにしました。地図には等高線が描かれていなかったため、B君は、図1のように2人とも水平な道を移動すると考えました。B君は、自分がA君より速く移動できること、おのおのがつねに同じ速さで移動することの2つをふまえて、A君が出発してから15分後に出発しました。これで、2人はちょうどMで出会うはずでした。
ところが、実際には図2のような下り坂がありました。X%の下り坂では移動する速さがX%だけ増すことになります。ここで下り坂がX%であるときは、
X=(下向きに移動する長さ/横向きに移動する長さ)×100(実際の表記とは異なる)
のことを指します。それでも無事に、2人はちょうどMで出会いました。このとき、以下の問いに答えなさい。なお、3辺の長さの比が3:4:5や5:12:13となる直角三角形を利用してもかまいません。
(1)①A君がXを出発してからMでB君に出会うまでに、「実際にかかった時間」は、「事前にB君が想定していた時間」の何倍ですか。
(2)②B君がYを出発してからMでA君に出会うまでに、「実際にかかった時間」は、「事前にB君が想定していた時間」の何倍ですか。
(2)A君がXを出発してからMでB君に出会うまでに「実際にかかった時間」を求めなさい。
【解答・解説】
グラフを見ると、道のりが平坦ならX地点とY地点から中間地点Mまで、16目盛りあります。A君が平坦な一目盛りを歩く時間を1と仮定します。すると、B君が想定したA君のMまでの到達時間は、16÷1=16ということになります。
ところが実際のMまでの道のりは、下り坂が10と平坦な道が8でした。そこで、まず下り坂10の道のりを進む時間を計算します。
下り坂で速さの増す割合は、下向きに移動する長さ/横向きに移動する長さ=6/8=3/4ですので、A君の下り坂の速さは、1+3/4=7/4となります。よって、A君のMまでの実際の時間は、10÷7/4+8=96/7となります。
よって求める割合は、96/7÷16=6/7・・・①の答え、と出すことができます。
B君もA君と同様に求めます。B君はA君よりも速いのですが、計算上B君の速さも一目盛り進む速さを1とすると、想定到達時間は16となります。実際の道のりは、下り坂13と平坦な道4となっています。
条件に従い、下り坂で速さの増す割合を求めると、5÷12=5/12となります。よってB君の下りの速さは、1+5/12=17/12となります。この数値を使い、下り坂13と平坦な道4の実際の時間は、13÷17/12+4÷1=224/17となります。
よって求める割合は、224/17÷16=14/17・・・②の答え
さて、ここまでは順調に解けましたか?計算ミスしなければ、さほど難しい問題ではありません。最後の問題が解けるかどうか。
そこで、ここまで出て来た条件を整理しましょう。
A君の想定していた時間をA(分)と表し、B君の想定していた時間をB(分)と表すと、次のような文字式で整理することができます。上位校を目指す場合、小学生でも「条件を文字式で整理」することは大切です。(求めるA君の「実際にかかった時間」をAとして、式をたてることはできません。)
A-B=15(分)・・・初めの想定時間差
A×6/7-B×14/17=15(分)・・・実際も時間差は同じだった
この消去算の式を解くことにより、A君とB君の想定した時間を求めることができます。
この文字式を解くことを、小学生では「消去算」と呼びますが、中学生では「連立二元一次方程式」となります。そこで、公立中学1年で学習する一元一次方程式と、中学2年の連立方程式は、解けるようにしておくことが必要です。
この式を計算すると、A=315/4 (B=255/4)と出ます。
よって求める「A君が実際にかかった時間」は、①で出した割合を利用して、315/4×6/7=135/2(分)と出すことができました。よって、1時間7分30秒・・・(2)の答え。
四谷大塚の予習シリーズでは、割合のつるかめ算などというピンとのずれたタイトルで指導していますが、「消去算」として教えた方が妥当な問題です。
開成中学算数の入試問題でも、小問3題中、2題が比較的解き易い問題で構成されています。合格するためには、その2題を落とさない学習が必要でしょう。このシリーズでは、トップ校の算数を取り上げ、日ごろの学習法を伝授します。

![]()
ブログ人気投票にクリックいただけると幸いです!
今日は、塾で小学校5年生が学習する水溶液と金属の反応についての学習を取り上げます。金属は、酸やアルカリに反応します。代表的な塩酸と水酸化ナトリウムが、亜鉛・アルミニウム・鉄・銅などの金属にどう反応するのかを勉強します。まず、学習した問題を取り上げます。皆さんも問題の内容を読んで、ちょっと考えてみてください。
【問題】
アルミニウム・鉄・銅の粉と、これらの粉のうち2種類を混ぜた粉・3種類すべてを混ぜた粉を用意しました。これらの粉の中から5種類を選んでいろいろな量をとり、十分な量の塩酸と水酸化ナトリウム水溶液に溶かしました。その後、溶け残った粉を乾燥させて重さを測りました。(図1)は塩酸、(図2)は水酸化ナトリウム水溶液に溶かしたときの結果で、A~Eがそれぞれの粉を示しています。これについて、次の問にそれぞれ記号で答えなさい。
(1)1種類の粉だけだったものはどれですか。
(2)銅の粉が最も多くふくまれていたものはどれですか。
(3)銅とアルミニウムだけを混ぜた粉はどれですか。
(4)アルミニウムが同じ量だけふくまれていた粉はどれとどれですか。
(5)3種類を混ぜた粉はどれですか。
さて、大人でもこの問題文と2つの図を見て、問題の内容を理解することは簡単ではありません。この問題を解くための知識は、基本的なことですが、まず図を読み取る作業からスタートしなければなりません。最近の中学入試の算数問題では、条件を具体的に提示せずに、グラフなどから読み取ることからスタートさせる問題が増えています。
この問題は、まずアルミニウム・鉄・銅の3種類の粉から、単一な金属だけで3種類、2つの金属を混ぜた粉は「組み合わせ」の考えで3種類、3つの金属を全て混ぜた粉は1種類の計7種類の粉を作ることができることを、押えておく必要があります。
この問題は、作った7種類の粉から5種類の粉を選び、これらの金属が酸とアルカリに完全に反応するように、「十分な量」の塩酸と水酸化ナトリウムに溶かした結果を図で表しています。溶け残った粉とは、塩酸あるいは水酸化ナトリウムに反応せずに溶けずに残った金属の粉です。間違えてはいけないのは、水溶液の水分を蒸発させたのではなく、溶け残った金属をろ過して得られた量を表していることです。ろ液の中には、当然溶けた金属(イオンになった)が入っています。
この問題は、アルミニウム・鉄・銅が、塩酸と水酸化ナトリウムとどう反応するかを理解しているかどうかを調べる問題といえるでしょう。塩酸は、アルミニウムと鉄を溶かし銅を溶かすことができません。水酸化ナトリウムは、アルミニウムを溶かすことができますが、鉄と銅を溶かすことができません。
ただこの知識を持っていても、複雑に構成された問題をしっかりと読んで、問題の意味を理解することは容易ではありません。したがって、漠然と問題を読んでも与えられた条件を理解できませんので、条件を視覚的にまとめることが重要となります。
算数の文章題を代表として、こうした問題を解く場合、問題条件を上手く整理する力を日頃養成しているかどうかが、問題を正解できるか否かの条件となります。大人でも今回のような問題の文章を読んでいるだけでは、何のことか理解できずに、紙と鉛筆が必要になることでしょう。
私は、生徒に理解させるために、下のような表にまとめました。すると、この実験のポイントが視覚的に見えてくるはずです。
二つの図から、上のような表が完成します。この表から見えてくるもの・・・、基本的な知識があれば、この表を参考にして、問題を解くことができます。
例えば、AとBは、塩酸に入れると、全て溶けて0gとなっていることから、銅の粉がふくまれていない事が分かりますので、銅の表に☓を付けます。反対にCとDとEは、塩酸に入れると、それぞれ4g・5g・3g残りますから、この数値がふくまれていた銅の量ですので、銅の表に○を付けます。
Aの粉には、アルミニウムと鉄がふくまれますが、水酸化ナトリウムに溶かすと、1g溶け残りますが、それが鉄の量です。Aの粉には、アルミニウム5gと鉄1gがふくまれていることが分かります。Bの粉は、アルミニウムと鉄を含む可能性がありますが、水酸化ナトリウムに溶かすと全量2gが全て溶け残っています。したがってBは、鉄2gの単一な粉であることが分かります。
この表を参考に、同様な判断を下して、上のような表を完成させます。ふくまれるか否かの判定だけではなく、金属別の量も導き出すことができます。基本的な知識があれば、かなり素早くこの表を書き上げることができます。そしてこの表を見ながら、問題の(1)から(5)までを正解することができます。単に問題文と図を見ていただけでは分からなかったことが、条件を整理すると視覚的にすっきりと内容を把握することができます。
学習における問題を解く場合に限らず、日常に起きるさまざまな問題解決に、与えられそして読み込める条件を整理することが、とても重要です。小学生が算数の問題を解く時に用いる問題条件整理法を、近々まとめてこのブログで綴ります。
おっと、今回の問題の正解ですか?・・・私が整理した表と、金属の酸・アルカリとの反応の説明をチェックすれば、鉛筆片手に正解することができるはずです。そこで、あえて正解は載せませんので、どうぞ皆さんパズルとしてこの問題を解いてみてください。

![]()
ブログ人気投票にクリックいただけると幸いです!
「一問必答」は、「一問一答」に掛けた造語として、今回のシリーズで用います。中学受験した学校に合格するために、ぜひ正解してほしい問題の中で、特に経験的に修得すべき基礎的知識を含む26年度の問題を取り上げ、ポイントを解説します。今回で、このシリーズは、いったん終了します。
半径が出ていないのに、円の面積が求まるの?中学の三平方の定理が分からないのに、どうやって半径を求めるの?そんな疑問が浮かぶ問題です。こうした問題を解くポイントは、半径が出ていなければ、半径×半径の数値が出せるかどうかを考えます。この解き方は、やはり経験的に覚えることが大切です。
このパターンの問題は、円と正方形が絡んで出題されます。正方形の面積は、一辺×一辺で求めることができますが、正方形はひし形の仲間ですから、対角線×対角線÷2でも計算することができます。このことをうまく使って、半径が出ていなくとも、半径×半径の数値を導き出して考える問題です。
【26年度の入試問題】 (分数の表記および記号が、実際の入試問題と若干異なります。)
1.東邦大学付属東邦中学校
この年の東邦大東邦の算数の問題は、問題1が計算3題、問題2が小問3題、問題3から問題7までが小問2~3題で構成された大問の出題でした。今回の問題は、問題2の小問として出題された問題です。
【問題】
下の図のように、正方形ABCDの4つの頂点を通る円がある。また、点E、F、G、Hはそれぞれ辺AB、BC、CD、DAのまん中の点である。この円の面積が10㎠であるとき、四角形EFGHの面積を求めなさい。ただし、円周率を3.14とし、小数第2位を四捨五入して答えなさい。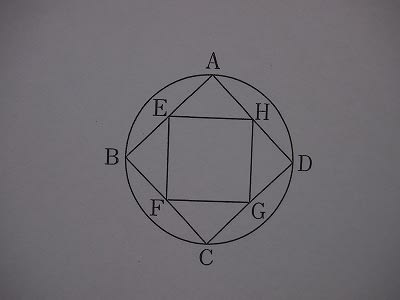
2.江戸川女子中学校
この年の江戸川女子の算数は、問題1では計算4題を含む小問13題、問題2から問題4まで小問3題で構成された入試問題でした。今回の問題は、問題1の小問として出題された問題です。
【問題】
下の図のように、1辺の長さが10cmの正方形と4分の1円があります。円周率を3.14とすると、車線部分の面積の合計は□㎠です。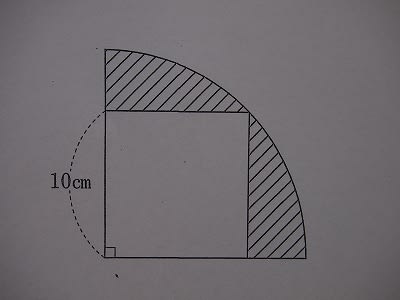
3.ラ・サール中学校
ラサールのこの年の算数は、問題1が計算3題、問題2が小問4題、問題3から問題6までが小問2~3題で構成された大問でした。今回取り上げた問題は、問題2の小問の一つとして出題された問題です。
【問題】
対角線の長さが10cmの正方形Aがあります。その一辺を半径とするおうぎ形Bと、対角線を半径とするおうぎ形Cを右の図のように作ります。
(ア)2つのおうぎ形の面積の比を求めなさい。
(イ)2つのおうぎ形の面積の差を求めなさい。円周率は3.14とします。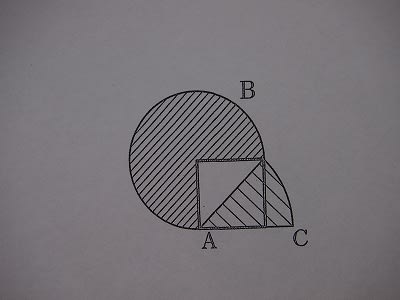
【解答と理解しておくべきポイント】
1.東邦大学付属東邦中学校
小さい時から、折り紙をしている方はすぐに分かるでしょう。正方形ABCDの面積が出れば、その半分が正方形EFGHの面積となります。
円の面積は出ていますが、円の半径は出ていません。正方形ABCDの一辺の長さも出ていません。そこで、この正方形の面積を、対角線×対角線÷2=直径BD×直径AC÷2ということに注目して求めることを考えます。
直径=半径×2ですので、正方形ABCDの面積=直径BD×直径AC÷2
=半径×2×半径×2÷2=半径×半径×2と変形することができます。
円の面積=半径×半径×3.14=10(㎠)から、
半径×半径=10÷3.14=約3.18と導き出すことができます。ここで、半径の長さを求める必要はありませんし、小学生が求めることもできないはずです。
この数値を使って、正方形ABCDの面積=半径×半径×2=3.18×2=6.36
よって求める正方形EFGH=6.36÷2=3.18
少数第二位を四捨五入して、求める面積は3.2(㎠)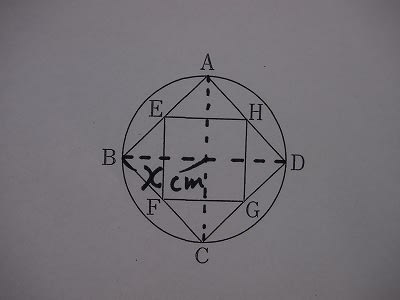
2.江戸川女子中学校
斜線部分の面積は、四分円の面積から正方形の面積を引いて求めることができます。正方形の一辺の長さは出ていますが、円の半径は出ていません。
円の半径は、正方形の対角線の長さと一致しています。このことを利用して円の面積を求めます。
まず正方形の面積は、一辺×一辺=10×10=100(㎠)
また、対角線の長さをXcmとすれば、
正方形の面積=対角線×対角線÷2=X×X÷2=100でもありますから、
X×X=200・・・このことから半径×半径=200であることが分かります。
よって求める斜線部分の面積は、半径×半径×3.14÷4−正方形の面積となり、
200×3.14÷4−100=157−100=57(㎠)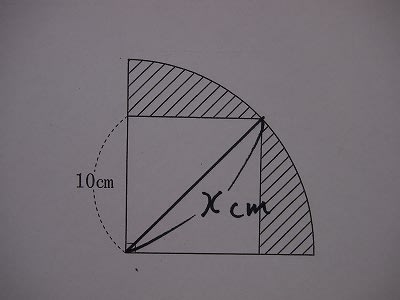
3.ラ・サール中学校
(ア)2つのおうぎ形の面積の比を求める。
おうぎ形Bの面積は、半径×半径×314×270/360で求めることができます。
また、半径×半径は正方形の面積と一致しますから、その数値は、10×10÷2=50となります。
よって求めるおうぎ形BとCの面積比は、
(50×3.14×270/360):(10×10×3.14×45/360)
=50×3/4:100×1/8
=3:1
(イ)2つのおうぎ形の面積の差を求める。
これは、前の問題の(ア)ができれば簡単です。
おうぎ形B−おうぎ形C
=50×3.14×270/360−10×10×3.14×45/360
=(37.5−12.5)×3.14
=25×3.14
=78.5(㎠)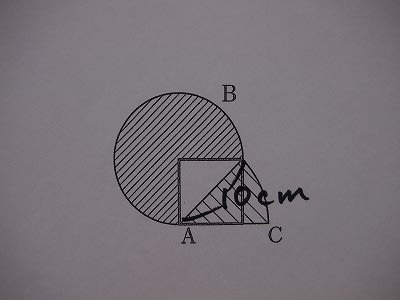
円の面積を求める問題で、半径の長さが出ていないとき、半径×半径の数値が出せるかどうか考えて解く問題でした。この解き方も、日常の学習で経験的に習得すべき考え方です。
最新の中学入試問題を使い、こうした経験的に理解しておくポイントを含む問題を取り上げ、13回にわたって説明してきました。難しい問題ではありませんが、出題頻度も高く、理解していないと解く手がかりが掴めない問題です。
2月上旬の中学入試、そして3月2日には都立高校の合格発表、続いて国立大学の合格発表があり、今年の受験シーズンは終了します。今度は、今年度入試問題が出そろった頃に、問題を分析して、別の視点から合格のためのアドバイスをしたいと思います。

![]()
ブログ人気投票にクリックいただけると幸いです!
「一問必答」は、「一問一答」に掛けた造語として、今回のシリーズで用います。中学受験した学校に合格するために、ぜひ正解してほしい問題の中で、特に経験的に修得すべき基礎的知識を含む26年度の問題を取り上げ、ポイントを解説します。
今日のテーマは、図形の重なった部分を考慮して考える問題です。この問題は、多くの学校で出題される基本的な考え方で、しっかりと学習しておく必要のある問題です。
【26年度の入試問題】 (分数の表記および記号が、実際の入試問題と若干異なります。)
今回のタイプの入試問題から、公文国際学園中等部・共立女子中学校・女子学院中学校の3校の問題を取り上げ、その考え方を解説します。
1.公文国際学園中等部
公文国際の算数は、問題1が計算を含む小問10題、問題2がやはり小問5題、問題3は同様に小問4題で構成されています。問題4は平面図形4題、問題5は小問4題で構成された大問です。今回の問題は、問題1の小問の一つです。
【問題】下の図は半円と直角三角形を組み合わせたものです。2つの車線部分の面積が等しいとき、BCの長さは□cmです。ただし、円周率は3.14とします。 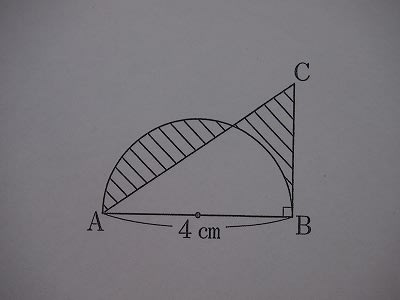
2.共立女子中学校
共立の26年度算数は、問題1が計算を含む小問7題、問題2が円柱の展開図に関する作図、問題3から問題7までが小問2題で構成された大問といった出題でした。今回の問題は、問題1の小問の一つとして出題されました。
【問題】下の図は、おうぎ形と直角三角形を重ねたものです。2つの車線部分の面積が等しいとき、aの長さは何cmですか。 
3.女子学院中学校
26年度の女子学院の算数は、問題1が小問5題で構成され、その後に大問が7題続きます。割合の問題・立体図形の展開図に関する問題・容器に水を満たすグラフ読み取りの問題・図形の転がり移動の問題・仕事に関して周期算を用いる問題・条件整理の問題などの内容で大問は出題されています。今回解説する問題は、問題1の小問の一つです。
【問題】図のように、1辺が11cmの正方形を2本の直線で4つの部分に分けたら、四角形ABCDと三角形CEFの面積が等しくなりました。辺ABの長さは□cmです。 
このシリーズで取り上げる今春の中学入試問題は、私が作成した解説および解答を見ずに、まずは自力で解いてみることをお勧めします。大人には頭の体操になりますし、また受験生は、算数に対する興味や面白さが、倍増するはずです!
【解答と理解しておくべきポイント】
1.公文国際学園中等部
問題の条件から、斜線部分のアとイの部分の面積が等しいことが分かります。
ア=イ
そこで半円と直角三角形の重なった部分ウを加味して考えると、
ア+ウ(半円の面積)=イ+ウ(直角三角形の面積)
直角三角形の面積=半円の面積から、4×□÷2=2×2×3.14÷2
よって、□=3.14(cm)
2.共立女子中学校
条件から、ア=イ
重なった部分を加えて、四分円=直角三角形となり、ア+ウ=イ+ウ
6×a÷2=6×6×3.14÷4 これを解いて、a=9.42cm
3.女子学院中学校
与えられた条件から、ア=イ
台形と直角三角形の重なった部分ウを加えて考えると、
台形の面積=直角三角形となり、ア+ウ=イ+ウ
(AB+2)×11÷2=6×11÷2
この式を解いて、AB=4cm
斜線部分の面積が等しいという条件を、もう少し広い視野で考えて、重なった部分(共通部分)まで加えると比較的簡単に問題を解く事ができる問題です。こうした考え方は、算数に留まらずさまざまな状況で使える見方を含んでいます。

![]()
ブログ人気投票にクリックいただけると幸いです!
「一問必答」は、「一問一答」に掛けた造語として、今回のシリーズで用います。中学受験した学校に合格するために、ぜひ正解してほしい問題の中で、特に経験的に修得すべき基礎的知識を含む26年度の問題を取り上げ、ポイントを解説します。
前回2回にわたり、二等辺三角形の性質を利用した、角度の問題を取り上げました。今回取り上げる問題は、知識として持っていないと、難解に感じる問題です。特別な角度が出てきたら、それを使って考える方法を知っていることが重要です。
【26年度の入試問題】 (分数の表記および記号などの表記が、実際の入試問題と若干異なります。)
特殊な角度に着目して考える問題は、多くの学校で出題されていますが、今回は、跡見学園中学校・田園調布学園中等部・東京女学館中学校・豊島岡女子学園中学校の4校の26年度入試問題を取り上げます。
1.跡見学園中学校
跡見の26年度算数入試問題は、1番目の問題は計算と時間の単位変換の問題が4題、2番目が小問6題、その後に小問3題でできた大問2題という構成です。今回の問題は2番目の小問の一つです。
【問題】下の図の平行四辺形ABCDの面積を求めなさい。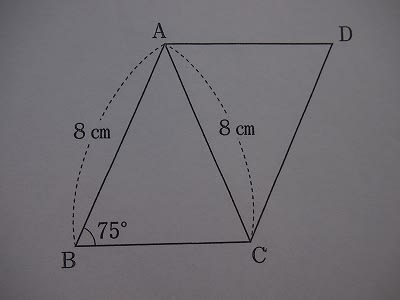
2.田園調布学園中等部
26年度の田園調布の算数は、1番目の問題が小問10題で構成され、その後に小問2~3題によってできている大問が4題で出題されました。今回の問題は、1番目の問題の小問です。
【問題】図のように、おうぎ形の中心Oが点Bに重なるように折ったところ、角アの大きさが90度になりました。角イの大きさを求めなさい。
3.東京女学館中学校
26年度の算数は、最初の問題が計算4題、2番目が小問6題、その後に大問5題の構成です。今回取り上げた問題は、2番目の小問の一つです。
【問題】下の図のように6つの同じ大きさの正方形を並べ、2本の直線をひきました。角アと角イの大きさを合計した角度を求めなさい。
4.豊島岡女子学園中学校
26年度の豊島岡女子の算数は、1番が計算を含む小問4題、2番が同様に小問4題、その後に大問4題という構成です。今回の問題は、2番の小問の一つです。
【問題】下の図の四角形ABCDはAB=AD、AC=10cmです。角ACBの大きさは15度であり、角ABCの大きさと角ADCの大きさの和は180度です。このとき、四角形ABCDの面積は何㎠ですか。
このシリーズで取り上げる今春の中学入試問題は、私が作成した解説および解答を見ずに、まずは自力で解いてみることをお勧めします。大人には頭の体操になりますし、また受験生は、算数に対する興味や面白さが、倍増するはずです!
【解答と理解しておくべきポイント】
1.跡見学園中学校
この問題は、底角が75度の二等辺三角形という特殊な条件に注目します。この頂角の大きさは、
180−75×2=30(度)と出すことができます。
頂角30度の二等辺三角形で、等しい辺の長さが出ていると、この二等辺三角形の面積を求めることができるのです。これは基本事項であり、知っておく必要があります。
この類題で、半径が8cmの円に内接する正十二角形の面積を、同様にして求める問題も出題されます。
角Bから辺ACに垂線を引き、その交点をEとすると、三角形ABEは角が30度・60度・90度の特殊な三角形(三角定規)になります。よって、AB:BE=2:1となり、BEの長さは4cmと出てきます。
三角形ABC=8×4÷2=16 求める平行四辺形の面積は、16×2=32㎠
2.田園調布学園中等部
まず三角形AOBにおいて、折り返した辺なのでAO=AB、また辺OBは半径なので、AO=AB=OBとなり、三角形AOBは正三角形であることが分かります。
また、三角形DBOにおいて、折り返した辺ですからDO=DBで、角ODB=90度という条件から、三角形DBOは直角二等辺三角形です。
ここまで気づくと、あとは簡単!
角イ=角AOB+角BOD=60度+45度=105度
3.東京女学館中学校
下の図のように、一本の補助線を引きます。するとこの三角形が直角二等辺三角形になっていることが分かるでしょうか。
そして、角アの錯角と角イの錯角の合計が、この直角二等辺三角形の底角になっていることに気づけば、この問題を簡単に解くことができます。
角アも角イもそれぞれ何度かは分かりませんが、その二つの角の和は45度であることは分かります。
4.豊島岡女子学園中学校
三角形ABCをそのままにして、三角形ACDを図のように三角形AC’D’の位置に等積移動します。
すると与えられた条件から、三角形AC’Cは底角が15度の二等辺三角形になることが分かります。
後は、等しい辺の長さが10cm、底角が15度の二等辺三角形の面積が出せるかどうか?・・・基本事項!
頂角Aから底辺C'Cへ垂線を引き、その交点をHと置きます。次に、その直線でこの二等辺三角形を二つに分けます。そしてその二つの合同な三角形を、辺C'Hと辺CHが重なるように合わせると、頂角が30度の二等辺三角形になります。
この三角形は、上で説明した跡見の問題と同じです。
よって求める図形の面積は、10×5÷2=25㎠となります。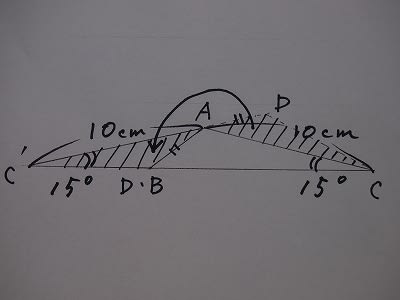
小学校の小学4年で学習する三角形の性質と三角定規について、学習を深めると今日の問題はその解き方が見えてきます。
二つの三角定規、30度・60度・90度の直角三角形は、正三角形を半分にして作られています。そのことが理解できていれば、一番長い辺と一番短い辺の長さの比が、2:1となることは容易に理解できるでしょう。
また、45度・45度・90度の直角二等辺三角形は、正方形を半分にして作ることができます。そのことから、斜辺の長さが出ているだけで、その三角形の面積を計算することができます。
この二つの三角形は、小学校だけではなく中学校や高校でも、三平方・三角比・三角関数の学習で出てきますので、しっかりと理解しておくことが大切です。
次回は、ちょっと工夫を必要とする平面図形の面積を求める問題で、入試に頻繁に出題される問題の求め方を伝授しましょう。

![]()
ブログ人気投票にクリックいただけると幸いです!
「一問必答」は、「一問一答」に掛けた造語として、今回のシリーズで用います。中学受験した学校に合格するために、ぜひ正解してほしい問題の中で、特に経験的に修得すべき基礎的知識を含む26年度の問題を取り上げ、ポイントを解説します。
今回は、前回に引き続いて二等辺三角形の性質を利用する問題です。ただ、ちょっと変形されているので、条件をよく整理して考えましょう。
【26年度の入試問題】 (分数の表記および記号が、実際の入試問題と若干異なります。)
今回取り上げる中学校は、女子美術大学付属中学校・頌栄女子学院中学校・鴎友学園女子中学校の3校です。いずれも26年度の入試問題です。
1.女子美術大学付属中学校
26年度の女子美の算数は、問題1が計算3題を含む小問10題、後は幾つかの小問を含む大問4題で構成されています。今回取り上げた問題は、問題1の小問の一つです。
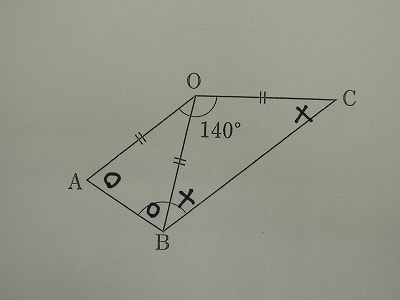
【問題】下の図で、OA=OB=OC、角AOCの大きさが140°のとき、角ABCの大きさを求めなさい。
2.頌栄女子学院中学校
頌栄の26年度入試問題は、問題1が計算問題を含む小問6題、その後大問4題の構成です。取り上げた問題は、問題1の小問の一つです。
【問題】下の図の三角形ABCはAB=ACの二等辺三角形です。xの角の大きさを求めなさい。
3.鴎友学園女子中学校
26年度の問題は、小問に近い問題が2題、問題3から問題7までは、小問2~3題で構成された大問5題でできていて、計算は出題されていません。そのうち今回の問題は、最初から2番目の問題です。
【問題】図のように、平行四辺形ABCDの対角線ACで三角形ABCを折り返してできる三角形を三角形AECとします。AB=ACのとき、角アの大きさを求めなさい。
このシリーズで取り上げる今春の中学入試問題は、私が作成した解説および解答を見ずに、まずは自力で解いてみることをお勧めします。大人には頭の体操になりますし、また受験生は、算数に対する興味や面白さが、倍増するはずです!
【解答と理解しておくべきポイント】
1.女子美術大学付属中学校の解答
2つの二等辺三角形が組み合わされた図形です。
この問題と同じように解く問題を、以下のブログで最近取り上げました。
マッキーの一問必答(8):慶應中等部の図形問題
三角形OABと三角形OBCの頂角の和が140度です。
下の図のように、等しい底角に印を付けます。
すると、求める角ABCは、2つの二等辺三角形の底角一つずつの和になっています。
2つの二等辺三角形の底角の和は、180×2-140=220
よって求める角ABCは、220÷2=110度
2.頌栄女子学院中学校の解答
この問題は、太線で示した四角形の角Bを求めることからスタートします。
これは一般的には、角Bの大きさが出ていて、130度の角を求めさせる問題として出題されます。
三角形の内角の和と、外角の定理を用いて角Bを出します。
公立小学校の5年生の算数指導を行ったとき、この角Bを求める方法をみんなに考えてもらいましたが、様々な解き方を考えてもらい、有意義な授業を行うことができました。
今日は、最も基本的な考え方を使って説明しますと、角130度と隣り合う内側にある角の大きさを、360-130=230度として求めます。
すると太線で示した四角形の3つの角の大きさが分かりますから、求める残りの角Bの大きさは、
360-(230+38+34)=58度と簡単に求めることができます。
三角形ABCは二等辺三角形でその底角の大きさが58度。
よって、その頂角BACの大きさは、180-58×2=64(度)
求める角Xは、64-38=26度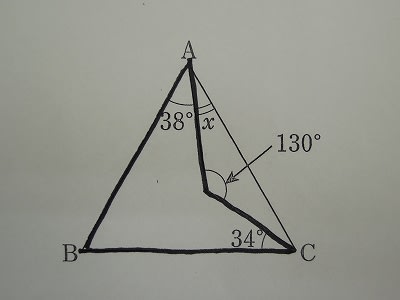
3.鴎友学園女子中学校の解答
下の図形で、折り重ねて重なった部分の三角形が二等辺三角形になっていることが分かるでしょうか。
角BACと角EACは折った同じ図形の頂角ですから等しいのは当然です。
また、角BACと角DCAは、平行線の錯角ですので、大きさは等しくなります。
このことより角EACと角DCAの大きさが等しくなリますので、角EAC=(180-88)÷2=46度
頂角46度の二等辺三角形の一つの底角の大きさは、角AEC=(180-46)÷2=67度
三角形の外角の定理(角AEC+角ア=88度)から求める角アは、88-67=21度
学校で小学4年に学習する二等辺三角形の性質を使う問題でしたが、その基本的な性質を入試問題で使えるためには、こうした問題を経験的に知識として習得する必要があります。
二回にわたって説明してきた二等辺三角形の問題は、その角度に注目して解く問題でもありました。次回は、特殊な角度に注目して解く問題について取り上げて解説しましょう。

















