ネイピア数eは名付けられないまま様々な形で現れていた。
1 自然対数の底として(底という言葉もオイラーが言い始めたという説がある)

2 ヤコブ・ベルヌーイの「連続複利の元利合計」として
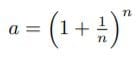
3 ヨハン・ベルヌーイの「対数が1となる数」として
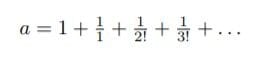
オイラーはeを抽出して名指しするのだが、それは指数関数の特別な形として現れた。
志賀浩二によれば、指数と対数の双対的な関係が明確になってきたのは1740年代だという。『無限解析』(1748年)の直前である。オイラーは
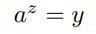 az=y ( z=logay )
az=y ( z=logay )
を基礎として、ここに微分係数
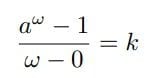
の関係を重ねてみたのではないだろうか。
微分の起点は0と1、これは加法と乗法の単位元である。指数関数を導く端緒として
a0=1
が設定され、微小な変位が導入される。
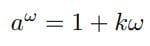
これに、まったく無造作に、代数操作(累乗)がなされ、次の式が導き出される。

ここに、改めて az=y が投影されて、指数関数が、

と表わされる。ここで、k=1、z=1のときa=eである。オイラー以前に指数関数はなかった。オイラーがはじめて冪から出発して指数関数を作り、eを指摘することになったのである。
1 自然対数の底として(底という言葉もオイラーが言い始めたという説がある)

2 ヤコブ・ベルヌーイの「連続複利の元利合計」として
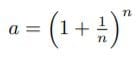
3 ヨハン・ベルヌーイの「対数が1となる数」として
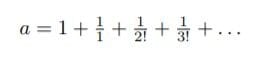
オイラーはeを抽出して名指しするのだが、それは指数関数の特別な形として現れた。
志賀浩二によれば、指数と対数の双対的な関係が明確になってきたのは1740年代だという。『無限解析』(1748年)の直前である。オイラーは
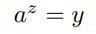 az=y ( z=logay )
az=y ( z=logay )を基礎として、ここに微分係数
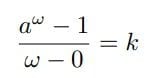
の関係を重ねてみたのではないだろうか。
微分の起点は0と1、これは加法と乗法の単位元である。指数関数を導く端緒として
a0=1
が設定され、微小な変位が導入される。
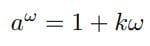
これに、まったく無造作に、代数操作(累乗)がなされ、次の式が導き出される。

ここに、改めて az=y が投影されて、指数関数が、

と表わされる。ここで、k=1、z=1のときa=eである。オイラー以前に指数関数はなかった。オイラーがはじめて冪から出発して指数関数を作り、eを指摘することになったのである。




















eの定義について書いた覚えがあります。
オイラーは対数の双対的な関係として指数関数を展望しました。冪から出発して指数関数を初めて作り、その逆関数として対数を捉えます。指数関数と対数関数の冪表示と級数表示を導いていく過程で、一般的な指数関数の特別な形としてeが発見され、見通しがよくなりました。
これは7章をなぞっているだけですが、オイラー自身のeの定義といってよいでしょう。このような定義は『無限解析入門』の解説としては見ますが、ネピア数eの解説としては見たことはないないように思います。
本文をもう少し展開してみたいと思います。