4元数の考察を始めたが、途中から「幻視のなかの橋」というイメージが出てきた。幻視のなかの橋2は、すでに書いていた記事(2つの原則、2元数と3元数、3元数の積)を前提にしていたので、「幻視のなかの橋」の2としては不十分なものになっているように思えた。幻視のなかの橋2を以下のように改訂する。
幻視のなかの橋2
2.1 i2=j2=-1
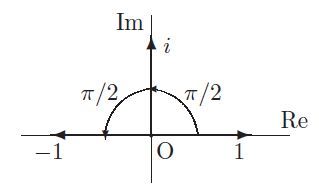
複素数の二つの元1とiは次のように表示される。元1を原点Oを中心にしてπ/2=90°回転した位置に元iがある。このiをπ/2=90°回転すると-1が得られる。複素数(2元数)a+biは実軸Re(x軸)、虚軸Im(y軸)の平面上の点(a,b)を表わす。
ハミルトンは複素数の二つの元1とiに対して垂直な第3の元jに気づいた。iがxy平面を回転するのに対して、jはxz平面を回転して-1になる。j2=-1である。j2=i2だが、jはiではない。3元数a+bi+cjは実軸Re(x軸)、虚軸Im(y軸)、虚軸I'm(z軸)の空間の点(a,b,c)と対応するのではないか。これがハミルトンの出発点だった。
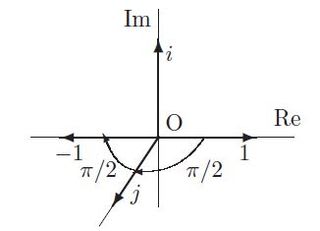
図は矢野忠「四元数の発見へ」(『数学・物理通信』1巻11号)より
2.2 2つの原則
ハミルトンが複素数から類推して3元数を構想したとき、端的にいえば、2つの原則があった。
1 体の原則 加減乗除について閉じていること
2 絶対値の原則 絶対値の乗積は、乗積の絶対値に等しいこと
|p||q|=|pq|
複素数で2つの原則を確認しておこう。
1 かけ算(だけ)で確認する。複素数同士のかけ算の結果は複素数になる。閉じている。
(a+bi)(x+yi)=(ax-by)+(ay+bx)i
2 |p|2|q|2 =|pq|2で確認する。
p=a+bi , q=x+yi,pq=(ax-by)+(ay+bx)i
(a2+b2)(x2+y2)=(ax-by) 2+(ay+bx) 2 成り立っている(ラグランジュの恒等式)。
2つの原則は複素数において成立している。
3元数a+bi+cjとx+yi+zjはどうだろうか。
注
(ax-by) 2+(ay+bx) 2
=a2x2-2abxy+b2y2+a2y2+2abxy+b2x2
=a2x2+b2y2+a2y2+b2x2
=a2(x2+y2)+b2(x2+y2)
=(a2+b2)(x2+y2)
2.3 ij=-ji=kの可能性
3元数a+bi+cjとx+yi+zjの積をみる。
(a+bi+cj)(x+yi+zj)
=(ax-by-cz)+(ay+bx)i+(az+cx)j+bzij+cyji
下線部の項によって3元数の積は3元数にはならない。ij=X+Yi+Zjと変形できるとも思えない。閉じていない。3元数は体の原則を満たしていないのである。
下線部を0とみなして、絶対値の原則と照らし合わせてみる。
(a2+b2+c2)(x2+y2+z2)=(ax-by-cz)2+(ay+bx) 2+(az+cx)2
この式は成り立っていない。左辺は右辺より(bz-cy)2だけ大きい。
すなわち、
(a2+b2+c2)(x2+y2+z2)=(ax-by-cz)2+(ay+bx) 2+(az+cx)2+(bz-cy)2
なら成り立つのである。
このbz-cyは下線部bzij+cyjiと密接に関係している。すなわち、ij=-jiと想定するとbzij+cyji=(bz-cy)ijである。
いま、3元1,i,jに加えて第4の元が見え隠れしている。ij=-ji=kとおこう。
2.4 k2=-1
i2=-1,j2=-1を基礎にk2の値を調べてみよう。
k2=(ij)2=ijij=-i(ij)j=-iijj=-i2j2=-1
i2=j2=k2=-1である。虚数単位として整合的ではないか。単独で図示すれば次のようである。
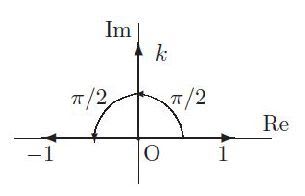
これは2元の図でiにkを重ねた図である。こちらは問題はない。
だが、1,i,jの関係と連立させて図示するとどのようになるのだろうか。

これは3元の図で1にkを重ねた図である。実軸は虚軸に隠れている。1とkは下の図では重なって見えるが、角度を変えて見ると上のように1とkは垂直である。
幻視のなかの橋2
2.1 i2=j2=-1
複素数の二つの元1とiは次のように表示される。元1を原点Oを中心にしてπ/2=90°回転した位置に元iがある。このiをπ/2=90°回転すると-1が得られる。複素数(2元数)a+biは実軸Re(x軸)、虚軸Im(y軸)の平面上の点(a,b)を表わす。

ハミルトンは複素数の二つの元1とiに対して垂直な第3の元jに気づいた。iがxy平面を回転するのに対して、jはxz平面を回転して-1になる。j2=-1である。j2=i2だが、jはiではない。3元数a+bi+cjは実軸Re(x軸)、虚軸Im(y軸)、虚軸I'm(z軸)の空間の点(a,b,c)と対応するのではないか。これがハミルトンの出発点だった。

図は矢野忠「四元数の発見へ」(『数学・物理通信』1巻11号)より
2.2 2つの原則
ハミルトンが複素数から類推して3元数を構想したとき、端的にいえば、2つの原則があった。
1 体の原則 加減乗除について閉じていること
2 絶対値の原則 絶対値の乗積は、乗積の絶対値に等しいこと
|p||q|=|pq|
複素数で2つの原則を確認しておこう。
1 かけ算(だけ)で確認する。複素数同士のかけ算の結果は複素数になる。閉じている。
(a+bi)(x+yi)=(ax-by)+(ay+bx)i
2 |p|2|q|2 =|pq|2で確認する。
p=a+bi , q=x+yi,pq=(ax-by)+(ay+bx)i
(a2+b2)(x2+y2)=(ax-by) 2+(ay+bx) 2 成り立っている(ラグランジュの恒等式)。
2つの原則は複素数において成立している。
3元数a+bi+cjとx+yi+zjはどうだろうか。
注
(ax-by) 2+(ay+bx) 2
=a2x2-2abxy+b2y2+a2y2+2abxy+b2x2
=a2x2+b2y2+a2y2+b2x2
=a2(x2+y2)+b2(x2+y2)
=(a2+b2)(x2+y2)
2.3 ij=-ji=kの可能性
3元数a+bi+cjとx+yi+zjの積をみる。
(a+bi+cj)(x+yi+zj)
=(ax-by-cz)+(ay+bx)i+(az+cx)j+bzij+cyji
下線部の項によって3元数の積は3元数にはならない。ij=X+Yi+Zjと変形できるとも思えない。閉じていない。3元数は体の原則を満たしていないのである。
下線部を0とみなして、絶対値の原則と照らし合わせてみる。
(a2+b2+c2)(x2+y2+z2)=(ax-by-cz)2+(ay+bx) 2+(az+cx)2
この式は成り立っていない。左辺は右辺より(bz-cy)2だけ大きい。
すなわち、
(a2+b2+c2)(x2+y2+z2)=(ax-by-cz)2+(ay+bx) 2+(az+cx)2+(bz-cy)2
なら成り立つのである。
このbz-cyは下線部bzij+cyjiと密接に関係している。すなわち、ij=-jiと想定するとbzij+cyji=(bz-cy)ijである。
いま、3元1,i,jに加えて第4の元が見え隠れしている。ij=-ji=kとおこう。
2.4 k2=-1
i2=-1,j2=-1を基礎にk2の値を調べてみよう。
k2=(ij)2=ijij=-i(ij)j=-iijj=-i2j2=-1
i2=j2=k2=-1である。虚数単位として整合的ではないか。単独で図示すれば次のようである。

これは2元の図でiにkを重ねた図である。こちらは問題はない。
だが、1,i,jの関係と連立させて図示するとどのようになるのだろうか。

これは3元の図で1にkを重ねた図である。実軸は虚軸に隠れている。1とkは下の図では重なって見えるが、角度を変えて見ると上のように1とkは垂直である。









