変動分布の裾(3) ──広義のt分布？──

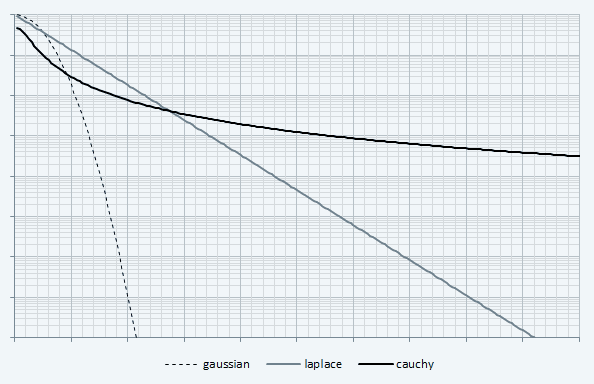
このシリーズで広義のt分布（以下tdwsと略す）と言ってるのは大雑把に言うと確率密度関数fが次のような形で、


（確率密度関数だから）全区間Rで積分すると1になる（超）関数のことである。


こういうのを一般に何と呼ぶのかは、たぶん本職の物理屋とか数学屋の人が知ってるはずである。わたしは本職ではないし、本職でなければ名前なんぞ本当はどうだっていいし（笑）、Google先生に訊いても要領を得ないし、今となっては身近に訊ける人もいない、というわけで単に直観的なわかりやすさからtdwsと呼んでおく。

通常のt分布（以下tdns）はベキのpが(1+k)/2である。正の整数kが自由度と呼ばれる。k=1のときがCauchy分布である。tdnsでは他のパラメータもk（と積分1の条件）に依存して定まるので、kは0以下にはならない（k→0でδ超関数になる）。つまりp=1/2以下ではtdnsは定義されない。手持ちのデータから読み取ってみる限りだと変動分布の裾はpが1/2未満なので（てことはCauchy分布よりさらに裾が厚いのである）、上式のようなtdwsを考える必要があるというわけである。

そんなエエカゲンなことでいいのかといって、今の場合t分布の統計学的な意味は本質的ではない。単に両側べき乗分布と呼べるものを作りたいだけである。むろんパラメータεの値によって、中心(x=0)付近の形が、したがって各種統計量も変わってしまうわけだが、変動分布の場合中心付近は、標本の大多数を占めるLaplace分布の標本で覆い隠されてしまうので、どっちみち概形はわからないし、わかったところで大勢に影響はない。肝心なのは裾の方がベキ乗で落ちてくれることで、中心付近はいい塩梅にぐにゃっててくれればいいのである（笑）──とはいえ最終的にはパラメタ・フィッティングが必要である。パラメータεの値によって標本全体に占めるtdwsの比率が変わってくるからである。

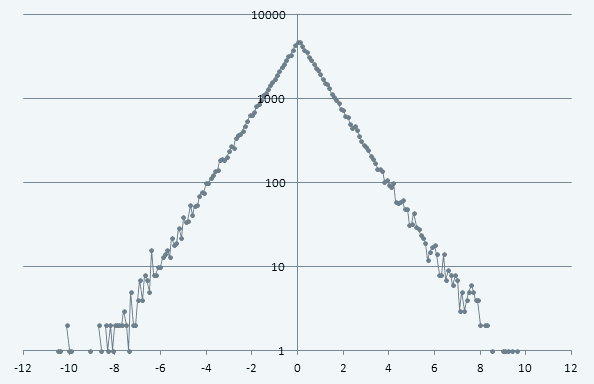
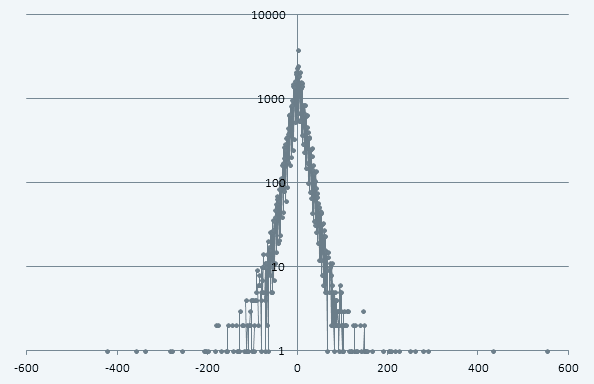
まあ何にせよ(2)の順位-変動グラフに、目分量で（笑）フィットさせたtdwsのサンプルを重ね合わせてみると、以下のようにバッチリ合う。tdwsでないとこうは合わないのである。


実を言うとこのグラフはtdwsの計算（正確に言うとtdwsにしたがう乱数の計算）がちょっと間違ってて、それで一番端の値がちょっと大きくなってしまっているのだが、概形としてはこの通りだし、グラフ作り直すのがめんどくさい（笑）ので、このまま出してしまう。

変動分布の裾(2)

外為相場の変動をヒストグラムにして描かせてみたことのある人というのが実際どのくらいいるものなのかは知らないが、WebでググってもLaplace分布とか両側指数分布という言葉はそんなにたくさんは見かけないので、どうせたくさんはいないのだろう（笑）。だから改めて掲げてみる。


薄い線が実際のデータから作ったヒストグラムで、細い線はこの分布がLaplace分布だと仮定した上でパラメタ推定し、求めたパラメタを使ってシミュレーションした、理論通りのLaplace分布のヒストグラムである。前回述べた通り、Laplace分布が線形に落ちるように見えるのは、縦軸を対数表示にしているからである。

こうして描かせてみると、分布の裾はどう見てもLaplace分布からは外れているわけである。この外れがあってもパラメタ推定にはほとんど影響しないのは、Laplace分布のパラメタ推定というのは要は「絶対値の平均」だから、分散の場合ほどにも外れ値が大きな影響を及ぼさないし、標本数の比率ではほんとにごくわずかな標本数でしかないからである。

それにしてもヒストグラムから目視で判定するというだけでは、ほんとに外れているかどうか確証できないではないか、というのはもっともな話である。実際、上のグラフでは頻度1の階級は表示もされないので、一番端の端がどうなっているかはわからないわけである。そこで、上の図の外れ値がほんとにLaplace分布から外れていることの証拠をお目にかける。


これはどういうグラフかというと、縦軸が変動(variation)、横軸は標本を変動の大きい順に並べた場合の、その順位である。ちなみに両軸とも対数表示である。この種の分布の裾の様子を調べるにはこれが一番である。Laplace分布のそれは順位が上がるにしたがって変動幅の増大も鈍ってくるのだが、実際のデータはまったく鈍らないでほぼ直線的に上昇していくことがわかる。

そしてこれが、変動分布の裾が「広義のt分布」にしたがっているということの動かぬ証拠である。

変動分布の裾(1)

この種の分布を考えるときに扱う3種類の代表的な分布、Gaussian分布とLaplace（両側指数）分布と、あとCauchy分布の概形を示してみる。まずは縦横とも線形スケールで表示させたもの。


次が縦軸だけを対数スケールにしたもの。こうするとLaplace分布が線形に落ちるようになる。縦横とも線形スケールだと3つの分布は区別がつきにくいのだが、これだとすぐにわかるわけである。


さらに両対数にするとCauchy分布が裾の方で線形に近づくことがわかる。これがいわゆる「べき乗分布」である。正負両側に裾のある分布がべき乗則に従うという場合、たいていはこのCauchy分布か、線形の傾きが異なる（広義の）t分布である。


いわゆる「ファットテイル」はGaussianより裾の厚い分布一般を指して言うので、Laplace分布もファットテイルのうちなのだが、本当に恐ろしいのはCauchy分布なのである。裾の方の頻度の落ち方がどんだけ違うかを、さらに先まで伸ばしてみたのが下のグラフである。


両対数にしたとき裾が線形で落ちるような分布は、大雑把に言って「どんな極端な事象でも起こり得ないということはありえない、これ以上は起こらないと想定していい限度がない」分布だと思っていい。実際、Cauchy分布というのは分散が存在しない。計算すると発散してしまうからである。

●追記
上で「（広義の）t分布」などと書いているのは、言い方を変えれば「両側パレート分布」ということになる。パレート分布はべき乗則の別名だが普通は地震規模の分布のような片側分布としていうわけである。こういうのは初等的な教科書には書いてないし、Webググっても案外要領を得ないので、時々勝手に造語してしまう（笑）

前回のおまけ

前回の図版でERLSのほかにふたつのメディアン系列が表示されているのは、そもそもあの図版は試行錯誤の途上で作っていたワークシート上のグラフだからである。

ボラティリティ推定を何に使うのかによって、その指標に求める特性も変わってくる。場合によっては立ち上がり／立ち下がりの反応の鋭さよりも、外れ値に影響されにくい平滑性の方が重要だという場合もある。その場合に最も効果的なのは中央値（メディアン）を使うことである。移動中央値系列は移動平均系列と同じように遅れを持つが、外れ値に影響されない特徴を持っている。特に分足の場合変動はラプラス分布か、それよりも裾の厚い分布になるわけで、外れ値の影響を受けない、少なくとも長く尾を引かないことは重要でありうる。

移動中央値を指数重みづけするとか、あるいは、いわゆる分位点回帰(quantile regression)を用いることで遅れを小さくすることはできるかもしれない（やってみたい人はどうぞ）。しかしこれらのアルゴリズムはERLSよりは（たぶん）複雑である。計算量は減らせたとしてもアルゴリズムやデータ構造の造作自体がかなり複雑である。異常値が入力された場合でもストラテジやプロセスを破壊しない程度に堅牢であるか（堅牢に作れるか）どうかというのは今後の課題である。

そもそも「指数重みづけ逐次分位点回帰(ERQR)」なんていうものをどうやって作ればいいのか、まだ調べてもいないのである（笑）。一般に信号処理という場合、外乱はAWGN（加法的白色Gaussian雑音）だと前提してかかるので、何かを推定しようという場合、その最尤性は何らかの意味で「最小二乗」法に属するものを用いればそれで済むのである。メディアンだの分位点回帰だのが必要になるのは、当の系列や外乱項が、どう見ても、近似的に考えても「Gaussian」の条件を満たさない、また満たさないことが本質的であると言っていいような場合である。

今回の場合「立ち上がりの反応性」ということを特に求めたので、むしろ外れ値に敏感に反応してくれる方がいいわけである。

●さらにおまけ

「平均値を取る」ことの意味が正確に理解されなければならない。それは単に足し合わせて割って文字通り均しているということではないのである。時刻と無関係な標本値集合{x}（標本数N）があって、標本のバラツキがGaussianである場合、その最尤推定つまり平均二乗誤差を最小化する値が「たまたま」平均値に一致するのである。Σ(x-m)^2を最小化するmはこの式をmで微分した式が0となる方程式

　　　　　Σ(-2x+2m)=0

の解である（もう面倒だし、単純な式だからTeX風図版は作らない）。これを解けばm=Σx/Nとなって、つまり標本値集合{x}の平均値そのものなのである。最小二乗法を用いるということは大なり小なり標本のバラツキがGaussianにしたがうということを暗黙の前提にすることだし、平均値を取るという操作も、暗黙に分布がGaussianであるという前提に立って初めて正当な意味を持つのである。

リーマン・ショックとかの直後には金融工学の悪口を言う人がやたらたくさん出てきて、その中には価格変動分布の「ファットテイル」をちゃんと考慮しないからだとか何だとかの捻った悪口もたくさんあったわけだが、それを完璧に考慮できているモデルなどがそうそうあるわけもないのである。だいたい、移動平均のクロスがどうした、ボリンジャー何たらがこうしたと、画面上を怪しいテクニカルチャートの意味不明な線と模様で一杯にしながら裁量取引をやってる人達は、その平均操作や（BBで使われている）標準偏差の数値的・統計的意味はほとんど不明であることを考えれば、少なくとも金融工学の算数に悪口を言う資格はないのである。

そうは言ってもまあ、先の「立ち上がりの鋭い逐次ボラティリティ推定」も、絶対変動の分布がGaussianから思いっきり外れることを利用して反応性を高めているわけだから、わたしもあんまり偉そうなことは言えない（笑）のである。

立ち上がりの鋭い逐次ボラティリティ推定法

ボラティリティの推定法はさまざまに考えられるが、この場合元系列が分足であるとして、1分間のレート変動の絶対値系列を「平滑化」したものを、ここでのボラティリティ推定と定義するとする。絶対変動系列をそのまま使えないのは、分単位で見た場合、数十pips以上動くことがあると思えば、その直後にはコンマ数pipsも動かないことが珍しくないほどバラツキが大きいからである。

問題はその「平滑化」として何を用いるかである、たとえば通常のMA（移動平均）の場合不可避的に遅れが生じる。一般にSMA（単純移動平均）よりはEMA（指数重みづけ移動平均）の方が、結果の滑らかさに対する遅れの度合いが小さくなるが、ボラティリティ推定の平滑化にこれらを用いた場合、特にボラティリティの急激な変動に対して反応が鈍いという点ではそれほど変わらないものである。

この立ち上がり／立ち下がりの反応を改善するひとつの方法は平滑化にEMAではなくERLS（指数重みづけ逐次最小二乗法）を用いることである。忘却率のパラメタ調整次第で相当に立ち上がりの鋭い、遅れの小さな推定が行えることがわかる。


例によって内緒にしておきたい事柄は全部表示から外してある。

ERLSと言って、早い話が各時刻において現在時刻を0と置いて（指数的に重みづけられた）回帰直線を求め、その切片を平滑値とするだけである。計算量はさほど増えない。オーダとしては（うまく作った場合の）SMAや（普通の）EMAと同じO(1)である。作り方は、最小二乗法や回帰分析の理屈を理解していれば誰でも作れるのだが、たいていの人はそんなもの覚えてもいないことだろうから、答だけ示しておこう。切片bの値は次の式で求まる。


ただしyが入力値の系列、rは忘却係数で1未満の値である。複雑そうに見えるかもしれないが、上の式にぞろぞろ並んでいる「シグマ（総計）」のほとんどは以下の式で求まる。


忘却係数rにしか依存しないので、rが組み込み定数ならこれらも予め計算して定数にしておけばいいわけである。分母は全体がひとつの定数になる。

定数化できないのはyを含む項で、これはyが更新されるたびに逐次的に更新しなければならないわけだが、実はその更新式も非常に単純である。


・・・要はこのTeX風の数式図版を見せびらかしたかっただけである（笑）。これが実はTeXではなく、もとはWordの数式フィールドを利用して作った（pdf出力してAcrobatに表示させてキャプチャして背景色調整）ものだと言ったら、たいていの人は驚くことになっている。

・・・って、今見たら最後のふたつのシグマの上の∞にマイナス符号をつけるのを忘れておったわ（笑）。図版作り直すのは面倒くさい（笑）し、更新式の方はこれで合ってるので、直さないことにしよう。

謎のヒストグラム

ほんとは謎でも何でもなくて、縦横軸の数字や目盛の表示を消してあるだけである。上は前から少しずつ作っているストラテジの、現時点での性能を示すヒストグラムなのである。分布の中心が縦軸よりちょっとだけ右にずれているわけだが、このずれた分が「エントリ毎の期待利益」に相当するわけである。具体的にどのくらいなんだ、というのはヒミツにしておきたいから数字も目盛も消してあるわけである。サンプル数も明かしたくないから縦軸の目盛や数字も消してあるわけだが、ヒストグラムのバラツキ具合からだいたいどのくらいなのか判断できる人はできてしまうかもしれない。

これだけだと、しかしさすがに寂しいのでもう少しサービスしてみる。


薄い線は同じストラテジを逆方向に適用した場合のヒストグラム、破線は対照実験として任意の時刻からエントリした場合のヒストグラムを、平滑化したものである。このストラテジが有効であることはこれでわかるわけである。念のため言えば、いまそこらの相対業者が提示しているくらいのスプレッドは楽々上回っている。このまま自動売買に組み込んでも利益は出るはずであるが、約定時のスリページとか、システムリスクとかは勘定に入ってないから、それも考慮すると、まだまだ安全なストラテジとは言えないのである。

●

微妙だなあ、と思う人もいるかもしれないが、このストラテジがベースになるわけである。根拠の怪しいアイデアや、検証しようにもサンプル数が足りな過ぎるとか、複雑すぎて統計的には確証できない「小技」のたぐいをこれの上に重ねて行くわけである。仮にそれらにまったく効果がなかったとしても、最低限このヒストグラムに現れている「中心からのズレ」の分だけは着実に稼げるわけなのである。

分布の裾の厚さを測る(3) ・・・シリーズ中断！

無知というのは怖いものだ。

改めて丁寧に調べてみたら、このシリーズで考えようとしていた問題というのは極値理論(EVT; Extreme Value Theory)といって、数理統計学の分野では1920年代とか、だいたいそのくらいから熱心に研究されてきた問題の、ほんのごく一端にかかる事柄にすぎないことがわかってきた。このシリーズで扱う予定だったアイデアというのも、キーワードとして「順位統計量(order statistics)」とか、「分位関数(quantile function)」とか、だいたいそのあたりから攻めて行くと、ひと通りの理論から応用まで、だいたいのところは尽くされてしまうようである。

もちろんEVTはファイナンスの分野でも大いに注目され参照され応用されている、ように思える（酔っ払った頭で調べてみた限りでも）。わたしが知らなかったのは、単にわたしがこの分野についてど素人で無知だから、というだけのことだったようである。

というわけでこのシリーズはいったん中断する。中断するけれども、何にせよこれまで全然知らなかった話であることは確かだし、とても面白そうな理論なので、少し手間をかけて調べてベンキョーしてみようと思う。で、その成果があったら、それを踏まえてシリーズを再開することにする。別に言い訳するつもりはないが、普通にはそれほど知られていない理論であるように思えるし、上のタームで検索しても和書ではそれらしい本が見当たらないことは確かである。「分布の裾の厚さ」とか、そういう語彙で検索してもそれらしいものが見当たらなかったのも本当である。

分布の裾の厚さを測る(2)

(1)の最後の方に述べたことを図解してみる。ラプラス分布（両側指数分布）というのは下図のような概形の分布である。


ただの三角やんけ、ではない。縦軸は対数表示であることに注意。

そして以下が実際のドル円レートの分あたり変動の分布である。

まさしくラプラス分布であるように見える、が、よく見ると裾の方が広がっている（裾が厚くなっている）ような気がする。気がするが、はっきりわからない。上のグラフでおおよそ±150（×0.1pip)より外はすべて出現回数が1回なのである。正の側を拡大してみたのが以下の図である。


ヒストグラムの階級幅をある程度大きくすることで多少は伸ばせるが、階級幅を大きくしすぎると概形が掴みにくくなってしまう。特に±200を超えた先の領域はもう、本当はどんな分布なのだか、このヒストグラムだけからは一切わからないと言っていい。それを調べてみよう、というか調べるための（多少とも合理的な）手法を考えてみよう、というのがこのキカクである。

分布の裾の厚さを測る(1)

今朝方、ゆうべ色々やるつもりで調べていたのに「全然ダメだった」と書いたのはこれである。ひとつアイデアを思いついて、それが随分単純なアイデアだったから、こんなのは前例がいくらでもあるんだろうと思ってWebを調べたのに一向に出て来ないわけである。思いつきのアイデアとしては悪くもなさそうだし、実用性もありそうなのだが、理論的にはっきりしないところが多いので、そこらへんのフォローが得られればいいなと思ったのだがそれがない。

仕方がないから、とりあえず理論もへちまもないままでアイデアの現状を書いてしまう。

株価や外為レートの（対数）変動分布は正規分布にならない、ということは、今ではよく知られていることだと思う。だいたいは正規分布よりも「裾が厚い」、いわゆる「ファットテイル」と形容されるような分布で、そういう分布は正規分布を仮定した場合にはありえないような大きな変動が、ありえない大きな確率で生じるわけである。

金融工学における相場のモデルや投資・投機戦略というのは、少なくとも理論の最も基礎的な部分でたいがい正規分布を仮定している（なんと言っても数理的に扱いやすいからである）。そのままでは実用的でないから、現実的なモデルや戦略はいろいろの修正や補正を加えた上で使われているわけだが、そうは言っても複雑なモデルのあちこちに正規分布がからんでいるし、理論的なパーツの全部をスクラッチから作っている人も組織もめったにないわけで、まあ、あちこち放ったらかしになっているわけである。

むろんわたしは金融屋ではないし、実際に賭けたことはないという意味では投資家ですらないから、別に見たわけではない。実際はどうだか知らない。ただ、サブプライムなんたらとかリーマン・ショックのような大事件が起きると、最近ではたいていその種のモデルの不備が絡んでいると言われていて、それが本当なら、ショックは事実として起きているわけだから、上はたぶん妥当な背景事情の説明だということになるはずである。

こうした話は金融や投機に絡んであるばかりではない。福島の原子力発電所の事故にしても、根本的には、起こるであろう地震や津波の規模と頻度についての「読み（想定）が甘かった」ためにあのような大事故になってしまったと言われている。地震や津波は相場の変動とよく似た「べき乗則」の分布を持つことが知られていて、それは最近では割合よく知られていることであるにもかかわらず、それが安全対策に十分反映されていなかった（ように思える）というのは、その理由のひとつとしては、分布の概形はわかっても本当の裾の厚みはよくわからないからではないかという気が、わたしはしているわけである。

「本当の裾の厚みはよくわからない」ということに意外な落とし穴がひそんでいるのは、外為相場の変動分布が典型的である。その分布は概形としてはラプラス分布（両側指数分布）を描くことは、そこらのヒストリカルデータをもってきてExcelでグラフを描かせてみれば誰にだって、小学生でもすぐわかるわけである。真の現実的な危険はその先にある。つまりその分布のグラフでは隠れてしまっているような、分布のほとんど一番外側では、実はラプラス分布よりさらに「裾が厚く」なっているのである。

ここまでは、しかし、ちょっと本格的な相場分析の専門書などには結構書いてあることである。ただ、そうした本でも、じゃあ実際のところ、正味の「裾の厚さ」はいかばかりなのかということになると、それほど明確なことは書かれていない。分布の最も外側というのはそもそも百万サンプルに1回生じるか生じないかのような、普通だったら「例外」とか、統計では「外れ値」などと呼ばれてしまうような領域で、もともと十分な理論解析はできっこないような領域なわけである。

だからと言って放っておくわけには行かないわけである。理論的に説明可能であろうとなかろうと現実の相場の変動は現実の利益や損失に直結するわけである。理論的に説明できないからさっきのオーダーはキャンセルだ、などという後出しジャンケンは通用しないのである。それが通用するくらいなら金融ショックも原子力発電所の事故も、この世には恐るべき何事もないということになるだろう。残念だがそうは行かない。

前置きが異様に長くなってしまったのでここらでいっぺんうｐする。

（つづく）

ボラティリティ変動の自己相関（追補）

前回、自己相関関数に対数近似曲線がフィットするのは、元データを対数変動でなくただの差分で取ってしまったからだろうと書いたが、それは勘違いだった。改めて対数変動でやってみても結果の自己相関の概形にほとんど変わりはないのである。

勘違いの罪滅ぼしに、というわけでもないのだが、発掘したデータを元にして追加のグラフを取ってみた。前回の自己相関関数が、1440分でピークを持つことを筆頭に、数値的にはかなり暴れているのは、日内変動を考慮していないためではないかと思って、それを除去した上で改めて自己相関を取ってみたのが以下である。ちなみにこのグラフの元データは対数変動である。


日内変動を除去すると最初の百分以降はほぼ無相関になることがわかる。逆に言えば日内変動を除去しても最初の百分の自己相関は消えないのである。拡大したのが以下である。


厳密に言うとごく薄い相関が実に300分近くまで裾を持っているらしいことが見て取れる、けれどもこれは日内変動を除去する処理の副作用として生じたものかもしれない。ここでは特に原因は推測しないでおく。

最初の百分、厳密には70~80分の期間が対数近似にフィットすることをよりはっきり示すのが次のグラフである。


誰がどう見たって対数なのである。

で、この対数近似が一番よくフィットしてしまう理由だが、厳密なところはわからない。あくまで推測だが、この曲線はレート変動のラプラス分布（両側指数分布）を反映しているのかもしれない。つまり大きなレート変動は地震のようなもので、規模の大きなイベントほど前後に長く「余震」を伴うと考えれば、変動規模の分布がボラティリティ変動の自己相関に反映されるということはありうるように思える。

ボラティリティ変動の自己相関

手元には外付HDDが実はいくつもあって、復旧作業のために古いバックアップファイルを調べていたら、ちょっと懐かしいものを見つけたので画像として貼ってみる。


題名すら入ってないのであれだが、これはつまりドル円レートの分あたり変動の自己相関を取ってみたグラフである。変動そのもの（淡色）に自己相関はないのだが、絶対値を取った瞬時ボラティリティ（黒）には、値としては小さいが自己相関が明瞭に存在するわけである。そう説明しなくてもグラフを見ただけで判る人がいるかもしれないくらいに有名な事実だが、それを実際のデータで検証してみたというものである。なんでグラフを見ただけで判るかと言えば、1440（分）のところにひとつのピークがあるからである。1440分とはつまり24時間のことである。

もうひとつ、250分の範囲で拡大して近似曲線を重ねてみたグラフもあった。


線形や多項式ではなく対数カーブにフィットするのは、もとの計算で対数変動ではなく差分の絶対値を取ったからであると思われる。普通は対数変動を用いるのだが、あえてそうしなかったのは、その方が明瞭な自己相関が得られるかもしれないと思ったのかもしれない。何にせよ大雑把に見ても150分、見方によっては200分も相関が尾を引いているのがわかる。

rationality in decision (3) ─スキャルピングの困難─

スキャルピング(scalping)とは「皮剥き」というほどの意味で、短時間のうちに決済することを繰り返し、薄皮を剥ぐようにちまちまとゲインを稼いで行く手法のことである。ややこしいのは、この「短時間」というのが人によって異なった意味で使われているということだ。数時間でも1日あたりの決済回数がコンスタントに複数回であるような手法は、つまり文字通りの「デイ・トレード」以上の頻度で取引を行うものはみんなスキャルピングに含めてしまう人もいれば、秒単位（たかだか数分以内）で決済するのでなければスキャルピングではない、というような意見もあったりする。つまり前者は取引の頻度について言っているし、後者はエントリからイグジットまでのホールド時間の長さの規模について言っているわけである。さしあたりここでは後者の意味でいうことにする。

時間の規模はともかく、できるだけ短時間で決済したいという考えがどこから生じてくるかといえば、未来のレートの予測は、時間が短ければ短いほど確率が高くなるという見方から生じている。最初に言っておくと、これはおおよそ事実である。むろん現実の取引にはスプレッドがあるわけで、高頻度の取引はスプレッド分だけでかなりのロスになるのだが、予測の確実さにはかえがたいということであるのだろうか。

それにしても数分以内に決済してしまうのは、統計的に見ればまず勝ち目のない手法である。そもそも短時間であれば未来のレートの予測確率が向上するといって、そんなに大きく向上するわけではないのである。55%が56%になるとか57%になるとか、せいぜいそんなものでしかないのである。まあそれでも向上することはする。しかし一方で、1分間でどのくらいレートが動くのかを考える必要がある。比較的近年の円ドルレートの推移でみると、分あたり変動の絶対値の中央値は大雑把に言って1pip内外である。そして円ドルのスプレッドは大雑把に1pip前後だから、スプレッド分を稼げるか稼げないかである。予測の的中確率がたかだか60%にも満たないところでそのような取引を繰り返せばどうなるか。シミュレーションしてみるまでもなく勝ち目はないと言っていいわけである。

にもかかわらず分刻みとか秒刻みとかのスキャルピング手法にこだわる人がなぜ（そんなに少なくはない数で）いるかというと、変動幅の中央値ではなく平均値で、あるいは標準偏差でみると値がもっと大きくなるからではないかと思われる。ほんの1分の間に10pips、時にはどかんと50pips以上も動くことがあって、これを的中させれば、かつ高レバレジであれば、確かにものすごいゲインになるわけである。

もちろん逆の場合もあるわけだが、そこは「目押し」の能力で、どかんとロスする前に決済してしまえばいいだろうと、だいたい安易にそう考えられていたりするように思える。それほど大きく動く時はスプレッドも拡大するし、取引量が急増して「市場の（ある意味で時間の）流れが速く」なっている、その分だけスリページも大きくなる道理だということは、どうしてか都合よく忘却されている（スリページは全部業者のインチキだと思ってる人もいるが、それは間違いだ。業者にインチキがあるとすれば、ボラティリティが増大している時間帯は自然にスリページが大きくなるのを言わないで、標準的な時間帯のスプレッドの狭さや、あるいは「固定スプレッド」を強調して宣伝することの方にあるというべきである）。ボラティリティの増大は必ずしも期待ゲインの増大には結びつかないのである。

1分で50pipsも動くのは月に1度あるかないかである。一度これに勝てばしばらくはリッチな気分に浸れるし、たまたま2度3度続けて勝てば非常にリッチになれる。けれども逆のことが起きれば一転して文無しである。いったんは大金を手中にしても、その後「1年と経たないうちにひと財産失って退場してしまう」という、外為投機でよくあるシナリオは、だいたいそんな風に反復されているのだろうと思われる。本当のところは爆益と爆損の時だけ「時間がものすごく早回しになっている」だけなのだと思うべきである。

わたしの現在までの分析では、比較的高い予測確率を保てるのは大雑把にエントリからxx分（この値はヒミツにしておこう）程度までである。それより長くなると何をどうしても実効的な予測の的中確率は悪くなる。実効的な、というのは、数値的にはむしろ平均ホールド時間が長くなるほど的中確率は非常に向上するように見えるのである。だがこれは以前述べたような「組み合わせパタン数の拡大」と「一致頻度の減少」が生み出す錯覚、よく言われるところの「カーブフィッティング」にすぎない。非常に重要な結論はこうだ。平均ホールド時間を短くすればするほど実効的な予測の的中確率は（わずかだが）単調に増大する。一方で取引あたりの（スリページやら何やらを含めた）実効スプレッドロスも単調に増大する。したがって両者がバランスするところに最適解が存在し、かつ一意に定まる、ということである。

存在するかもしれない、ではない。繰り返すが、最適平均ホールド時間は「存在して一意に定まる」のである。これが合理性である。

以上の結果を導くのにむつかしい算数はいらないし、バカみたいに高価な（しかも、そうしたものに限って、たいていはひどく使いづらい）専用の分析ツールもいらない。Excelと理性があれば誰でも──理性の方は誰にでも公平に配分されているとデカルト先生が言っている──できることなのだ、ということを強調しておきたい。

（つづくかどうか）

rationality in decision (2)

さり気なく新規にカテゴリを立てて始めてしまったわけだが、実のところこの企てにはほんの少しばかり真面目な目的がある。真面目な目的というのはつまり、それが達成可能なことかどうかは二の次だということである（笑）。

それは何かというと、わたしは外為証拠金取引の現在を憂えているのである。つべこべ言っても業者は客をハメ込むことしか考えていないように見えるし、客は客でパチンコやパチスロよりもわけの悪い素人ギャンブルの意識しか持っていないように見える。業者も客もそんななら監督官庁たる金融庁もそれ以上のものではありえなくて、これを一種のハイリスクな宝くじか何かのように思いなして、あんまりひどいことが起こらないように規制をかけるとか、だいたいそんな方向にしか発想が向かっていないわけである。この悪弊は三方のそれぞれにおいて、また全体の構図としても改められてしかるべきだというのが、その「真面目な目的」である。

これが真面目な目的である限り、そんなことは現実にはなりっこない、ほとんど無意味な空想的願望にすぎないわけである。ただでさえいまわが国はふたたび世界の最貧国へとまっしぐらに転落しつつある、わけである。この期に及んで素人の小銭稼ぎだけがどうしてか世界が刮目するほど立派なものになるなどということは、普通に考えてありそうもないことである。

---

先週出だしだけ書いてほったらかしになっていた「エントリ／イグジットにおける合理性」の続きを少し。

いつものことで詳しくは書かないが、わたしの分析結果によれば、エントリ／イグジットの条件が合理的でありうるとすれば、特にイグジット条件をレートではなく時間志向にすることである。つまり、ある時刻t₀にエントリしたら、イグジットは必ずそのN分後のt₁=t₀+Nに行うこと、これを他のあらゆる判断条件の根本に据えることである。

本当かよ、と思うかもしれない。当たり前の話だが上のイグジット条件だけで勝てるわけではない。そうではなくて絶対確実な戦略というものを考えた場合、それはどんな場合でも上のイグジット条件を含むはずだということである。

絶対確実な戦略って何だと思うかもしれないが、別にどうってことはない。上の条件に加えてストップロス条件を0にする（限りなく0に近付ける）ことである。エントリ方向からみて損する方向に入ったらその瞬間にロスカットするわけである。何のことはない、マルチンゲールの逆である。ただタイムリミットNを有限に設定することだけが違う。なんで有限の時間で切るのかと言って、Nが無限大であれば1次元ランダムウォークは有限時間内に100%原点に回帰することが数学的に証明されているからである。つまりNが無限大のときこの戦略はゲインもロスもないイーブンな戦略である。一方、Nが有限のときはゲインだけがあってロスがない、つまり絶対に負けないわけである。

もちろん、以上は現実には不可能な戦略である。現実にはスプレッドやスリページがあるし、そもそもストップロスをエントリ相対で0に置くことはできないわけである。スプレッド、スリページ、ストップロス値幅制限が0でない場合、大なり小なりロスする可能性があるわけで、したがって現実的な戦略は絶対ではありえない。現実にゲインできる戦略とは、だから、このマイナスを帳消しにしてそれを上回る程度には「五分五分よりは大きな確率でレートの騰落を予測する」手法の存在と不可分である。

どんな手法を駆使してもこの場合の予測は5割をそんなに大きく上回るものではありえない。5割5分、奇跡のようにうまく行って6割である。前者はほとんどの現実的なマイナス条件を覆すにたりない。また後者は決して長続きしない。

（つづく）

自動売買のリスク列伝

自動売買の安全対策が実際にどんなに煩わしいもので、しかも完璧を期し難いものであるか、以前に自分で考えていた時のことを思い出して列挙してみる。

　　・PCとHDDは突然お亡くなりになる
　　・クライアント・プロセスは突然異常終了する
　　・クライアント・プロセスは黙って正常終了する
　　・ウィルススキャンは相場の空気を読まずに開始される
　　・指標時には突然自動バックアップが開始される
　　・俺はデフラグなんて設定した覚えはない
　　・チャートもEAもさっきまでは確かに動いていたんだ！
　　・電源ケーブルのプラグは予告なしに抜ける
　　・計画停電は中止になった？ああ、ありゃう（断
　　・電力会社は政治判断で原子炉の停止を命じられる
　　・ネットワーク・ケーブルのプラグは予告なしに抜ける
　　・慌てて再挿入しようとしたらプラグのツメが折れる
　　・ケーブルの予備などあったためしがない
　　・珍しくあったと思ったら断線している
　　・慌てて買ってきたものはクロスケーブルである
　　・ルータはとりあえず落ちる
　　・人が監視していないVPSは落ちる
　　・人が監視していないVPSの監視モニタは落ちる
　　・人が監視していない監視モニタの監視モニタは落ちる
　　・分散されたリスクは数年後のある日思いがけない再会を果たす
　　・DNSは相手先のことを知らないという
　　・pingは迷子になったまま帰って来ない
　　・ネットワーク・プロバイダは無期限で休業する
　　・大地震（だいじしん）は必ず起きる
　　・大津波はわが家のすぐそこまで迫っている
　　・業者とサービスはある日忽然と姿をくらます
　　・業者はすべてを強制LCしてから帰ってくる
　　・業者がすることはすべて取引所も真似をする
　　・取引所がすることはすべて所轄官庁も真似をする
　　・世界は滅亡する
　　・だが、追証は滅びてはいなかった！

・・・読んで笑える範囲に限って書き出してみてもこんなものである。本当はこの何倍かの「常時考慮しなければならない緊急事態」が存在する。自動売買と言いながら、やってる人はプログラムが動いている間はもう一睡もできやしないというのは、よく見かける話である。

「安全な取引環境」がいかに高価であるか

外為取引の自動売買をMetaTraderとかのツールを使って（それなりに本気で）やろうという場合、大雑把にどのくらいのことを考えに入れなければならないか、今日探してみた限りだが、国内では現時点でこれひとつだけではないかと思う、真面目に考察しているblog記事を見つけた。

　　システムトレードの災害・障害対策について ─ FXシステムトレード初心者奮闘記

わたしが今までどうして相場分析ばかりで実際にEAのコードを書いたことはほとんどない（MQLのベンキョーのために少しは書いているけど）のか、自分のやってることがほんのお遊びにすぎないことだと言い切れるか、その理由は上のページを読めばとてもよくわかると思う。自動売買ということを本気で真面目に考えるとしたら、普通に考えてもまずこの程度は最低限考慮に入れなければならないわけである。「『FX自動売買』とか、なんかそういう名前のついたプログラムを買ってきてPCにインストールすりゃいいだけだろ」なんていうのは、言葉のあらゆる意味で単なる自殺行為にほかならないのである。

で、自分でも以前にすこし考えてみたことがあるから言うわけだが、それにしたって、まあ、ここまで考えるだけでも死ぬほど面倒くさい（笑）わけなのである。さらに、上で書かれているような指針に沿ってコードを書いたりシステムを構築したり、さらにデバッグとテストを繰り返して実稼働までこぎつけるのは、本当に気が遠くなるような時間と労力を必要とするはずのことである。仮に全部をSEの人件費に換算したら、その年収くらいは軽く吹っ飛ぶくらいのことである。そしてそれだけやっても、そのシステムが実際に利益を生み出すのかどうかといったら、そこにはほとんど何の保証もないのである。このblog主はめげずにそれを自力で、単独で、本当に（笑）やろうとしているわけである。掛け値なしに偉いなと思う。

なんだこのくらい、ソフト屋なら誰だって当然考えることじゃないかと言えば言えるのだが、たとえば上のページの中で「携帯から一発で、全保有ポジションを手放す指示をMT4(MetaTrader 4)に送れたらいいなぁ。」と書いてあるところなどは、本当にそうだとわたしも思うわけである。この主も書いているように、事実としてこうした緊急時対策をサポートしている業者はなぜかどこにもないわけである。携帯電話やモバイル機器による注文に対応することは、割とどこでもやっているし、自動売買に対応している業者も（国内だと数は少ないが）ある、しかしそうした業者でもこういう安全対策には、なぜかまったく関心がないかのようなのである。業者にないのだから金融庁とかにはもっとないわけである。

●（追記）
上を書いた後で調べ直してみたところ、MetaTraderでなくてよければ、自動売買を行う一方、「携帯電話から一括決済」を受け付けるサービスは存在するようである。具体的にどこかはググって調べていただきたい。また、接続ポートではなく根元のサーバが落ちているような場合は、PC経由だろうと携帯電話経由だろうと口座にアクセスすることはできず、未決済のポジションが宙吊りにされてしまうことに変わりはない。