二十四節で、3 月 6 日は「啓蟄(けいちつ)」。冬ごもりから目覚めた虫が、顔を出す頃。
そして3月7日は満月。アメリカでは「ワームムーン」と呼ばれているとか。

さて、子どもたちに月の話をしていると、月までの距離は38万キロというのは、図鑑大好き小学生はよくしっています。
物差しで測れない月までの距離はどうして測ったのだろうと質問すると「?、、、」
今回は月までの距離の求め方から
月までの距離
現在ではレ-ダ-の電波を月面に当て、電波が往復にかかった時間を調べて距離を求めます。それによると
地球に最も接近した時…… 35.6万km
〃 離れた時 …… 40.7万km
地球~月の平均距離 …… 38.4万km となっています。
レーダーの発達する以前は、下図のようにして求めていました。
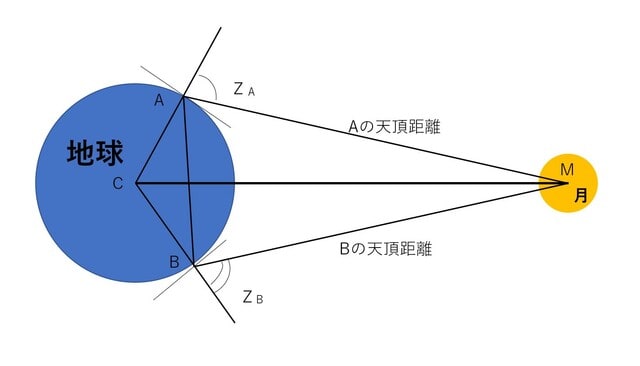
AとBは、同一経度線上にあります。
両地点で同時刻に、月の天頂距離、即ち
∠ZAM、∠ZBM、(Z;天頂) を測定します。
すると、図から
∠MAB = 180°- (∠ZAM +∠CAB)
∠MBA = 180°- (∠ZBM +∠CBA)
A、B、両地点の緯度は分かっていますから、AB間の直線距離ABと∠CABおよび∠CBA はすぐに求められます。従って、三角形MABにおいて、ABと∠MAB、および、∠MBA、(2角と1辺) が求まったので、AM、および、BMが求められます。
月は平均38万4千kmの遠くにありますが、光なら約2.56秒で往復します。アポロでの月旅行では何日かかったでしょうか。
つづいて月の大きさももてめてみましょう。
月までの距離が分かると、月の大きさ(直径)を求めることができます。
それは、下図のように月の視直径を測定して計算します。
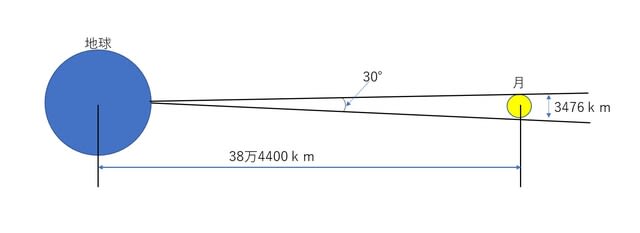
月の距離は、およそ36万km~41万kmに変化するので、視直径も29′から33′まで変化しますが、今、その視直径を30′、距離を384,000 kmし、月の直径を半径384,00kmの円弧の一部と考えて
360 ゜ : 30′ = 2 π×384,000 : X
故に X=(30′/360)×2 π×384,000=3,352km となります。
これは、地球の直径(12740km) の約 1/4 になります。
でも、古代ギリシャ人はおおよその距離や大きさは計算していました。
地球の大きさをもとめ、月食から月の大きさや距離を計算してたようです。
むつかしい話はここまでにして 今日は十六夜の月、たのしみましょう。











