望目特性SN比の再現性確認についての考察

 18直交表を使ったパラメータ設計では、８個の制御因子（システムの構成要素）に２～３個の水準（構成要素の選択肢）を割りつけ、少なくとも２水準のノイズ因子環境下で１８組の実験ごとに２つ（以上）の実験結果を得る必要があります。

　つぎに、１８組の実験ごとに得られた２つの実験結果の『平均；m』と『分散；V』を１８対計算します。

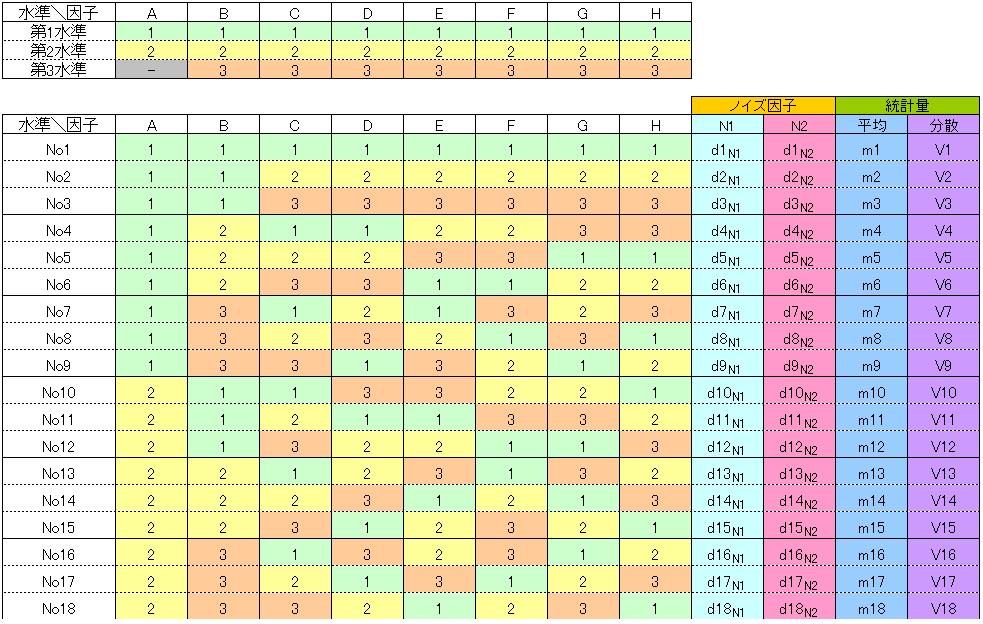
　つづけて、18組の実験ごとに、『平均』の2乗を真値とする『感度』と、『感度』の真値を『分散』で割った結果を真値とする『望目特性のSN比』を計算します。

　そして、各制御因子の水準ごとの『要因効果』を計算します。『要因効果』とは、その制御因子・水準がシステムの出力結果におよぼす影響の大きさです。『感度』と『SN比』両者の『要因効果』を計算します。L18直交表の場合、『感度』と『SN比』それぞれ、２＋３×７＝23個ずつの『要因効果』を計算します。

　ある制御因子、ある水準の『要因効果』は、その制御因子、その水準が関与した実験を抽出して総和し、データ数で割る、つまり、平均を計算して求めます。たとえば、制御因子Bの第2水準に関する『感度』の要因効果は、実験No．４～６とNo．13～15の『平均』を２乗して総和し、６で割った値です。このような計算で『要因効果』が求まる理由は、システムの出力は、各制御因子の出力に関する影響の足し算で成りたっている、つまり、『要因効果』の加法性が成立しているという前提があるためです。

　『要因効果』の加法性が成立するためには、各制御因子が独立している、つまり、制御因子間に交互作用がないことが必要条件です。

　制御因子が独立していて、システムの出力がその効果の加法性で成立しているとき、18組の各実験結果は、各制御因子の水準の『要因効果』を足し合わせた結果になります。（実際はその値から全体平均の７倍を引いた値ですが。）

　『感度』のもととなる実験結果の『平均』；mは加法性が成りたつため、『感度』の真値を常用対数変換した実用上の『感度』も加法性が成立します。

　一方、制御因子が独立している場合、統計学上、『分散』；Vも加法性が成りたちます。

　しかし、『SN比』の真値；ηは、η＝m＾2 / V で計算しますが、このとき、分数の分母は加法性が成立しません。　

1 / 2＋1 / 3 ＝2 / 5 ではないのです。

　つまり、『感度』の場合、18組の『平均』 から制御因子・水準ごとに『平均』の要因効果を計算して、そのあと、『平均』の『要因効果』を２乗して『感度』の真値をもとめ、常用対数変換した結果である『感度』には加法性が成立するのですが、18組の『SN比』から計算した各制御因子・水準の『SN比』の『要因効果』には加法性が成立しないことになります。

　実務上実施したパラメータ設計では、『感度』は再現しやすいけれども『SN比』は再現しにくいという経験が多い気がしています。また、私の所属している地方研究会での報告でもその傾向が強いように感じていました。

　これは、18個の『SN比』から計算した制御因子・水準の『SN比』の要因効果には加法性がない、ということが原因ではないかと考えています。

　パラメータ設計では、実験と結果の解析を行なった後、『最適条件』と『対抗条件』の２つの確認実験を行い、『感度』と『SN比』の再現性をチェックして

1．実験が成功したといえるのか？

2．得られた結果を信頼してよいか？

の判断をすることになっています。

 　しかし、今回の内容のように、もともと一般的な品質工学流のやり方で計算した『SN比』には加法性が成立しないので、『SN比』の再現性が低かったとしてもそれほどがっかりすることはないと思います。『感度』の再現性が高ければ、実験は成功していて、得られた結果を信頼してもよい、ということでよいと思います。

　では、どのように『望目特性のSN比』を計算したらよいか、ですが、現在まだよい方法が見つかっていません。ただし、新たな計算方法を見つける旅の入り口には立ったかな？と思っています。

その入り口について、次回報告します。