完全互換の方法による公差解析は意味がない！（一様分布の特性）

　かなり過激なタイトルにおどろかれた方もいることでしょう。
　昨日、先月開催されました日刊工業新聞社様主催のMT法に関するセミナーを
受講された方からのご質問を受けました。そのご質問は、一様分布するような
事象を項目に含む対象に、MT法は使えるか？というものでした。

　私は、MTシステム、公差解析、分散分析、実験計画法、品質工学、信号処理
などのセミナー講師をさせていただいております。

 どれも、統計学の知識が不可欠で、セミナー対象と同じくらい、統計学の解説に
力をいれています。これをしないと、セミナー対象の本質を理解していただけない

からです。

 統計学の解説のなかの中心極限定理の説明では、下の図を使います。
 中心極限定理とは、もとの分布がどのようなものであっても、そこからｎ個の
サンプルを取りだしてその平均を計算する、そして、これを多数回くり返すと
得られた多数の平均の群れの平均は、母平均にちかづき、群れの分散は、
母分散の1/ｎにちかづく。そして、さらに、その群れは正規分布にしたがう。
というものです。

さて、下の図をご覧ください。

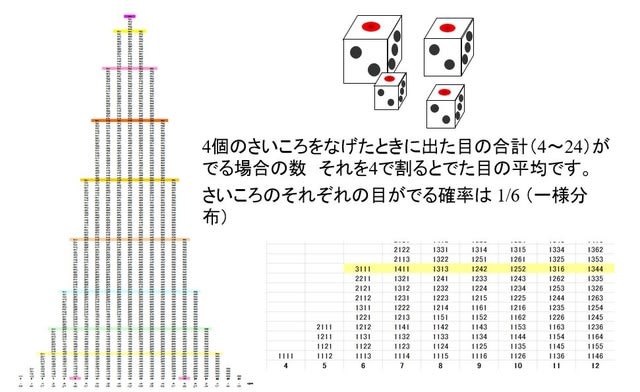
　さいころの出る目はすべて1/6です。つまり、確率密度は一様分布になります。
　大きさちがいの４個のさいころをなげて、その出た目を合計すると、4×1＝4
　から、4×6＝24、（4～24）になります。
　上の図は、合計が4から24になるさいころの組みあわせを書きだして、
　積み上げたものです。14を中心に左右対称の釣り鐘型があらわれました。
　
  つまり、正規分布に近い形です。これが、統計学的な事実です。

　機械部品の寸法や電気部品の特性に、そのばらつきの範囲をしめすために
使われるのが公差です。機械部品の寸法や、電気部品の特性のばらつきは
正規分布にしたがうことが多いのですが、なかには、一様分布するものも
存在します。

　公差の集積（複数の部品を組みあわせたとき、結果がどの程度の範囲をとるのか？）
を推定する技術を公差解析といいます。
  公差解析には、完全互換の方法と不完全互換の方法があります。
　完全互換の方法は、取る幅の最小値と最大値を計算する方法です。
　上のさいころの例でいえば、公差の集積結果は4～24になる、ということを
結論とします。
　一方、不完全互換の方法は、統計学を使って、一定の危険率のもとで、
取る幅の範囲を推定します。私は、こちらが正しいと考えています。

　ごくわずかな確率で発生する集積公差の最小値や最大値付近まで、考えて
いたのでは、個々の部品にあたえる公差をとても厳しくしなければいけません。
　当然、大幅なコストアップにつながります。
　そればかりか、設計自体が成り立たなくなることも起こりえます。

　どの範囲にすればよいのか？は統計学的な危険率をもとにすればよいのです。
　製品の品質水準を3σ管理としたいのであれば、両側の確率が0.135%程度に
なるように推定すればよいのです。

　完全互換の方法も行うべき、と指導される上司などもいることでしょうが
たぶん、その方は統計学をあまり知らないのでしょう。

 　昔、私は上司から、
「完全互換の方法でも・・・」といわれたのですが、さいころの事例を
説明したところ、納得していただきました。

ひさしぶりに技術的なはなし、しかも長文、最後まで読んでいただき、
ありがとうございました。

　ご質問などありましたら、コメント投稿してください。コメントは
公開しませんかｒ、ご安心ください。