2月26日に品質工学会からQES2015品質工学研究発表大会での発表採用通知が
来ました。品質工学会での発表は今回が初めてになります。
さっそく、論文の制作に取り掛かります。テーマはダーウィニズム（進化論）を使った
圧縮ばねの最適設計方法に関するもので、許容差設計によるSN比を活用するものです。
『圧縮ばねの設計』で紹介した設計方法に関するものです。自分としては、かなり有効な
設計方法だと思って自負しています。
さて、昨日ピザが急に食べたくなり、自宅から３分のところにある宅配ピザ屋さんにネットで
発注しました。注文ページから発注ページに遷移すると 『艦これキャンペーン応募』 という
チェックボックスがありました。これにチェックをいれて、時間通りに取りに行くと、ピザの
箱にカバーが ・・・ そして、クリアファイルもいただきました。
3月中旬からキャンペーンの第2弾が始まるそうです。
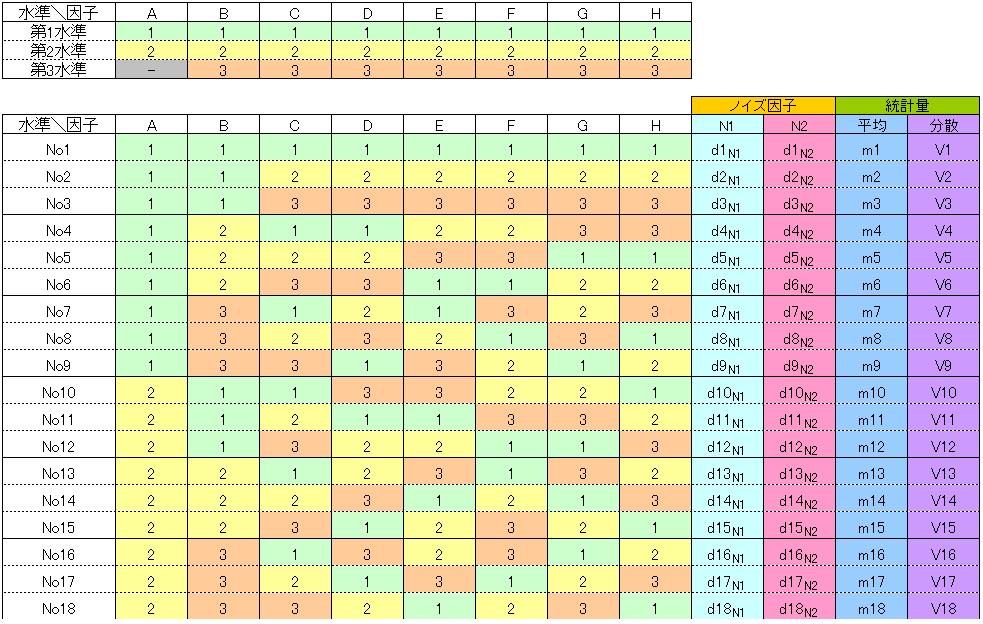
では、『ゼロ望目特性』の原理と計算式、そして、重大な制約条件について説明します。
たとえば、旋盤で棒材を切削してある軸を多数つくるとき、その全長が10ｍｍの軸と100ｍｍの軸のように違いがあっても、同じ旋盤で同じ作業者が同じ環境のもとで加工すれば、『望目特性』評価の感度に相当する全長の10ｍｍや100ｍｍという長さ違いに関係なく、どちらも、標準偏差；ｓ＝0.1ｍｍというような結果が得られることでしょう。『望目特性』評価では、当然、100ｍｍの軸のＳＮ比が20〔db〕（真値で100倍）高いという結果になりますが、これは合理的ではありません。
ゼロ望目特性のＳＮ比とは、正負の領域にまたがり、0（ゼロ）が理想値である特性を対象とした評価方法で、上の例では、図面指示の10ｍｍに対して多数ある個々の加工品の寸法がどれだけはずれているか、つまり、偏差；εを評価の対象とするものです。
さて、その計算式ですが、ｎ個のデータ； x1～xn が観測された場合、
そして、Ve＝Se/(n－1）という計算工程で誤差の分散；Ve を求めます。Veがゼロ望目特性のSN比の真値となります。SN比は大きいほどよいという思考をもとに、
と対数変換して表現します。
教科書ではよくゼロ望目特性評価の一例として、生産する鉄板のそりをあげていますが、つぎの事例で考えてみます。
鉄板を平坦に矯正するレベラーという機械が２種類あったとします。
Aのレベラーで平坦加工前の表面が塗装された100枚の鉄板から無作為に4枚抽出して加工したとき、表面を上にして凸側をプラス、凹側をマイナスと表現して、（＋2mm，＋1mm，－1mm，－2mm）という結果が得られました。
また、Bのレベラーで同様の加工をおこなったところ、（＋2mm，＋2mm，＋2mm，＋1mm）という結果になりました。
どちらのレベラーよいかをゼロ望目特性のSN比で評価しますが、まず、直感的にどちらがよいレベラーだと思いますか？
では、Aのゼロ望目特性のSN比を計算します。４つのデータよりSe=10となりVe=3.33になります。そして、対数変換したSN比は－5.23〔db〕です。一方、Bの場合、
Se＝0.75となりVe=0.25で対数変換したSN比は＋6.02〔db〕です。つまり、Bのレベラーのほうがゼロ望目特性の値が大きくなり「Bのほうがよいレベラー」という結論になりました。
いかがですか？違和感を覚えませんか？
実は、Bのレベラーの結果に対してゼロ望目特性で解析をすること自体が誤りであるためです。
ゼロ望目特性で公正に評価できるのは、対象とするデータ群が正負の領域にまたがり、その平均がゼロ（または、かぎりなくゼロに近い値）になるときのみです。Bのデータの平均は1.75（≠0）であり、ゼロ望目特性で解析すべきデータではありません。
このように、理想値がゼロだからといってやみくもにゼロ望目特性のSN比で解析するととんでもない間違いをおかす懸念があります。特にL18直交表などでは、制御因子・水準の組みあわせによって、平均がゼロにならない実験も十分ありえます。このとき、ゼロ望目特性のSN比の要因効果を計算しても、その結果は正しくありません。
では、「出力はゼロが理想値であるけれども、実験結果の平均がゼロにならない場合」どのような計算方法がよいか？
に関するひとつの答として、データとゼロの偏差を解析対象とする分散も考えられます。これは、結果的にデータの平方和をデータ数；ｎで割った結果です。（ｎ－１）ではなく、ｎで割るのは、データ平均との偏差の平方和の場合、自由度は（ｎ－1）になりますが、ゼロからの偏差の場合、どのデータも自由に決めることができるので自由度はｎになるためです。
平均を使うと、結果として得られた平均で拘束されるため自由になるデータの個数はｎ－1になります。
上の例では、Ａの場合、Ve＝2.5，SN比＝－3.98〔db〕、Bの場合、Ve=13，
SN比＝－5.12〔db〕となって、見かけ上Aのレベラーのほうがよい、という結論になります。見かけ上と書いた理由を次の例で説明します。
上の例にくわえて新しくCというレベラーで加工した結果、（＋2mm，＋2mm，＋1mm，＋1mm）になりました。この結果からVe=2.5，SN比＝－3.98〔db〕となり、Aと同じよさになります。はたしてAとCはおなじよさのレベラーと考えてよいでしょうか。
Aはそりの振幅（レンジ）が4mmです。一方、Cは1mmです。また、そりがプラスマイナス（凸，凹）がランダムに発生する可能性があるAに対して、Cはそりがプラス側（凸）だけです。そりをゼロにするための調整はどちらがやりやすいでしょうか。
この点を考えるとCのほうが優れている、という指標になってほしいのが実情です。
結論からいいますと、ゼロを理想とする特性を評価する場合であっても平均がゼロにならない場合は、望目特性のSN比で評価すればよいのです。SN比の真値をηとすると、
η＝m＾2 / σ＾2 で計算します。
L18直交表実験である実験がm=0やσ＾2＝0になると計算不能になってしまいますが、そのときは、ｍ＝0.00001 や σ＾2＝0.0001 などの値を仮に置数すれば計算ができます。
品質工学のユーザーにとっては、SN比の厳密な値がほしいのではなく、どの水準を採用すべきであるか？がわかればよいのですから。
前々回、望目特性のSN比に関する問題点を指摘しました。そして、その解決方法の
入口をつぎのブログでお知らせすると書きました。
しかし、その後いろいろと調査・検討した結果、前回指摘した問題よりも重大な問題を
発見しました。この問題はかなり大きく根が深いので、もっと時間をかけて検討する必要が
あるため、報告にはもう少し時間をいただきたいと思います。
そこで、今回は代打として『ゼロ望目特性』を使うときの注意を２回にわけて紹介します。
品質工学の静特性評価において、『望目特性』、『望小特性』、『望大特性』、『ゼロ望目特性』という４つのＳＮ比という評価指標が提案されています。
パラメータ設計ではおもに『望目特性』を使って制御因子・水準の要因効果を評価します。
評価対象となる出力結果（データ）が正の領域であり、その出力が小さければ小さいほどよい場合は『望小特性』のＳＮ比で、その逆に大きければ大きいほどよい場合は『望大特性』のＳＮ比で評価します。
では、建築物の強度はどの特性で評価するべきでしょうか。当然、建物は頑丈であるほど、地震などの災害に強いわけですから『望大特性』のＳＮ比で評価するべきであると思われるかもしれません。
ここで、ＳＮ比は品質の評価指標であり、品質工学では、品質を『製品が出荷後、社会に与える損失である』と定義しています。製品が出荷された後、社会に与える損失とは、
その製品に期待されている機能の発揮不全（ばらつきや故障）によりユーザーが被る実損失・機会損失、メーカー側での不具合対策、設計変更と改造・改図作業、設備や工程の修正、品質管理基準の見直し、そして、ブランド名の劣化などの損失、そして、公害です。
「製品が出荷後」ですから店頭在庫、ユーザー購入と輸送、開梱、使用、廃棄までに生じる上記の損失の全体が社会に与える損失です。
建築物の場合、廃棄とはその建物を壊して更地にすることです。このとき、『望大特性』のＳＮ比で評価された結果の建物は強度が高いので建物を解体ためにコストが多くかかります。そのことまで考えると、建物の強度は『望大特性』ではなく『望目特性』で評価して、想定される地震に対して必要十分な強度をもち、かつ、なるべく安いコストで解体できる強度を狙うべきであることになります。
『望小特性』、『望大特性』のＳＮ比では品質工学のパラメータ設計のうまみであるチューニングができない、という点も弱点になります。
さて、もうひとつ『ゼロ望目特性』のＳＮ比は、場合によっては評価対象を都合よく評価できる指標であり、私も実務ではよく使っています。しかし、『ゼロ望目特性』のＳＮ比には見落としがちな重大な制約条件があります。これを認識しないで『ゼロ望目特性』評価を実施すると、痛い目にあうこと間違いなしです。
次回、ゼロ望目特性の考え方と計算方法、そして、重要な制約条件について解説します。
18直交表を使ったパラメータ設計では、８個の制御因子（システムの構成要素）に２～３個の水準（構成要素の選択肢）を割りつけ、少なくとも２水準のノイズ因子環境下で１８組の実験ごとに２つ（以上）の実験結果を得る必要があります。
つぎに、１８組の実験ごとに得られた２つの実験結果の『平均；m』と『分散；V』を１８対計算します。
つづけて、18組の実験ごとに、『平均』の2乗を真値とする『感度』と、『感度』の真値を『分散』で割った結果を真値とする『望目特性のSN比』を計算します。
そして、各制御因子の水準ごとの『要因効果』を計算します。『要因効果』とは、その制御因子・水準がシステムの出力結果におよぼす影響の大きさです。『感度』と『SN比』両者の『要因効果』を計算します。L18直交表の場合、『感度』と『SN比』それぞれ、２＋３×７＝23個ずつの『要因効果』を計算します。
ある制御因子、ある水準の『要因効果』は、その制御因子、その水準が関与した実験を抽出して総和し、データ数で割る、つまり、平均を計算して求めます。たとえば、制御因子Bの第2水準に関する『感度』の要因効果は、実験No．４～６とNo．13～15の『平均』を２乗して総和し、６で割った値です。このような計算で『要因効果』が求まる理由は、システムの出力は、各制御因子の出力に関する影響の足し算で成りたっている、つまり、『要因効果』の加法性が成立しているという前提があるためです。
『要因効果』の加法性が成立するためには、各制御因子が独立している、つまり、制御因子間に交互作用がないことが必要条件です。
制御因子が独立していて、システムの出力がその効果の加法性で成立しているとき、18組の各実験結果は、各制御因子の水準の『要因効果』を足し合わせた結果になります。（実際はその値から全体平均の７倍を引いた値ですが。）
『感度』のもととなる実験結果の『平均』；mは加法性が成りたつため、『感度』の真値を常用対数変換した実用上の『感度』も加法性が成立します。
一方、制御因子が独立している場合、統計学上、『分散』；Vも加法性が成りたちます。
しかし、『SN比』の真値；ηは、η＝m＾2 / V で計算しますが、このとき、分数の分母は加法性が成立しません。
1 / 2＋1 / 3 ＝2 / 5 ではないのです。
つまり、『感度』の場合、18組の『平均』 から制御因子・水準ごとに『平均』の要因効果を計算して、そのあと、『平均』の『要因効果』を２乗して『感度』の真値をもとめ、常用対数変換した結果である『感度』には加法性が成立するのですが、18組の『SN比』から計算した各制御因子・水準の『SN比』の『要因効果』には加法性が成立しないことになります。
実務上実施したパラメータ設計では、『感度』は再現しやすいけれども『SN比』は再現しにくいという経験が多い気がしています。また、私の所属している地方研究会での報告でもその傾向が強いように感じていました。
これは、18個の『SN比』から計算した制御因子・水準の『SN比』の要因効果には加法性がない、ということが原因ではないかと考えています。
パラメータ設計では、実験と結果の解析を行なった後、『最適条件』と『対抗条件』の２つの確認実験を行い、『感度』と『SN比』の再現性をチェックして
1．実験が成功したといえるのか？
2．得られた結果を信頼してよいか？
の判断をすることになっています。
しかし、今回の内容のように、もともと一般的な品質工学流のやり方で計算した『SN比』には加法性が成立しないので、『SN比』の再現性が低かったとしてもそれほどがっかりすることはないと思います。『感度』の再現性が高ければ、実験は成功していて、得られた結果を信頼してもよい、ということでよいと思います。
では、どのように『望目特性のSN比』を計算したらよいか、ですが、現在まだよい方法が見つかっていません。ただし、新たな計算方法を見つける旅の入り口には立ったかな？と思っています。
その入り口について、次回報告します。
私が勝手に師匠と拝しております長谷部光雄先生が、先日、日科技連さんから
新書 『タグチメソッドのはなし』 を出版されました。
今回は拙書を参考文献として掲載していただきました。そのため、直接先生から
新書を贈呈していただきました。
先生は今まで品質工学やTRIZに関連する書籍をたくさん執筆されており、その
わかりやすさは定評があります。
さて、今回の『タグチメソッドのはなし』 を開くと ・・・
いままでの設計手法が通用しなくなった現在の技術活動の解説からはじまり、
品質工学のパラメータ設計の原理と進め方、活用方法、そして、損失関数の
解説とつづき、品質工学の目的が 『社会の総損失を最小化する』 ことである
ことの理解の導きまで、非常にわかりやすく書かれています。
そのあと、MTシステムの解説があり、最後は先生の 『一流の技術者』 についての
定義とそれを目指すために、若い技術者はなにをするべきか、が書かれてきます。
一気に読み終えてしまいました。
特に、一流の技術者になるための思考や心構え、行動に関する記述は、とても
すばらしい内容でした。まわりの同僚にも読んでもらいましたが、全員、おおいに
納得していました。
そして、『一流の技術者』 がうまれ、育つためには、彼が所属し活動している
『企業』 という環境が、単に 近視眼的な『利益追求』 に盲従してはだめで、
社会全体にたいする 『貢献』 という哲学に根ざした経営がなされていることが
必要条件であることを理解できます。
長谷部先生は、品質工学だけでなく、QCやTRIZ など技術者にとってとても重要な
汎用技術を駆使して技術支援のコンサルタントをされている方で、私は、品質工学
だけでなく、技術者の大先輩として尊敬しております。
先生のホームページをぜひご覧ください。
