D：ニース沖の超絶ドットストライプ： 海底考古学３７－D

D：ニース沖の超絶ドットストライプ：　海底考古学３７－D

 

 

 

もう一つ見てみよう。

　“X-2”　とした、いちばん下の　“交差ドットライン”　である。ここでは　“平行ドットストライプ”　との交差角度は　４５度前後　である。

 

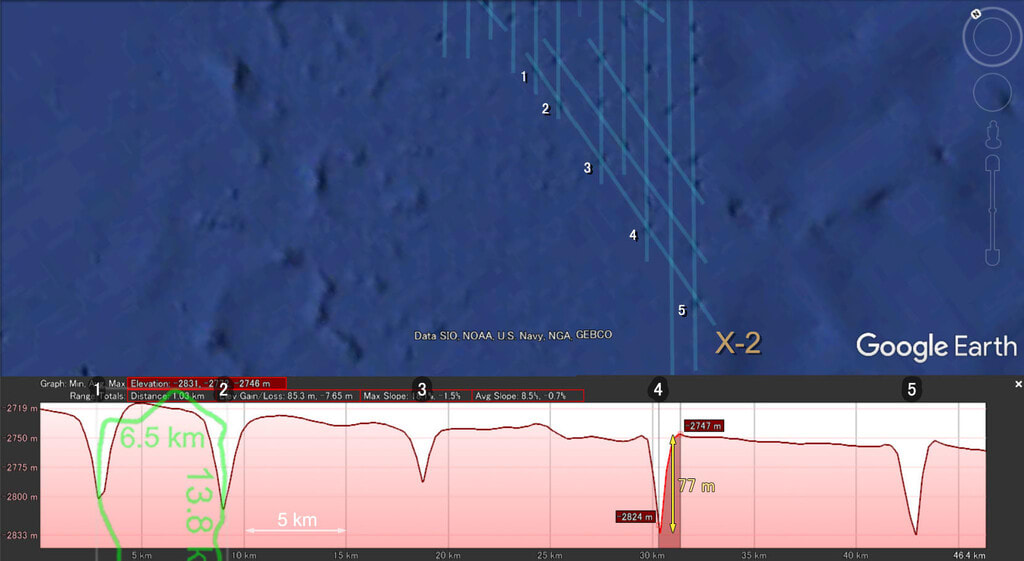
ドットは５つあり、すべて陥没ドットである。

ドット 1 と 2　の間隔は、交差している平行ドットストライプのインタバル１つ分である。ドットストライプの平行に走るドットラインの間隔は　約 3 km　であるが、この交差ドットラインはこの平行のストライプを斜めに突っ切っているので、ドット間の距離はゆうに　6 km　以上ある。上の画像の断面図をご覧いただきたい。山手線の横幅（6.5 km）に近い距離がある。

さて、ドット  2 と 3、  3 と 4、  4 と 5、のそれぞれのあいだの距離は、いずれもインタバル２つ分の間隔である。しかし、だからといって、これら３つの距離が同じというわけではないようだ。上の断面図を注意して見ると、右に行くにつれて間隔が広がっている。しかも、ドット１　から見ても、ドット間の距離は、ドット２，ドット３、ドット４、ドット５　と比例的に広がっているように見える。

インタバルの数で　“X-1”　と　“X-2”　を比較すると、以下のようになる。言うまでもないが、この２つの数列の間には何の関係もない。

“X-1” ：　　２，　　２，　　２，　　３，　　３，　　２　

“X-2” ：　　１，　　２，　　２，　　２

 

平行なドットストライプの個々のドットライン上に並ぶドットは、そもそもからして等間隔ではない。 平行ドットストライプの個々のドットライン上のドットは等間隔ではなく、一見ランダムなインタバルで並んでいるように見える。しかし、この直線上の一見ランダムなドットの分布も、純粋にランダムなものではなく、潜在的に何らかの規則性に従ったものである可能性もある。だからこそ、交差ドットラインが　“グループＸ”　としてまとまって成立するのかもしれない。

とにかく、交差ドットラインが平行ドットストライプを斜めに横切ると、その直線と平行ドットストライプの交点上に５つも、７つもドットがぶち当たるのだ。これが確率的にいくらでも起こることなのかどうかを検証する能力はあいにく持ち合わせていない。しかし、全体としてこの　“グループＸ”　の交差ドットラインの分布には、何らかの規則性があるように感じられないだろうか？

 

 

さて、交差ドットラインとして　“グループＸ”　のドットラインを見てきたが、実は交差ドットラインのグループはもう一つあるのだ。

以下では、平行ドットストライプ（A-D）をすべて水平の向きに直してある。下の左の画像は、上の１つ前の画像を時計回りに９０度回転させたものであり、“グループＸ”　の交差ドットラインがオーバーラップしている。

そして、下の右側の画像は、それにさらに　“グループＹ”　の交差ドットラインがオーバーラップしたものである。

 

平行ドットストライプ（A-D）と　“グループＹ”　だけにしたもの。

両者のストライプを比べると、その規則性（平行、等間隔）の差は歴然としている。にもかかわらず、“グループＹ”　には一貫した　“流れ”　があるように思える。

 

“グループＹ”　だけにしたもの。一部にはほとんど平行に並んだドットラインもある。しかし、ドットラインはすべて平行とはとても言えない。むしろ右下に向かってやや放射状に広がっているように見える。

 

以下は、上の画像をさらに拡大したものである。水平のドットラインにはあえて補助線は施していないが、　A-D　の平行ドットストライプ　であることはもうおわかりであろう。明白な水平のドットラインに交差して、斜め下に流れるようなドットラインの　“グループＹ”　を見つけていった過程が多少でもご理解頂ければ幸いである。

 

 

さかのぼるようで恐縮だが、ここで　“グループＸ”　のほうも同様にご確認いただきたい。

この画像をじっくりご覧いただければ、“平行ドットストライプ　A-D”　  にオーバーラップして、“グループＸ”　というドットラインの流れが潜在的に存在していることが、手に取るようにご理解いただけるはずだ。冷静な判断力の持ち主であれば、“グループＸ”　や　“グループＹ”　が、ザウルスが気まぐれで勝手に読み込んだものではないことが理解できるはずである。

 

 

ここで、“グループＸ”　のときと同様に、“グループＹ”　でも具体的に個々のドットラインを見てみる必要があるかもしれない。まず、数列の乗った　“Y-1”　を見てみよう。

“Y-1”

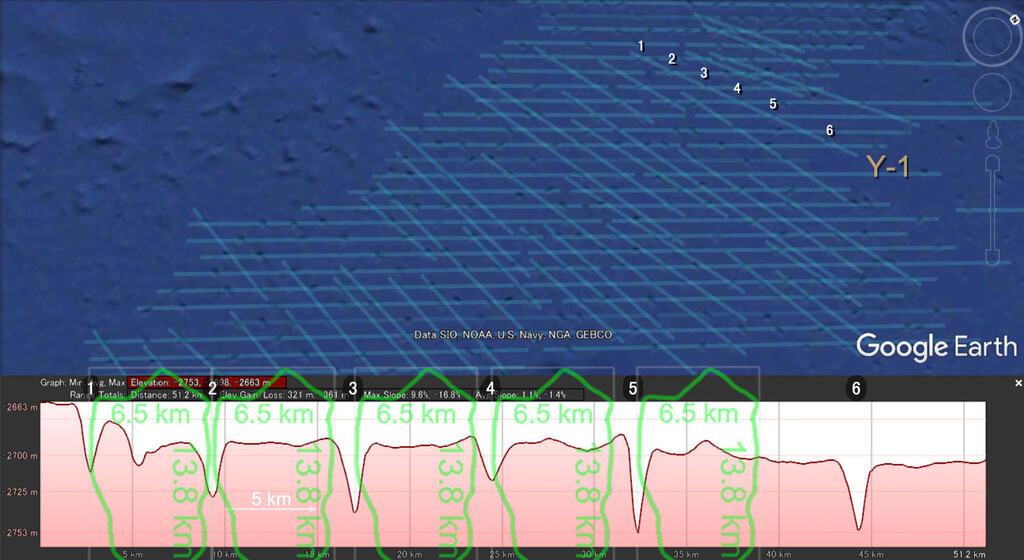
この画像のドット間の距離を注意深く見ると、まず、“ドット１”　と　“ドット２”　の間の距離は偶々（たまたま）であるが、山手線の横幅である　6.5 km　にほぼ等しい。そして、画像中の山手線の緑色のハラペーニョパターンを見れば、次の　“ドット２－３”　の距離は、それを若干上回っていることがわかる。

さらに、“ドット３－４”　の間の距離となると、“ドット１－２”　の距離よりも今度はやや狭くなっていることがわかる。

そして、次の　“ドット４－５”　の距離は、“ドット２－３”　の間の距離よりもやや上回っている。

“ドット１～５”　までは、交差する　“水平のドットストライプ”　のドットラインとは１行も空けずに交差しているのであるから、“Y-1”　の　“ドット１～５”　はすべて等間隔であってもおかしくはない。しかし、“Y-1”　の　“ドット１～５”　のドット間距離は等間隔ではなく、微妙に拡大しているのだ。

“ドット５－６”　の距離は、“水平のドットストライプ”　のドットラインのインタバル２つ分であるので、もはや垂直のハラペーニョパターンは役に立たない。

 

 

“グループＹ”　の中でもう一つ、　“Y-２”　を見てみよう。このドットラインでは、ドット２，４，５　はドットラインに辛うじてかかったような状態である。しかし、どんなに辛うじてであれ、とにかく真直線である補助線にかかったいじょう、ドットライン上にカウントされる。

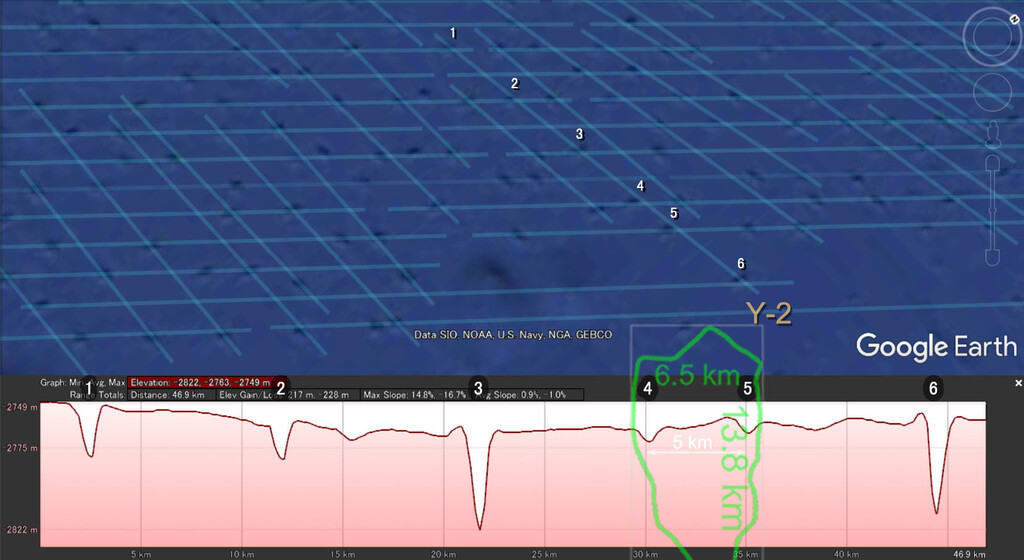
そして、“ドット間距離”　の　“１－２”、　“２－３”、　“３－４”，　“５－６”　は、“水平のドットストライプ”　のドットラインの、それぞれインタバル２つ分である。例外は　“４－５”　であって、ここではインタバル１つ分である。この例外的な　“４－５”　の距離は、ほとんど　5 km　であり、山手線のハラペーニョの幅よりも狭い。

 

さて、同じ交差ドットラインの　“グループＸ”　と　“グループＹ”　だけにして見てみよう。

たしかに、どちらのグループでも、その中のドットラインは　「すべて等間隔、かつすべて平行」　というわけではない。“平行ドットストライプ（A-D）”　に比べると、はるかに　“緩やか”　で、　“流動的”　であるように見える。

 

 

あらためて、３つを一緒に見てみよう。

 

たしかに、“グループＸ”　と　“グループＹ”　の客観的な規則性　については、議論の余地があるかもしれない。ザウルスの主観的で恣意的なドットの選択によって作り上げられた、一見規則性のあるようにも見えるドットラインの集合に過ぎないのかもしれない。（笑）

 

この問題に関しては、解決できる可能性は十分にある。数学的、確率論的に解析すれば簡単に答えは出るだろう。

 

A-D：  所定の面積中の約500の点の分布が、自然状態で、等間隔かつ平行なストライプ（グループA-D）を形成する確率。ただし、ドットライン上のドットの間隔は等間隔ではなく、“ランダムに見える”。

 

X, Y： 上述のような点の分布が、同時に、一見規則性のあるように見える　“グループＸ”　と　“グループＹ”　を形成する確率。および、同様に一見規則性のあるように見える　“他のグループ”　が成立する可能性とその実例の証明。

 

あいにく、ザウルスは以上のような数学的、確率論的な問題を解決する能力に恵まれていない。誰か、そういった方面のキャパシティを有するひとにお願いする他はない。

 

ただ、“グループＸ”　と　“グループＹ”　の客観的実在性は、実は些末な問題であるとも言える。両グループの客観的実在性が仮に１００％否定されたとしても全然かまわないのだ。ザウルスの主観的願望の投影に過ぎなかったとしても一向にかまわないということだ。（笑）　

仮に　“グループＸ”　と　“グループＹ”　の客観的実在性を否定しようとしたら、そのためには　“グループA-D”　の実在性　を前提にすることが不可欠ではなかろうか？（笑）

たしかに、“グループＸ”　と　“グループＹ”　は　“おまけ”　である。無くても大勢（今回の最重要の事象）、つまり、“グループA-D”　の実在性、の証明にはあまり影響はない。しかし、“グループA-D”　をよりよく理解しようとするならば、　貴重な　“おまけ”　であるはずだ。（笑）

 

 

要するに、問題は、以下の等間隔、かつ平行なストライプ（“グループA-D”）の存在なのである。

 

しかし、これは、あらゆる議論以前にすでに客観的に実在しているものである。一部の人たちが必死に、ザウルスの主観的願望の投影として片づけようとしても、誰でもグーグルアースによって、その存在を容易に確認できてしまうものである。（笑）

 

“グループＸ”　と　“グループＹ”　は、もしかしたらザウルスの　“妄想”　として説明できるかもしれない。（笑）　しかし、“グループA-D”　を同列に同じように片づけることができると考えるのはナイーブに過ぎるだろう。

 

この海底の巨大痕跡、“グループA-D”　は、客観的、物理的、立体的に実在しているものであり、その存在はどう足掻いても否定しようのないものである。違うだろうか？（笑）

すでに見てきたように、この海底の巨大痕跡の規模はとてつもなく巨大で、人間的スケールをはるかに超えている。人間的スケール、人間的な尺度をあまりにも超越しているために、普通の人間にはすぐには受け入れられないものである。

しかし、それは現実に存在しているのだ。多くのひとが必死に目をそむけても、それは存在し続けている。（笑）

 

 

“超絶ドットストライプ”　と呼ぶ理由：

１）　１本の　“真直線のドットライン”　上にドットが１０個も２０個もある。

２）　そうした　“ドットライン”　が、限られた海域に何十本もある。

３）　それらの　“ドットライン”　は、すべて　“平行”　である。

４）　それらの　“平行なドットライン”　は、すべて　“ほぼ等間隔”　である。

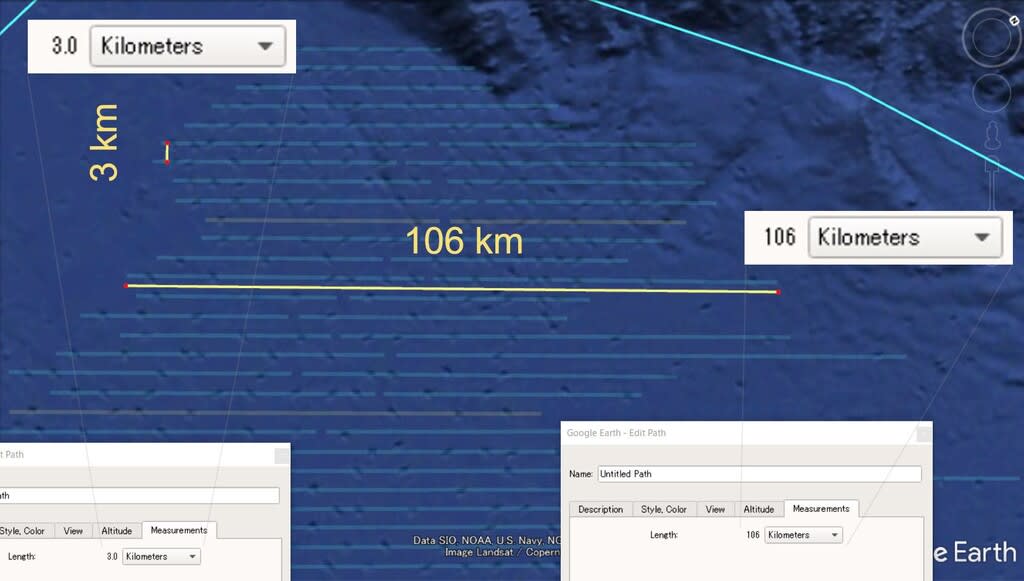
５）　“ドットライン”　の数はおよそ３６本ある。　平行なストライプの間隔は平均　3 km　ある。　“ドットライン”　の長さはおよそ　100 km　ほどある。総じて全体としては、とてつもなく巨大な痕跡である。

 

「遺跡」　ではなく、“痕跡”

自称研究者や大学教授などが海底に巨大な何かの痕跡を見つけると、「遺跡」だの、「都市遺跡」　などと言っているのをウェブサイトや動画で目にすることがある。

 

「海底考古学」　は、海底のさまざまな　“痕跡”　を対象にしてはいるが、「遺跡」　という言葉を使うことはない。「海底考古学」　が対象とする　“痕跡”　が　「遺跡」　であるという確証も得られないし、そう主張するだけの証拠もないし、そもそも　「遺跡」　の一般的な定義にどれだけ当てはまるか疑問だからである。

ウィキペディア　による以下の定義は、ごく一般的なものであるが、「海底考古学」　が対象としているものは下線部分に該当すると考えられなくもない。

「遺跡（いせき）とは、過去の人々の生活の痕跡がまとまって面的に残存しているもの、および工作物、建築物、土木構造物の単体の痕跡、施設の痕跡、もしくはそれらが集まって一体になっているものを指している。（後略）」

まず、「遺跡」　は　“痕跡”　だと言っている。その通りだ。しかし、“何の痕跡か？”　が問題である。例えば、「ビーバーの作ったダム」　は　ビーバーの営みの　“痕跡”　である。

しかし、いくら古びて　“廃墟化”　していても　「遺跡」　とは言わないだろう。なぜならば、人間が作ったものではないからだ。「遺跡」　以前に、「考古学」　じたいが、そもそも人文科学の一分野として成立しており、人間以外による　“痕跡”　はどだい対象外なのだ。動物による痕跡であれ、人間以外の知的生命による痕跡であれ、想定外なのである。

今回の　“ドットストライプ”　にしても、「人々の生活」、つまり　“人間の営み”　を反映したものかどうかは極めて疑わしい。率直に言えば、その可能性はゼロと思っていい。（笑）

「海底考古学」　が対象とする痕跡はあまりにも巨大で、人間的な尺度をはるかに超えているために、人類史を前提にした考古学の概念をそのまま流用することには、誤解と混乱を招くおそれが多分にあるだろう。「海底考古学」　では、「遺跡」　という言葉は当面使用する予定はない。“痕跡”　で十分である。人間中心主義的な観念にまみれた　「遺跡」　という言葉、概念を敢えて避けて、当面は　“痕跡”　でいくつもりである。

さて、これらの　“ドット”　、“ドットライン”、　“ドットストライプ”　は　“自然力だけで出来たもの”　であろうか？

もし、地上に同じようなものがあったら、どうだろうか？自然力によって天然にできた　“自然の造形”　と見なされるであろうか？アマゾン川やロッキー山脈やグランドキャニオンと同列のものであろうか？

 

 

「海底考古学」の読者は決まって以下のような質問をぶつけられる、とすでに警告した。（笑）

“今回の　“超絶ドットストライプ”　と呼ぶ海底の巨大な痕跡は、自然に出来たものだと思いますか？

 

●「イエス」　と答えるひとに：　　「それならば、どういったメカニズムで出来たと思いますか？　どんな自然力によって出来たと思いますか？」

→　コメント欄を使って、あなたの　“自然造形説”　を聞かせて頂きたい。

 

●「ノー」　と答える人、つまり　“自然造形説”　を否定する人に：　　「それでは、これらは人間によって作られたものだと思いますか？　それとも、人間以外の存在によって作られたと思いますか？」　

→　コメント欄を使って、あなたの　“工作説”　をぜひ聞かせて頂きたい。