私が中学生のころ、米ソが冷戦状態でした。
おたがいに、宇宙空間に偵察衛星を周回させ、相手の動向を監視している
状況でした。
当然、偵察衛星に監視されるのはいやですから、偵察衛星に近づき、自爆して
偵察衛星を破壊する衛星が開発されました。
この衛星をキラー衛星といいます。
さらに、このキラー衛星を攻撃するキラー・キラー衛星が開発されました。
衛星 ・・・ 星だけにキラ・キラです。
そして、キラー・キラー衛星を攻撃するキラー・キラー・キラー衛星も投入され
この連鎖に歯止めがかからず、最終的にはキラーが4376個つづいた衛星が
冷戦終結直前に軌道に乗ったそうです ・・・ というのはウソですが。
このようにある技術に対してそれに対抗する技術、さらにその技術に対抗する
技術が開発される、という ”いたちごっこ” が技術の進歩の源泉のひとつです。
みなさんのパソコンにもウィルスソフトの検疫・駆除をするためのワクチンソフトが
インストールされていると思います。
日々、新型があらわれるウィルスソフトに対抗するために、日々研究者、技術者が
頭と体を使っています。まさに、いたちごっこです。
現在は大手数社が独占的に開発・販売しているワクチンソフトですが、これを
開発している企業が本業以外に研究すべきものはなんでしょうか?
それは、たぶん、非常に強い感染力をもち、パソコンに致命的な障害をあたえる
ウィルスソフトなのではないでしょうか。
もし、これが開発できれば、ウィルスソフトのシェアを劇的に増やすことができて
大きな利益をあげることができるはずです。
第3者を装ったり、使ったりすることでこのウィルスをばらまけば ・・・
その企業だけが短時間でそのウィルスに対応できるアップデートができます。
なにしろ、ウィルスソフトの構造を熟知しているわけですから。
次回は技術者が自身の仕事の対象以外に研究しなければならないこととは?
を私の視点から紹介します。
品質工学のパラメータ設計で感度やSN比の要因効果をもとめる計算工程が
はらんでいる問題を提起することになるので、この内容を紹介することには
ためらいがありましたが、やっぱり有益な情報になると思いますので、
勇気をもって書きます。
今週、若い同僚がBlueToothによる機器間の通信特性を評価していました。
通信機器同志の方向と距離を変え、それぞれの組みあわせで数回ずつ計測し
その結果をまとめていました。
計測結果は計測器から出力される減衰率でdB(デシベル)表示でした。
彼は、ある条件で計測した複数の結果を算術平均してその条件での減衰率と
していました。
実はこの平均の計算には大きな間違いがあります。
解析対象が非常に広い範囲(たとえば0.001~10000のような)を取る特性を
評価するには10のn乗という指数表示にすると人間にとって認知性が高まります。
上記( )内の例ではnは―3~4 になります。
減衰や増幅の比率はこのnの値をB(ベル)という単位で表現します。しかし、
認知性の分解能を高くするために、nの値を10倍して表現します。これが
dB(デシベル)です。dl(デシリットル:100ml)と同じです。
さて、二つの増幅比があり、その平均が10dBであった場合、もとの二つの
デシベル値は、
①10dBと10dBの場合、②9dBと11dBの場合、③5dBと15dBの場合など
です。どの場合も平均は10dBになるのですが、対数変換する前の真値で考えて
みると、
①は10倍と10倍 ②は12.59倍と7.94倍 ③は31.62倍と3.16倍 です。
そして、その真値の平均は
①は10.00 ②は10.27 ③は17.39 になります。そしてこれをデシベルに
なおすと
①は10 ②は10.11 ③は12.40 となります。つまり、デシベルで表示されている
特性はそのまま平均してはいけない!ということです。
もし、平均を取る必要があるのなら、一度真値にもどし、それを平均し、対数変換
してデシベル表示にする必要があります。
同僚にこれを指導したところ、とても感動しているようでした。
そして、別の同僚もデシベル表示されている伝達関数の重心をもとめる作業を
していたのですが、彼にもこの内容を指導しました。
同源の問題をはらむ事象が2日つづけて起こったので、この内容は部内で
共有しようと資料作りをしています。
さて、今回の記事の冒頭部分、パラメータ設計の感度やSN比要因効果の推定は、
デシベル表示されている複数の結果の算術平均です。
パラメータ設計の場合、平均の対象となる複数の結果には問題となるほどの
大きな差はないので、まぁ、大きな問題はでないでしょうが、パラメータ設計の
要因効果の計算工程にはこのような問題があることを認識しておいたほうが
良いと思います。
さて、本日は毎年恒例のチャリティー番組の放送日です。
いつもウォーキングの帰りに通らせていただいている「日産自動車本社ギャラリー」
の通路からの画像です。
ここで、チャリティー番組のロケがあるようで、準備が進められていました。
証明の高櫓が2本くまれていましたが、そのうえで働いていた4名の技師の方は
みなさん女性でした。
櫓の横のモンキーステップを軽々と上り下りしていました。

黄色のTシャツも待機しています。
前回 真のナイキストサンプリングとはどのようなものか?を説明しました。
そして、真のナイキストサンプリングがなされていないと、FFTして得られた
周波数とパワーの情報は正確ではなくなる、ということも説明しました。
また、窓関数の性質についても少し説明しました。
今回は、多くの方(その中にはFFTを指導されている方も)が誤解している内容について
紹介します。
一般的に、なにかを観察するときには、なるべく細密に調査する、つまり、分解能を
高くして観察したほうが、観測対象の特性や状態をより詳しく把握できます。
FFTの場合もそうでしょうか?
前回のようにサンプリング間隔を1〔msec〕(サンプリング周波数:1kHz)でメガネ型の
サンプリング結果となるsin波の周波数は499.969481Hzです。
この周波数の1/4程度の周波数は約125Hzですから、125Hz程度のsin波を同じ
サンプリング間隔でサンプリングすると、499.969481Hzの4倍の観測密度になります。
こちらのほうが、より正確に観測対象信号の特性をとらえることができそうですが ・・・
信号の開始点と終点がゼロになるような125Hzに近いsin波の周波数は
124.9732963Hz になります。
上のグラフの左側最上段が1msecのサンプリング間隔でナイキストサンプリングできる
499.969481Hzのsin波を2の15乗(32768)個サンプリングした結果です。
左側2段目は1周期を4倍の観測密度でサンプリングできる124.9732963Hzのsin波を
2の15乗個サンプリングした結果です。ともに実効値は1V です。
それぞれのグラフの右にはその信号を矩形窓でFFTした結果を表示しています。
真のナイキストサンプリングができている499.969481Hz のsin波をFFTした結果の
スペクトルのピーク位置は499.9695Hzで、ピーク値は1.000V と、正確に波の
特性をとらえることができています。
しかし、124.9732963Hzのsin波を矩形窓でFFTした結果のスペクトルはすそ野が
若干広がっています。そして、スペクトルのピーク位置は124.72534Hz、ピーク値は
0.974V となって真のナイキストサンプリングができている信号の観測結果よりも
若干精度が悪くなっています。
観測密度を高くしても、波の特性は正確につかめるわけではありません。
メガネ型のサンプリング結果になったとき、もっとも正確にその波の特性を把握できる
のがFFTという信号処理です。
左側3段目は両者の信号を足すことで合成した信号です。
その右はこの合成信号を矩形窓でFFTした結果です。二つのピークはそれぞれの
sin波をFFTして得られた結果とぴたりと一致しました。
つまり、複数の異なる周波数のsin波を合成して得られた信号をFFTすると、もとの
単独のsin波をFFTした結果と一致します。
左最下段は合成信号のスタート部分の拡大、その左は合成信号の500Hz付近の
FFT結果のスペクトルです。
次回はメガネ型以外のナイキストサンプリングの特徴について紹介する予定です。
前回、サンプリング間隔1msec(サンプリング周波数1kHz)で499.9Hzのsin波(緑)と
499.964Hzのsin波(黄色)を32768(2の15乗)個サンプリングした下図の結果を
示しました。

これをFFTするとどうなるか?その結果を示します。
まず、両端は強制的にゼロにする矩形窓という窓関数と、最も一般的なハニング窓でFFTした結果です。
上から499.9Hz を矩形窓でFFTした結果、499.9Hz をハニング窓でFFTした結果、499.964Hzを矩形窓でFFTした結果、
最後が499.964Hz をハニング窓でFFTした結果です。
sin波の振幅は±√2(1.4142)Vですから、実効値は1V になります。
各グラフとも縦軸は0.2V/div で表示しています。
499.9Hzを矩形窓でFFTした結果はスペクトルのすそ野が広がり気味で、縦軸の実効値は0.9V 程度です。
また、それをハニング窓でFFTした結果は、スペクトルのすそ野が広く、さらに扁平でひすみがあり、実効値は0.5V 弱です。
一方、499.964Hzを矩形窓でFFTした結果は、FFTtが尖頭的であり実効値はぴたりと1V です。
しかし、ハニング窓でFFTした結果は少しすそ野が広がりひずみがあり、さらに実効値は0.5V ちょうどです。
これらの結果から、FFTして源信号の実効値が正確に分析できるのは、対象信号を2のn乗個離散的にサンプリングして
その両端がゼロであり、信号の周波数とサンプリング周波数の関係が499.964Hzと1kHz の場合のような特別な関係に
あるときだけです。めがねのように見える観測結果の場合だけです。
ナイキストサンプリングとはただ単純に信号周波数の2倍よりちょっと早い周波数で
サンプリングすればよい、ということではありません。
めがねのように観測するのが本当のナイキストサンプリングです。
ハニングなどの窓関数を使ってもこの問題を解決することはできません。窓関数は、横軸(周波数軸)の情報をなるべく正確に調べるために使います。
つまり、ある信号をあるサンプリング周波数で観測したとき、偶然にめがねのように観測できる周波数成分が存在すればその成分の実効値は正確に計測できるということです。
多数のsin波で構成されている信号の場合、FFTの結果の縦軸の意味は非常に希薄なものになってしまうのです。
次回は、この内容をもう少し深堀してみます。
今、会社の業務で新人の同僚と筐体の音響伝達特性を評価中です。
伝達関数やFFTについて彼に教えています。
どんどん知識を吸収してくれるので、教えるのが楽しいです。
さて、デジタル信号処理でもっとも有名なもののひとつがFFTです。
高速フーリエ変換(Fast Fourier Transform)は観測された信号に含まれる
周波数成分をスペクトルとして抽出するものです。
すべての波は複数のsin波で合成できるというフランスのフーリエの仮説に由来した
周波数分析技術です。
FFT解析ができる条件として、
・ 2^n 個のサンプルで構成されている信号であること。
・ 信号の開始点と終点が同じ値をとる周期関数であること。
の2つを満足していることです。
二つ目の条件を満足するために観測された生信号に窓関数を掛けることで
信号の前半部分と後半部分を徐々に減衰させ、1番目の信号値と最終の信号値を
ゼロにしてつなぐ、という処理をします。
信号のサンプリング周期も重要な要件であり、注目する信号成分に含まれている
であろう周波数の2倍よりやや早いサンプリング周波数で観測することにより
その周波数のスペクトルを得ることができます。
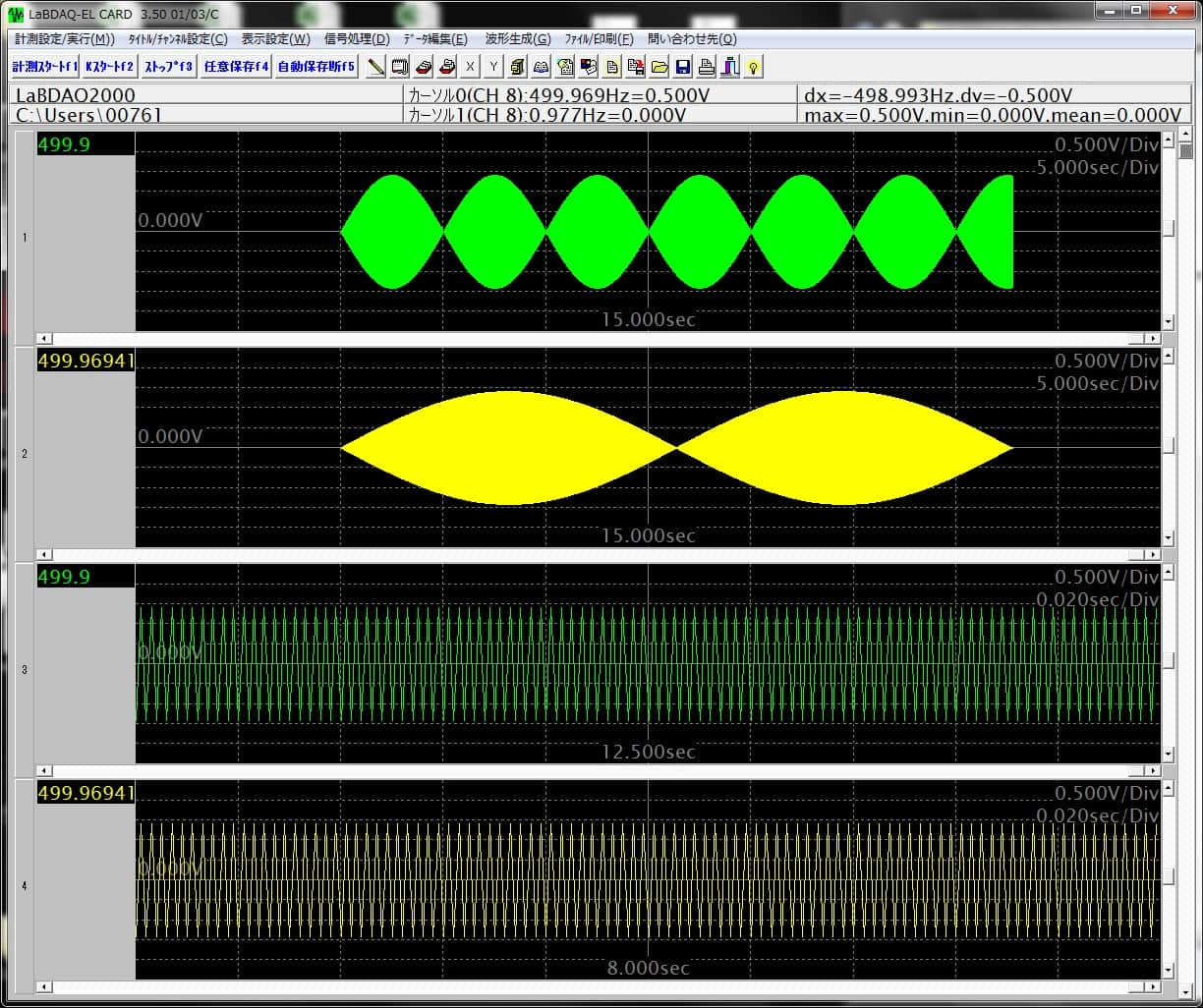
下の図の一番上のグラフは1kHzのサンプリング周波数で499.9Hzのsin波を
観測した結果です。
2番目は499.6941Hzのsin波を観測した結果です。
ともにサンプル数は2^15 (32768)サンプルです。
3番目、4番目のグラフは両者を拡大表示したものです。
団子やサングラスにみえるグラフは、このようなぎざぎざの連続になっています。
さて、両者をFFTするとどのような結果になるでしょうか?
そして、ナイキストサンプリングに関して、多くの技術者が大きな勘違いをしている
という現実・・・
それは、次回に・・・









