あったかい紅茶を
すすりながら、
エスタの屋上
「空のガーデン」で
見上げた札幌の青空を
思い出しつつ。
π のことを考えるともなく
考えつつ。
ヨドバシカメラのほうは
決まったようですが。
次に札幌へ戻ってくる時、
またこの眺めに会えるのかな。
予定では、
この窓の真ん前に、
完全に眺めを塞ぐ形で、
ビルを建てるそうで。
築20年とはいえ、
このJRタワー、
まだまだ現役のはずなんだけど。
頭のなかには、
今、円が浮かんでいて、
例によって、半径rと、
1回転した2π (rad)があり。
その差は2π-6rだなと。
(ブラウザによりパイが n みたいに
表示されたりします)
角度と長さとを
ゴッチャにしていいのかと
思いつつ(笑
その差が1rや π になるには、
何回転すればいいのかな?
その差がパイになるとき、

ネットは便利になったもんで。
極限の計算機まであるわ。
それによると、
+∞の世界じゃ、
π は3でいいらしい。
その差が 1 になるときも、
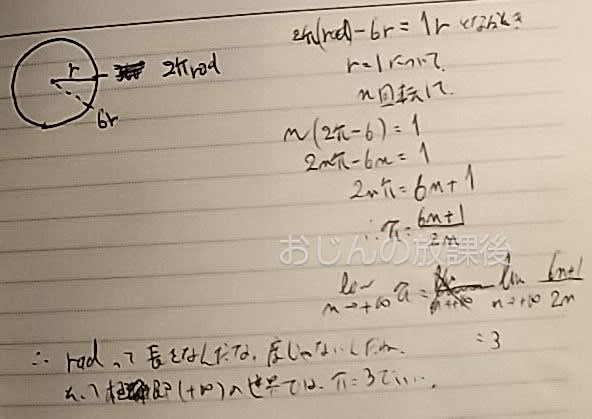
結果は同じになる。
なんか……
ラジアンって角度だって、
学校で教わったけどさ。
長さなんだなと。
そして、十進法の世界の、
11にあたる数は、
π の世界だと、
3なんだなと。ちなみに、
3.1415までの近似のとき、
n≒11.1001
面白いことに、5桁以上、
小数ケタを増やしても、
3.1415までしか表現されない。
それより先は、
僕らの数学の解像度よりも
細(こま)いんだろね。
曲線を直線に落としてるから、
これ以上の精度はたぶん、
2次以上の関数になるだろな。
それにしても、11回まわすとか、
何て中途半端!
そしてこの中途半端さが、
古典から現代に至るまで、
あらゆる数式のなかに
潜んでるんだろなぁ。
たぶんね、
円は半径とかから
入っちゃダメなんだろうな。
うん……
数遊びはいいね。
日常を忘れて、
自分を取り戻せるから。