数財探掘：【第25回】データマイニング・夜話(その七：情報量（エントロピー）の話）

エントロピーという単語を聞いたことがあるでしょうか？英語の得意な人でも難しい単語の部類に属するでしょうね。 この単語の意味を理解してもらうには、順序を追って説明する必要があります。

まず、次の単語を見てください。「道路」「みち」、「拡張」「ひろげる」。私たちには、それぞれのペーアの単語は全く同じ意味であることがわかりますが、日本語を全く知らない人にはどのように感じるのでしょうか？ローマ字で書いてみましょう。「doro」「michi」「kakucho」「hirogeru」。これらの音はお互いに全く違いますので、とても同じ意味をもった単語とは思えないでしょうね。

日本語にこのように『漢語』（外来語）と『やまとことば』があります。本来漢語は外来語ですが、あまりにも歴史が長いため、もはや外来語ではなく日本語と感じがちですが、本来は中国から渡来したれっきとした外来語です。

これと同じように英語にも英語本来のことばと外来語があります。例えば『魔法にかける』あるいは『うっとりさせる、魅了する』というのは英語では本来、 bewitch といいますが、フランス語経由から入ってきた外来語では enchant と言います。

英語に入った外来語にもいろいろな系統があります。例として私が高校生の時に非常に理解に苦しんだ英単語の話をしましょう。 それは experiential と empirical です。辞書を引くとどちらも『経験的な』という意味だと書いてあります。意味が完全に一緒なのにどうして二つの単語があるのだろうか？ あるとしたらどういう意味の差があるのだろうか？と随分悩んでいました。当時は語源まで遡って見ていなかったのですが、十年近く前にギリシャ語とラテン語を独習してようやくこの疑問が解けました。つまりこれら二つの単語は由来（出身地）が違うのです。

experientialは元来がラテン語（ex + periri）であり、empiricalはギリシャ語（en + peira ）であったのです。これらの後半部分（periri, peira）はどちらも『試みる, try』と同じ意味ですが、おもしろいことに、この前半の接頭辞（ex, en）は全く反対なのです。 ex は『外に』という意味であすが、 en は逆に『内に』という意味です。つまりラテン語の experiential では経験する、と言うのは、外界に向かって行う行為を指し、ギリシャ語の empirical では、行為によって自分の中に取り込む知識や経験のコンテンツを指す、と考えられそうです。物の見方が違うのに同じ意味を持つというのは面白いですね。

さらに難しい言葉ですが、瀉血（しゃけつ）という言葉があります。ヨーロッパでは古代ガレノスの時代から病気は過食が原因であると考えていたようです。それで、血を放出することで、その余分な栄養を体外に追い出すことで病気を治そうと考えていました。安土時代に日本を訪問したザビエルも日本を去ったあと中国で病気になりますが、その時の治療方法が瀉血でした。瀉血で治るどころか却って体が弱って亡くなってしまいました。この瀉血を英語ではbloodletting といいます。これは直感的に理解できる単語です。しかし、医学用語では phlebotomy といいます。これは元来ギリシャ語ですが、2つの単語から成り立っています。 phlebo + tomy (phlebo = 静脈、 tomy = 切断）瀉血を静脈を切るとみなすか（ギリシャ語）、血が流れ出る（英語）と見るかという観点の違いのようです。

更に、エピソードというのも意味深な言葉です。episodeは分解すると epi + eis+ hodos （in addition + into + way = at the entrance）という単語から成り立っています。日本語に直訳すると『入口のあたりで』となります。日本の住宅で、玄関の上がり口があり、ご婦人方がよくご近所の人たちと、いろいろとあることないこと噂ばなしを、駄弁っていますが、それがエピソードだという訳です。

このように、英語の難しい単語も分解してみればなかなか味わい深いものだと分かるでしょう。さて、ここまでで英語の単語にはギリシャ語経由の単語あることが分かって頂けたことと思います。 いよいよ本論に入りますが、データ解析の世界でよく使われるエントロピー（entropy）という単語はギリシャ語をベースにして近年新たに作られた造語です。

エントロピー（entropy）を分解すれば、 en + tropy（in + turn）となります。これは、1865年に Rudolf Clausius というドイツの科学者によって命名されました。エネルギー（ energy = en + ergon = at + work）という単語をまねて作ったようです。 エントロピーというのは元来熱力学の単語で、気体や液体が外から熱を（物理的単語では『仕事』）を受けたときに内部変化する量をさします。しかし、この本来の定義よりは、むしろ物体の内部状態の乱雑さを表す指標として一般的には知られているようです。

非常に抽象的なので、目に見えるエントロピーの例を挙げましょう。西部劇には砂金取りが登場しますね。川で砂利をすくい、ふるいにかけて、砂金を選別します。このプロセスを考えると、砂利と金が混在している文字通り玉石混淆の泥から砂金と砂とを別々にするわけです。混沌状態、つまりエントロピーの高い状態から金と砂利を分ける、つまりエントロピーの低い状態、に遷移させることで有益な資源、つまり金を取り出す訳です。

さて、情報理論におけるエントロピーは次の式で与えられます：


　 ここで p は事象の発生確率です。log の底は2です。

この式の意味するところを考えてみましょう。

週末に彼女とデートすることになったとしましょう。晴れると海水浴に行く、雨なら映画館に行くと決めたとしましょう。さて、週末には台風が来そうですが進路によっては晴れる可能性もあるとしましょう。この様に、晴れか雨か全く不明な時は、エントロピーがもっとも高い状態です。

先ほどの情報エントロピーの式を使って天気エントロピーを表わして見ましょう。天気は晴れか雨の二つの可能性（発生事象）しかありませんので、天気エントロピーは次のような式で表せるはずです。

　 天気エントロピー　= - {（晴れの確率） * log(晴れの確率) +（雨の確率） * log(雨の確率)}


台風のため週末の天気が全く分からない時、つまり晴れるかもしれないし、雨が降るかもしれない時は晴れと雨の確率が半々ですので、

　 晴れの確率 = a = 0.5、雨の確率 = b = (1 - a) = 0.5 となります。

これから、天気エントロピーは

　 天気エントロピー = - {0.5 * log(0.5) + 0.5 * log(0.5)}
　　　　　　　　　　　= - {0.5 *(-1) + 0.5 * (-1)}
　　　　　　　　　　　= 1


つまり全く不確定の時は天気エントロピーは1となります。 さて、週末の前日に天気予報では台風はどうやらそれそうなので明日は晴れの確率が70%、雨の確率が30%と出ていました。そうすると

　 晴れの確率 = a = 0.7、雨の確率 = b = (1 - a) = 0.3 ですから

　 天気エントロピー = - {0.7 * log(0.7) + 0.3 * log(0.3)}
　　　　　　　　　　　= - {0.7 *(-0.51) + 0.3 * (-1.74)}
　　　　　　　　　　　= 0.88

となってエントロピーが1から0.88に下がりました。つまり有用な情報を得たのでエントロピーが下がったのです。

週末の当日の朝、台風が全くそれて、海水浴には絶好の快晴になりました。雨の降る確率はゼロです。そうすると
　 晴れの確率 = a = 1.0、雨の確率 = b = (1 - a) = 0.0 ですから

　 天気エントロピー = - {1 * 0 + 0 * log(0.0)}
　　　　　　　　　　　= 0.0

つまり天気エントロピーはゼロ、一番低い値です。もっとも確かな情報を得た時、エントロピーはゼロとなります。



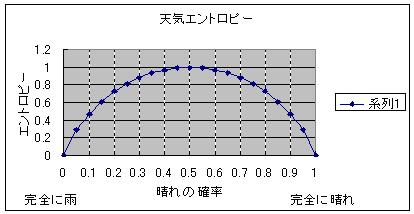
これを図示したのが、この天気エントロピーのグラフです。

データ解析というのが本来雑多なデータからあるまとまった知見を引き出すという行為ですので、エントロピーを減少させる行為に他なりません。つまり、雑多なデータをエントロピーの少ない状態に移行することが、情報を得ることなのです。

　 続く...