先にアップしました、経済成長と環境汚染に関して “環境クズネッツ曲線” という記事の中で調べていましたら、
掲題の “ジニ係数” というのが出て来まして、こちらも興味ある内容ですので、少し深堀してここに紹介しました。
長いですが、お付き合いください。
ネット記事から理解すれば・・・
ジニ係数(Gini coefficient, Gini's coefficient)とは、所得や資産分配の不平等を計るときに使われる指標である。
係数の範囲は 0から1 で、係数の値が0に近いほど格差が少ない状態で、1に近いほど格差が大きい状態である
ことを意味する。 例えば、ジニ係数=0 のときには完全な “平等” つまり皆同じ所得を得ている状態を示す。
逆に、一人がすべての収入を独り占めして残りの人が所得ゼロのときは ジニ係数=1(完全な不平等)となる。
通常はその中間の値で、値が大きいほど不平等であるということになります。
UNDPのHuman Development Report 2010にデータのある135カ国について、 横軸に一人当たりGDP
(対数変換したもの)、 縦軸に所得についてのジニ係数をとった散布図をつくってみると次のようになります。
ここで、ジニ係数0~1の値を100倍して0~100の値に変換しています。
図 135か国の所得とジニ係数
 (ネットより)
(ネットより)
図のプロットは、ばらつきは大きいですが、二次曲線で近似すると上に凸の曲線が得られます。
一人当たりGDPの対数値が3未満の国(GDPが1000ドル未満の国)ではジニ係数は40前後ですが、
GDPの対数値が3~4の国(つまりGDPが1000ドル~1万ドルの国)ではジニ係数が50や60を越える国が現れて
不平等が拡大する国が多いことを示しています。
(社会騒乱多発の警戒ラインは、40であるといわれている。)
これがGDPの対数値が4を越える国(1万ドルを越える国)になると、ジニ係数が50を越える国は姿を消し、
30前後の国が大半を占めるようになります(ノルウェー25.8、スウェーデン25、日本24.9、イギリス36、アメリカ40.8など)。
経済発展の初期には農業部門から工業部門に資金が移動して格差が拡大する一方、経済発展によって
中間層が増えてくると所得再分配が行われるようになって格差が縮小する現象は、1971年にノーベル経済学賞を受賞した
サイモン・クズネッツが発見しました。そのため、この上に凸の逆U字曲線はクズネッツ曲線と呼ばれているものです。
つまり、前のブログ記事では、横軸を経済発展、縦軸に環境汚染をとった “環境クズネッツ曲線” でしたが、
縦軸に 「ジニ係数」 を取って現した関係と同じ傾向にあるというのですね。
このジニ係数は、1936年に ローレンツ曲線 をもとに、イタリアの統計学者 コッラド・ジニ によって発表されたもの
だそうです。
そしてこの係数は、所得分配の不平等さ以外にも、富の偏在性やエネルギー消費における不平等さなどにも応用されるとか。
それで、“ローレンツ曲線”とは何か? 気になりますね。
ネットに、富山大学経済学部教授 中村和之氏の論文(記事)に 分かり易い説明がありましたので、
若干割愛しながら、以下に引用させていただきました。
<中村教授(富山大学経済学部)解説より>
図 ローレンツ曲線

図で、世帯を所得の低い順番に並べ、横軸に世帯の累積比をとり、縦軸に所得の累積比をとって、世帯間の
所得分布をグラフ化したものです。 もし、社会に所得格差が存在せず、全ての世帯の所得が同額であるならば、
ローレンツ曲線は45度線と一致します。所得や富の分布に偏りがある限り、ローレンツ曲線は下方に膨らんだ形になります。
表1は平成14年の家計調査から得た標準世帯(勤労者)の年間収入階級別五分位データです。
表1 平成14年家計調査から

このデータをもとに、世帯の累積比と所得(年間収入)の累積比を求めると表2のようになります。
表2 上データの累積比

これから、世帯のローレンツ曲線を求めると下図のようになります。
図 世帯のローレンツ曲線

次に、ジニ係数ですが、ジニ係数は、ローレンツ曲線の下方への膨らみ具合を、下図のように45度線と
ローレンツ曲線にはさまれた部分の面積と45度線の下の三角形の面積の比で表します。
図の黄色い三角形の面積は必ず1/2ですから、ジニ係数は弓形の部分を2倍した値になります。
図 ローレンツ曲線とジニ係数の関係
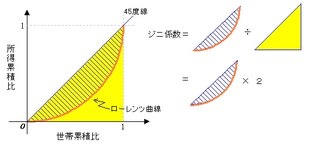
ジニ係数の値は0と1の間をとります。
その定義から明らかなように、ジニ係数の値が0に近ければ所得格差が小さく、1に近いと所得格差は大きいと言えます。
ところで、このローレンツ曲線やジニ係数の意味について考えてみます。
今、人々の生活水準(効用)が所得に依存するものとし、さらに、所得と効用の関係が下図のような形で表されるものとします。
すなわち、所得が増えると効用は上昇するが、所得が二倍になっても効用の上昇は二倍未満にとどまるものとする。
図 所得と効用
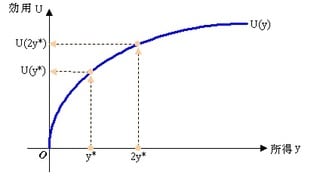
ここで、社会全体の福祉の水準(経済厚生)をW で表わし、これが人々の効用の和として表されるとすれば、
例えばN 世帯からなる社会全体の経済厚生は、
W =U(y1)+U(y2)+、…、+U(yN)、
と表すことができます。
このとき、もしも平均所得が同じであるならば、ローレンツ曲線がより45度線に近い所得分布(但し、図のように
2つのローレンツ曲線が交差しない場合だけを考えます)の方が、必ず社会全体の経済厚生(W )は大きい
ということになります。
たとえば、平均所得が同じである下図のようなふたつのローレンツ曲線によって表される所得分布があると、
ローレンツ曲線A で表される分布の方が、必ず経済厚生は大きくなります。
図 経済厚生の比較

以上は、簡単な条件下でのモデルを論じたものですが、実際には、同じ所得階層の中に異なる属性を持った世帯が
混在していますから、世帯間の属性の相違をコントロールせずにローレンツ曲線やジニ係数を測ると、
得られた結果にはみせかけの所得格差が含まれることに注意が必要です。
第二に、ジニ係数の値だけから所得格差の実態がすべて明らかになるわけではありません。
2つのローレンツ曲線が交差している場合などは、ジニ係数の値だけからこの2つの分布について優劣を下すことはできません。
第三に、社会全体の経済厚生は、所得の分配と共に、分配される所得の大きさにも依存します。
たとえば、パイの分け方とパイの大きさの双方が、社会全体の厚生水準を決めます。
平均所得は高いが格差の大きな社会と、格差は小さいが全体に貧しい社会のどちらが望ましいかについて、
ローレンツ曲線やジニ係数だけから判断を下すことはできません。
う~ん! ずいぶん勉強しましたね。
最後に、
“私たちは、経済活動の成果がどのように分配されているかと共に、これが政府によってどのように修正されているか
についても大きな関心を持っています。 政府は、社会において生ずる所得の分配が望ましくないと判断されるとき、
税制や社会保障制度を通じてこれを修正します。このことを政府による所得再分配と言います。”
お疲れさまでした。 
音楽を聴いて頭を休めてください。
もっと頭を休めたいと人はFrancis Goyaのギター演奏をどうぞ mak
<!-- Francis Goya -->















