正方形を 三等分する 関数？

前回の問題

 次のような図で、点C の座標は（１２，１２）であった。

正方形AODCの面積を２：１に分割する線BDを伸ばしたときにできる

１次関数の式をもとめましょう。

 

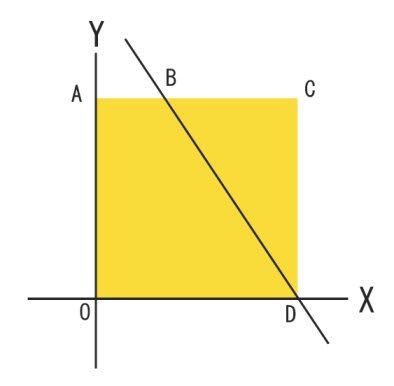
この正方形を三等分する線分の考え方は、

次の図のように まず六等分すれば分かりやすいと思います。

ACとAOを 三等分した点（B、P、Q、R）とDを結ぶ時

ここに出てきました三角形は、どれも同じ面積になります。

これで 辺BDは、正方形を４：２＝２：１ に 分割しています。

ということで、点Bの座標は （４、１２）

点B（４、１２）  と 点D（１２、０） を 結ぶ線の関数は

Y=aX+b   の X と Y に それぞれの座標のX、Y を代入して

連立方程式を作ります。

１２＝a×４＋ｂ

０＝a×１２＋ｂ

これを解いて  a＝－３／２、  ｂ＝１８

関数の式は、

Y=－３／２X＋１８

 

一見難しそうに見える 正方形の三分割ですが

補助線があれば、簡単に分かってしまいます。

そういえば以前、こんな問題があったのを覚えていますか？

一辺が１０ｃｍの正方形ABCDで、各辺の中点をEFGHとし

次のように線を引いたとき 真ん中にできる黄色い正方形の

面積はいくらになるか？

これも補助線を引くとすぐ分かりましたね～

５月１７日、５月１８日 の記事をご参照ください。

 

図形と １次関数と 座標の 問題 どうする？

 座標の中に 図形が出てくる問題は数ありますが、

次のような問題は、どうやって考えたらいいのでしょうか？

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

次のような図で、点C の座標は（１２，１２）であった。

正方形AODCの面積を２：１に分割する線BDを伸ばしたときにできる

１次関数の式をもとめましょう。




ヒント：まず、点B と 点D の 座標を求めることが大事です。

        点D は 分かるけど、点Bは どうやって求めるのか？

        そこなんですね～


---------------------------------------------------------------

前回の問題

地震発生後 A町ではP波がきて１２秒後にS波がきました。

A町にS波がきた時刻にB町ではP波がきました。

B町から震源地までの距離はいくらでしょう？

P波は毎秒７ｋｍ、S波は毎秒４ｋｍとします。

 

まず、地震発生後 A町にP波が来るまでにかかった時間を X秒 として

Xを求める式を作りますと

７X＝４（X＋１２）  となり、これを解いて  X=１６

A町にS波が来るのはその１２秒後ですから

B町にS波がくるのは（１６＋１２＝２８）より ２８秒後

震源地からB町までの距離は ７×２８＝１９６ で  １９６ｋｍ と分かります。

１次関数と 地震と 連立方程式

どこかで地震が発生しますと

最初に小さな揺れP波（Primary wave 第一波）と

その後に大きな揺れS波（Secondary wave 第二波）がやってきます。

厳密には、その伝わる速さが場所によって多少の違いがあるようですが

P波は毎秒７ｋｍ、S波は毎秒４ｋｍ の速さで進みます。

小さな揺れが始まって１５秒後に  大きな揺れがきた場合

震源地までの距離は、何ｋｍだったのでしょうか？

 

地震が発生してから小さな揺れを感じるまでの時間をX秒

震源地までの距離をYkm として 式に書きますと

Y=７X

Y=４（X+１５）   と書けます。

これを連立方程式として解きますと、

X＝20、Y＝140     となり、

地震発生から２０秒でP波がきて、震源地までの距離は、１４０ｋｍだったと分かります。

 

それでは、次のような場合はどうやって計算しましょうか？

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

地震発生後 A町ではP波がきて１２秒後にS波がきました。

A町にS波がきた時刻にB町ではP波がきました。

B町から震源地までの距離はいくらでしょう？

P波は毎秒７ｋｍ、S波は毎秒４ｋｍとします。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

この問題は、かなり現実的な問題です。

地震という波の伝わり方グラフの見方も、しっかり覚えましょうね！

（このグラフは、先ほどの問題とは無関係です。念のため）

１次関数が 回転したら どうなる～続き～～

前回の問題、１次関数が  左に９０°回転したらどうなるか？

分かりやすいように  原点を通る１次関数の場合を考えますと

図のようになります。

ここで、色の付いた直角三角形は、同じ大きさの物（合同）です。

このように直角三角形を並べると、それぞれの斜辺は９０°で交差します。

これが分かると、変化の割合が、直角三角形を見ることで分かりますね。

最初の１次関数は、切片が２でしたが、９０°回転して原点を通れば

この図に描いた赤い線と同じ関数となります。

 

では、最初の１次関数と ９０°左回転して原点を通る関数（求めた赤い線）の

交点は、どのように求めるか？

連立方程式を解いていく過程は省略しましたが、

計算してみて この答えになったら正解！

ならなかったら、式のどこかで間違っているのでチェックしてください。

 

１次関数が 回転したら どうなる～～～

図形の問題では、回転 という言葉が時々出てきました。

そして、このやっかいな回転の問題は

１次関数にもあるのです！

 

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

図のような関数を、９０°左回転させたら その関数は原点を通る。

この条件を満たす関数の式を求めよ。

また、このときの回転の中心の座標を求めよ。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

ヒントは、

次の図です。

９０°左回転すると、傾きはどうなるのか？

そこが問題です！そしてそこが ツボです。

ここが分かればこの手の問題は９割は解ける！

 

さあ、考えてみましょう～