昨日、投稿しました記事がなくなっていましたので
再度投稿いたします。
何かの具合で、消えた記事が復活すればよく似た内容の物が出てくるかもしれませんが
ご容赦願います。
前回の問題は、何通りもの考え方があると思いますが
そのうち代表的な物を２つ ご紹介いたします。
まず、１つめ。
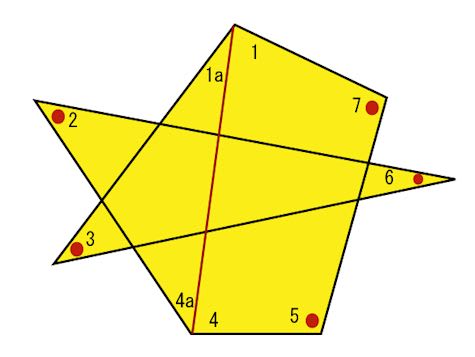
図のように、赤い補助線を入れて、１と４の角度を
分けて考えます。
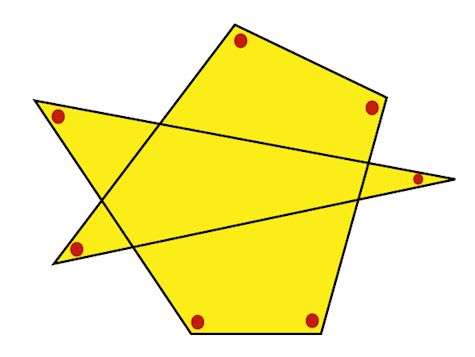
そうしますと、左側に星形の五芒星が、
右側には四角形が できます。
五芒星のとんがった角の合計は １８０°
（1aを含む小さな三角形を考えたとき
残りの二つの角は2+4a と ３＋６ で、
三角形の内角は 1a+3+6+2+4a=180)
四角形の内角の合計は３６０°（三角形が２つ分）
これらを合計しますと ５４０°です。
２つめの考え方。
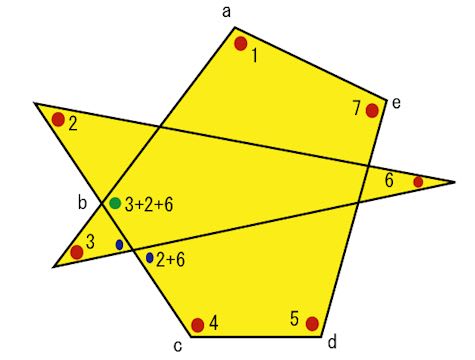
三角形の外角を考えます。
青い印の角度は、２＋６
緑の印の角度は、３＋２＋６
五角形abcdeの内角の合計は
１＋３＋２＋６＋４＋５＋７＝１８０×３＝５４０ で ５４０°
この他にもまだ解き方はあります。
自分なら、こんな風に解くな～という方法を見つけてください。
五芒星 やら 九芒星 が出てきた内角と外角の問題は
考え方が試される問題です。
今回の図形は、以前出ました問題によく似ていますが
考え方、解き方は 少し違います～
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
上の図で、赤い印のついた角の合計は、何度になるでしょう。
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
このピカチュウみたいな図で、角度の合計を求めるのですが
今回も少し工夫がいります。
解き方、考え方は ひとつではありません。
数学のおもしろいところですね。
あなたは、どの方法で解けるでしょうか？
前回の問題は、この赤い印のついた角の合計は何度？
という問題でした。
さてさて、これは何角形になるのか？って考えると
なかなか答えにたどり着きません～
そこで利用するのが、一番内側にある９角形！
赤と水色と黄色の印がついた三角形が９個ありますね
ここで、水色の印のついた角は、内側の９角形の外角です。
水色の印のついた外角は全部で９つあり、その合計は３６０°
まあ、もともと外角の合計は何角形であっても３６０°になりましたよね、
覚えてますか？
同じように黄色の印のついた角の合計も３６０°
赤と水色と黄色の印がついた三角形は９個ありましたから
その９個分の内角の和から水色の印のついた角の合計３６０°と
黄色の印のついた角の合計３６０°を引けば、
残るのは 赤い印のついた角の合計です。
式は
１８０×９－３６０－３６０＝９００ 答え９００°
別の考え方：
最初に円周を9等分しても答えは同じになるはずですから
円周を９等分し、そのうちの５つぶんの円周角を計算してもＯＫです。
3年生になったら円周角を習います。
高校入試で出たことのある問題
どこから考えたらいいのでしょうかねー
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
円周上の９つの点を下の図のように１つおきに結んだとき
図の赤い印のついた角の和を求めなさい。
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
いくつかの考え方があると思います。
図形は、創意工夫が必要！
前回の問題、2次関数と1次関数の X と Y の 変域が同じ！という場合は
その変域を長方形で囲むことができます。
これは、Xの変域が－２から６まで、
そのときのYの変域は、2次関数の式から ０から１２まで。
ここで大事なことは、2次関数の変域は最小が０であることです。
こうしてXとYの変域をグラフに長方形で書きますと
図のようにピンクの四角形になります。
1次関数のXとYの変域も これと同じということは
この変域（ピンクの長方形）の対角線になります。
1次関数 Y=ｂX＋ｃ （ｂ＞０） ですから
ｂは12/8=3/2
cは ３ だと図から分かります。
計算で求める場合は、Pの座標と Qの座標を使って
－２ｂ＋ｃ＝０
６ｂ＋ｃ＝１２
の連立方程式を解くという方法もあります。
一見むつかしそうな問題でも、考え方が分かっていると
（過去に同じ問題を解いた経験があると）
あわてずにゆっくり考えられますが、そういうノウハウがないままだと
限られた時間の中では、パニックになってしまいますよねー
