前回の問題、1次関数が 左に90°回転したらどうなるか?
分かりやすいように 原点を通る1次関数の場合を考えますと
図のようになります。
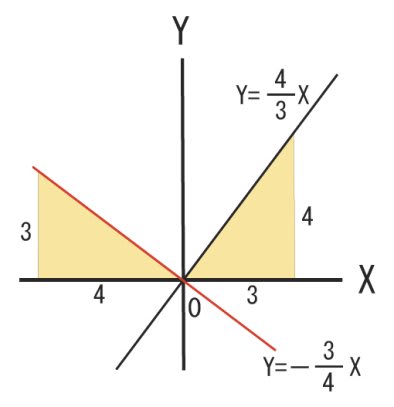
ここで、色の付いた直角三角形は、同じ大きさの物(合同)です。
このように直角三角形を並べると、それぞれの斜辺は90°で交差します。
これが分かると、変化の割合が、直角三角形を見ることで分かりますね。
最初の1次関数は、切片が2でしたが、90°回転して原点を通れば
この図に描いた赤い線と同じ関数となります。
では、最初の1次関数と 90°左回転して原点を通る関数(求めた赤い線)の
交点は、どのように求めるか?

連立方程式を解いていく過程は省略しましたが、
計算してみて この答えになったら正解!
ならなかったら、式のどこかで間違っているのでチェックしてください。









