前回の問題
回転体の体積を求めるときに、よく使うのが
円錐、円柱、球 などの 上から見ると円形の立体です。
を、くるくるっと回しますと
こんなふうになります。
この体積を求めるには、とりあえず真ん中で半分に切って
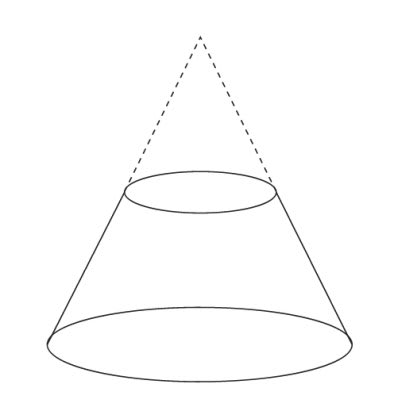こんなカタチの円錐台の 体積を考える方が
計算は、ラクになります。
これは、もともと円錐だった立体を、
高さが半分のところで水平にカットした立体です。
もともとの円錐から、カットした上の小さな円錐を引いた残りの部分です。
底面の円の半径は２ｃｍ、高さは４ｃｍですから
もともとの円錐の体積は、
カットした上の小さな円錐は、もともとの円錐と相似で、線分の比は１：２ですから
体積の比は、１の３乗：２の３乗 で、 １ ： ８
そうしますと、もともとの円錐の体積と、残った 円錐台との体積比は、８ ： ７
もともとの円錐の体積に ８分の７を掛けた物が、円錐台の体積です。
あとは、これを２倍にして、回転体の体積とします。
もう一つの問題は、次回解説します。