ビール予想(Beal's conjecture)は数学における予想で、
「もし、 かつ A,B,C,x,y,zが正の整数であり かつ x,y,z>2
かつ A,B,C,x,y,zが正の整数であり かつ x,y,z>2
ならば
A,B,Cは共通の素因数をもつ」
というものです。
フェルマーの最終定理はこれの特殊な場合(x=y=z)と言えます。(※)
Andrew Bealという大富豪が100万ドルの懸賞金をかけているそうです。
(※)ビール予想の「x=y=z」バージョンを仮定すると ちょっとした議論でフェルマーの最終定理を証明できます
ビール予想(Beal's conjecture)は数学における予想で、
「もし、 かつ A,B,C,x,y,zが正の整数であり かつ x,y,z>2
かつ A,B,C,x,y,zが正の整数であり かつ x,y,z>2
ならば
A,B,Cは共通の素因数をもつ」
というものです。
フェルマーの最終定理はこれの特殊な場合(x=y=z)と言えます。(※)
Andrew Bealという大富豪が100万ドルの懸賞金をかけているそうです。
(※)ビール予想の「x=y=z」バージョンを仮定すると ちょっとした議論でフェルマーの最終定理を証明できます
 まちカドまぞくと百合
6年前
まちカドまぞくと百合
6年前
 まちカドまぞくと百合
6年前
まちカドまぞくと百合
6年前
 まちカドまぞくと百合
6年前
まちカドまぞくと百合
6年前
 まちカドまぞくと百合
6年前
まちカドまぞくと百合
6年前
 ナシゴレン フリーイラスト
6年前
ナシゴレン フリーイラスト
6年前
 新元号「令和」と・西暦・平成の換算・早見表
6年前
新元号「令和」と・西暦・平成の換算・早見表
6年前
 新元号「令和」と・西暦・平成の換算・早見表
6年前
新元号「令和」と・西暦・平成の換算・早見表
6年前
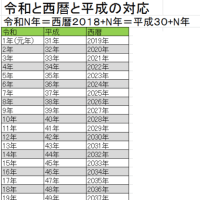 新元号「令和」と・西暦・平成の換算・早見表
6年前
新元号「令和」と・西暦・平成の換算・早見表
6年前
 ゲゲゲの鬼太郎(6期)と百合
7年前
ゲゲゲの鬼太郎(6期)と百合
7年前
 ゲゲゲの鬼太郎(6期)と百合
7年前
ゲゲゲの鬼太郎(6期)と百合
7年前
ABC予想
A^z+B^x=C^y rad(A,B,C)=D C>D^1+ε となる解の自然数(A,B,C)の
組み合わせ数は有限個であるか無限個であるか。
答えは無限個
x:y=5:4の整数比ならいつでも成立 A+2^5=3^4 C=81 A=7^2 C>D=rad(A,B,C)=42
ビール予想
2より大きい自然数のn,m,rでx^n+y^m=z^r を満たす解は存在するのか
詳細は省く
解の一例
3^6+18^3=9^4 729+5832=6561
4^12+16^6=32^5