百物語改め「九一三・六物語」

夢日記・百合・数学・怪談・神社その他

１０月３１日　ハロウィーンと命題論理学

2015-10-29 | 数学

１０月３１日はハロウィーンです。
オバケに仮装した子供たちが
「お菓子をくれないといたずらするぞ」とせびりにきます。
「お菓子をくれないといたずらするぞ」は
「trick or treat」の訳語です。
trickはいたずら、treatはおごり、ごちそう、つまりお菓子をくれることです。
直訳すると「いたずらあるいはお菓子」です。
一方、命題論理において、
AあるいはB
は　
BでないならばA
と同値です。
なので
「いたずらあるいはお菓子」を「お菓子をくれないといたずらするぞ」と
訳すのは非常に論理的なことなのです。

Aor B iff neg B to A iff neg A to B

※上記３式は同値、つまり真理関数として等しくなります。計算してみると分かります。

 

※子供たちにお菓子をあげないとどんな悪戯をされるのか気になります

 

※去年のまんがタイムきららMAXの表紙はリゼと千夜（ごちうさ）のハロウィーンコスが可愛かったです。

『まんがタイムきららMAX』

※１０月３１日は大正時代の天長節祝日でもあります。

ハロウィーンが「大正節」として現代の祝日となっていた可能性もあったかも知れません。

大正天皇の実際の誕生日は８月３１日ですが。

ちなみに命日は１２月２５日でこちらは言わずと知れたクリスマスです。

1947年までは大正天皇祭、つまりクリスマスが休日だったようです。

 


終物語ウェブサイト背景の数式

2015-10-26 | 数学

物語シリーズ、終物語のウェブサイトの背景にはうすーく数式が記述されています。

例によっていくつか解説したいと思います。

 

背景に数式がみえますが、薄くて見にくいので画像処理してみると以下のようになります。


【確率密度関数】


P(ale X le b)=int_a^b f(x)dx

 

連続な確率分布を持つ確率変数Xの確率密度関数fです。Xがある範囲に入る確率が積分によって計算されます。

【置換積分】

int_a^b f(x)dx=int_alpha^beta f(g(t))frac{dx}{dt}dt

xをx=g(t)で置換して積分します。ここにおいて、g(α)=a,g(β)=bです。

折角gという関数を導入したのですから右辺は

int_alpha^beta f(g(t))frac{dg}{dt}(t)dtとしてほしい気がします。

それにしても置換積分をするときにはライプニッツの記法の優秀さを感じます。


【極限1】

lim_{n to infty}frac{n^2}{n}=infty

極限値の計算です。

frac{n^2}{n}=nですので、n→∞で∞になるのは当然です。


【極限2】 lim_{n to infty}(2n^3-3n^2)

３乗の項が∞に発散するので全体も∞になりそうですが、正確に書くとこうなるでしょう。

lim_{n to infty}(2n^3-3n^2)=lim_{n to infty}n^3(2-frac{3}{n}) =inftycdot 2=infty

【極限3】

lim_{n to infty}frac{sqrt{n^2-1}}{n+sqrt{n^2+1}}

分母分子をnで割ります。

lim_{n to infty}frac{sqrt{n^2-1}}{n+sqrt{n^2+1}}= lim_{n to infty} frac {sqrt{1-frac{1}{n^2}}} {1+sqrt{1+frac{1}{n^2}}} =frac{1}{1+1}=frac{1}{2}

【極限3】

lim_{n to infty}sqrt{n}(sqrt{n+2}-sqrt{n})

sqrt{n+2}-sqrt{n}の部分の根号をなくすために

sqrt{n+2}+sqrt{n}をかける変形をします。

sqrt{n+2}-sqrt{n}=frac{(sqrt{n+2}-sqrt{n})(sqrt{n+2}+sqrt{n})}{sqrt{n+2}+sqrt{n}}=frac{n+2-n}{sqrt{n+2}+sqrt{n}}=frac{2}{sqrt{n+2}+sqrt{n}}よって

lim_{n to infty}sqrt{n}(sqrt{n+2}-sqrt{n}) =lim_{n to infty}frac{2sqrt{n}}{sqrt{n+2}+sqrt{n}}分母分子を√nで割って、 lim_{n to infty}frac{2}{sqrt{1+frac{2}{n}}+1} =frac{2}{sqrt{1}+1}=1


終物語（上）扉絵の数式　２

2015-10-25 | 数学

前回の記事の続きです。

終物語扉絵の数式

 


【正弦定理】

frac{a}{sinalpha}=frac{b}{sinbeta}=frac{c}{singamma}=2R

三角形の3辺をa,b,c,角をα,β,γ,外接円の半径をRとしたときに成立する式です。

余弦定理とセットで覚えるアレです。

これらの定理のため、正弦、余弦という熟語には馴染がありますが、正接（タンジェント）はなんとなく馴染がうすい。


【底の変換】

log_a b=frac{log_c b}{log_c a}

対数を他の底の対数で計算する方法です。

これによって、ある数（例えば10,e,2など）を底とする対数表を持っていればすべての対数は計算できることになります。

 

【母平均】

mu=frac{sum_{i=1}^{N}x_i}{N}

N個のデータからなる母集団の平均です。N個足し合わせてNで割るという素朴な平均です。


【標準偏差】

sigma=s=sqrt{frac{sum_{i=1}^{N}(x_i-mu)^2}{N}}

同じくN個のデータからなる母集団の標準偏差です。データがどれくらい平均μから離れているかのパラメータです。


【標本平均】

bar{x}=frac{sum_{i=1}^{n}x_i}{n}

n個のデータを取り出した平均です。取り出す元の母集団の平均μの不偏推定量になります。

すなわちbar{x}の期待値はμとなります。

 

【不偏分散の二乗根】

sigma_{bar{x}}= sqrt{frac{sum_{i=1}^{n}(x_i-bar{x})^2}{n-1}}

n個の標本抽出についての不偏分散は

sigma_{bar{x}}^2= frac{sum_{i=1}^{n}(x_i-bar{x})^2}{n-1}となります。

すなわちこの期待値は母分散σ^2となります。

ただしその二乗根sigma_{bar{x}}の期待値は母集団の標準偏差σに一致しません。

 

 


終物語（上）扉絵の数式

2015-10-24 | 数学

西尾維新の「終物語」のアニメについて、出てきた数式等を解説してきましたが、

原作の挿絵にも数式が出てくるので解説したいと思います。

第１話おうぎフォーミュラの扉絵で忍野扇ちゃんの背後の黒板の数式です。

 

【ヘロンの公式】

S_Delta =sqrt{p(p-a)(p-b)(p-c)}=pcdot r

三角形の３辺から面積を求める公式です。三角形の各辺をa,b,cとし、p=(a+b+c)/2とします。

また、rは三角形の内接円の半径です。この関係式は三辺から内接円の半径を求めるのにも使えます。


【１変数関数の微分】

f'(x)=lim_{x to 0}frac{f(x+Delta x)-f(x)}{Delta x}

１変数関数の微分の定義です。limの添え字が間違っていて正しくは

f'(x)=lim_{Delta x to 0}frac{f(x+Delta x)-f(x)}{Delta x}です。


【バーゼル問題】

sum_{n=1}^infin frac{1}{n^2} =lim_{nto infty} left( frac{1}{1^2} + frac{1}{2^2} +cdots +frac{1}{n^2} right)=frac{pi^2}{6}

１以上の整数の二乗の逆数の総和です。ゼータ関数の値ζ(2)とも言えます。すなわち

1+frac{1}{4}+frac{1}{9}+frac{1}{16}+frac{1}{25}+cdots = frac{pi^2}{6}=1.6449...です。

ぱっと見、円に関係ない式でも円周率が現れることはよくあることなのですが、ボクが初めてこの式に出会ったときは

なかなかの驚きでした。

【指数関数のべき級数展開】

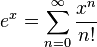
e^x=sum_{n=0}^{infty}frac{x^n}{n!}

eと底とした指数関数のべき級数展開（テイラー展開、マクローリン展開）です。

もともと指数関数なので「e^x=eをx回かけたもの」なのですが、このように展開すると複素数全体の

ある種自然な関数に拡張できます。「自然な」というのは、指数法則をみたす、連続である、複素微分可能である、などです。


【オイラーの公式】

e^{iphi}=...

式が途中で切れていますが、オイラーの公式 e^{iphi}=cosphi +isinphiでしょう。

上記e^x=sum_{n=0}^{infty}frac{x^n}{n!}のxにiφを代入すると、実部に

1-frac{phi^2}{2!}+frac{phi^4}{4!}...=cosphi

虚部に phi-frac{phi^3}{3!}+frac{phi^5}{5!}...=sinphiが現れるので公式が導かれます。

この式においてxにπを代入すると作中でも言及されるオイラーの等式

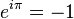e^{ipi}=-1が導かれます。

【和積の公式】

sinalpha +sinbeta=2sinfrac{alpha+beta}{2}cosfrac{alpha-beta}{2}

三角関数における和積の公式（の一つ）です。


alpha=frac{alpha+beta}{2}+frac{alpha-beta}{2},beta=frac{alpha+beta}{2}-frac{alpha-beta}{2}

であることと、sinの加法定理から導かれます。

【三角関数の相互関係】

...=frac{1}{cos^2 alpha}=sec^2 alpha

前半が切れていますが

1+tan^2alpha =frac{1}{cos^2 alpha}=sec^2 alphaでしょうか。

sec（セカント、正割）はあまりなじみがないかも知れませんが三角関数の一種でcos（余弦）の逆数です。

他にもcot（コタンジェント、余接、タンジェントの逆数）、cosec（コセカント、余割、サインの逆数）というのもあります。

斧乃木余接の名前の由来はコタンジェント（余接）かも知れません。

式の導出は三角関数の定義と三平方の定理から。

 

←アニメで「数学の妖精（？）」として登場した余接ちゃん