Adventitious right triangle problem (MIYA's 2e probleem)
S.Miyazaki (31 juli 2018)
Dit is een geavanceerde versie van 'Langley's probleem *' in elementaire geometrie.
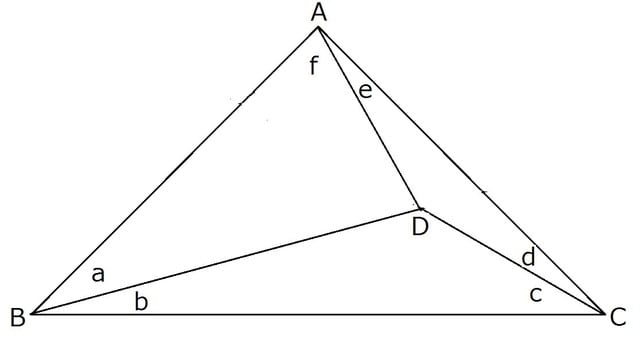
Een driehoek verdeeld in drie driehoeken binnenin wordt gekenmerkt door de hoeken a, b, c, d, e en f, zoals weergegeven in de figuur. En de driehoek verdeeld in drie driehoeken binnenin zodanig dat elke hoek gevormd door randen en diagonalen een gehele waarde in graden heeft, wordt hier "de driehoek met gehele hoek" genoemd.
Bewijs dat er slechts één "rechthoekige driehoek bestaat met integerhoeken (∠A = 90º)", en geef de waarden van integerhoeken a, b, c, d, e en f van de rechter driehoek binnen.
Hier zijn speciale gevallen van driehoeken zoals e = f = 45º (d.w.z. e + f = 90 °: rechte hoek) uitgesloten vanwege triviale oplossingen. Bovendien maken we geen onderscheid tussen de driehoek en de spiegel-symmetrische vorm / de rotatiesymmetrische vorm ervan.
(* Zie de Web Wikipedia "Langley's Adventitious Angles")
