カザフ語 Қазақ тілі, Qazaq tili, قازاق Прогрессивті үшбұрыштың проблемасы (MIYA-ның екінші мәселесі)

Прогрессивті үшбұрыштың проблемасы (MIYA-ның екінші мәселесі)
      С.Миязаки (2018 жылғы 31 шілде)
Бұл қарапайым геометриядағы «Ланглидің мәселесі» * *.
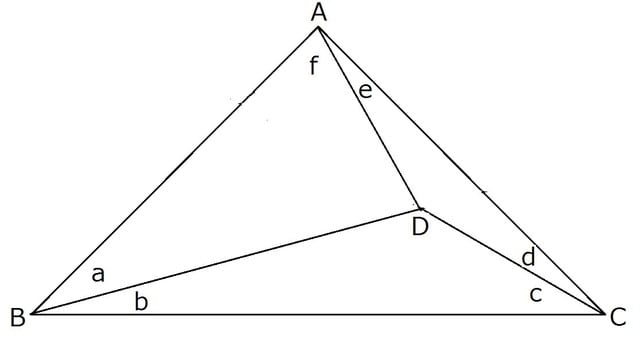
Ішкі үшбұрышқа бөлінген үшбұрыш суретте көрсетілгендей a, b, c, d, e және f бұрыштары арқылы сипатталады. Үшбұрыш үш бүйірлі үшбұрышқа бөлініп, шеттер мен диагоналдардың әр бұрышы дәрежедегі бүтіндік мәні бар, мұнда «бүтін бұрыштары бар үшбұрыш» деп аталады.
Тек бүтін бұрыштары (∠A = 90º) бар оң жақ үшбұрыш бар екенін және ішкі оң үшбұрыштың a, b, c, d, e және f бүтін бұрыштарының мәндерін келтіріңіз.
Мұнда тривиальды шешімдерге байланысты үшбұрыштың ерекше жағдайлары қарастырылады: e = f = 45º (яғни e + f = 90 °: оң жақ бұрыш). Сонымен қатар, біз үшбұрыш пен оның айналы симметрия пішіні / оның айналмалы симметрия пішіні арасында айырмашылығы жоқ.
(* «Ланглидің прогрессивті бұрыштары» атты веб-сайтты қараңыз)

オランダ語（蘭: Nederlands ) Adventitious right triangle problem (MIYA's 2e probleem)

Adventitious right triangle problem (MIYA's 2e probleem)
      S.Miyazaki (31 juli 2018)
Dit is een geavanceerde versie van 'Langley's probleem *' in elementaire geometrie.
Een driehoek verdeeld in drie driehoeken binnenin wordt gekenmerkt door de hoeken a, b, c, d, e en f, zoals weergegeven in de figuur. En de driehoek verdeeld in drie driehoeken binnenin zodanig dat elke hoek gevormd door randen en diagonalen een gehele waarde in graden heeft, wordt hier "de driehoek met gehele hoek" genoemd.
Bewijs dat er slechts één "rechthoekige driehoek bestaat met integerhoeken (∠A = 90º)", en geef de waarden van integerhoeken a, b, c, d, e en f van de rechter driehoek binnen.
Hier zijn speciale gevallen van driehoeken zoals e = f = 45º (d.w.z. e + f = 90 °: rechte hoek) uitgesloten vanwege triviale oplossingen. Bovendien maken we geen onderscheid tussen de driehoek en de spiegel-symmetrische vorm / de rotatiesymmetrische vorm ervan.
(* Zie de Web Wikipedia "Langley's Adventitious Angles")

エストニア語（eesti keel ) Juhuslik õigus kolmnurga probleem (MIYA teine probleem)

Juhuslik õigus kolmnurga probleem (MIYA teine probleem)
      S. Miyazaki (31. juuli 2018)
See on põhjalikku geomeetriat "Langley probleemi *" täiustatud versioon.
Kolmnurka, mis on jagatud kolmeks kolmnurksuks sees, iseloomustavad nurgad a, b, c, d, e ja f, nagu joonisel näidatud. Ja kolmnurk on jagatud kolmeks kolmnurksaks selliselt, et igal nurgas, mis on moodustatud servade ja diagonaalide poolest, on täisväärtus kraadis, nimetatakse siin "täisnurga kolmnurgaks".
Tõestada, et eksisteerib ainult üks "täisnurga täisnurk (∠ A = 90 º)" ja annab õige kolmnurga täisnurga a, b, c, d, e ja f väärtused.
Siinkohal jätame triviaalsete lahenduste tõttu erakorralised kolmnurgad, näiteks e = f = 45 ° (st e + f = 90 °: täisnurk). Lisaks ei erista me kolmnurka ja selle peegelsümmeetria kuju / selle pöörleva sümmeetria kuju.
(* Vaadake veebi Wikipedia "Langley's juhuslikud nurgad")

リトアニア語（ lietuvių kalba）Atsitiktinė dešinioji trikampio problema (MIYA 2-oji problema)

Atsitiktinė dešinioji trikampio problema (MIYA 2-oji problema)
      S. Miyazaki (2018 m. Liepos 31 d.)
Tai yra išplėstinė "Langley problemos *" versija elementinėje geometrijoje.
Trikampis, padalytas į tris trikampius viduje, būdingas kampais a, b, c, d, e ir f, kaip parodyta paveikslėlyje. Ir trikampis suskirstytas į tris trikampius viduje taip, kad kiekvienas kampas, suformuotas kraštais ir įstrižais, turi sveika reikšmę laipsnyje, vadinamas čia "trikampis su sveiku kampu".
Įrodykite, kad yra tik vienas "dešinys trikampis su sveiku kampu (∠ A = 90º)" ir pateikite dešinio trikampio viduje esančių sveikųjų kampų a, b, c, d, e ir f reikšmes.
Čia neįtraukiami specialūs trikampių atvejai, tokie kaip e = f = 45º (t.y., e + f = 90 °: stačiu kampu) dėl trivialių sprendimų. Be to, mes neatsižvelgiame į trikampį ir jo veidrodinės simetrijos formą / jos sukimosi simetrijos formą.
(* Žr. "Wikipedia" "Langley's Adventitious Angles")

ラトビア語、レット語（ Latviešu valoda）Adventitu right triangle problem (MIY 2. problēma)

Adventitu right triangle problem (MIY 2. problēma)
      S. Miyazaki (2018. gada 31. jūlijs)
Šī ir uzlabota versija "Langley problēma *" elementārajā ģeometrijā.
Trijstūrim, kas iedalīts trijos iekšējos trīsstūros, raksturīgi leņķi a, b, c, d, e un f, kā parādīts attēlā. Un trīsstūris iedalās trīs trīsstūros iekšpusē tādā veidā, ka katram leņķim, ko veido malas un diagonāles, ir vesels skaitlis grādos, šeit sauc par "trīsstūri ar veseliem leņķiem".
Pierādiet, ka pastāv tikai viens "labais trīsstūris ar veseliem skaitļiem" (∠ A = 90 °) "un dod iekšējā taisnā trīsstūra skaitļu a, b, c, d, e un f vērtību vērtības.
Šeit mēs izslēdzam īpašus trijstūra gadījumus, piemēram, e = f = 45º (t.i., e + f = 90 °: taisnā leņķī) triviālo šķīdumu dēļ. Turklāt mēs nenošķirim trijstūri un tā spoguļa simetrijas formu / tā rotācijas simetrijas formu.
(* Skat. Web Wikipedia "Langley's Adventitious Angles")