Atsitiktinė dešinioji trikampio problema (MIYA 2-oji problema)
S. Miyazaki (2018 m. Liepos 31 d.)
Tai yra išplėstinė "Langley problemos *" versija elementinėje geometrijoje.
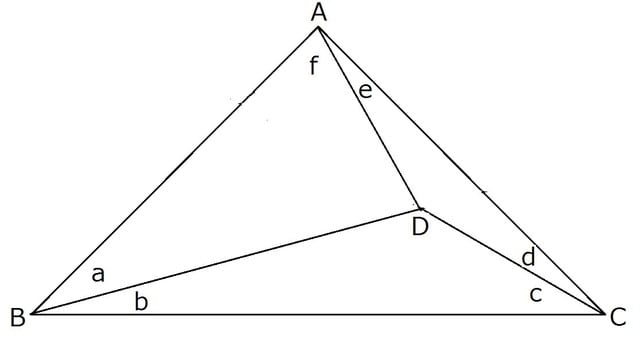
Trikampis, padalytas į tris trikampius viduje, būdingas kampais a, b, c, d, e ir f, kaip parodyta paveikslėlyje. Ir trikampis suskirstytas į tris trikampius viduje taip, kad kiekvienas kampas, suformuotas kraštais ir įstrižais, turi sveika reikšmę laipsnyje, vadinamas čia "trikampis su sveiku kampu".
Įrodykite, kad yra tik vienas "dešinys trikampis su sveiku kampu (∠ A = 90º)" ir pateikite dešinio trikampio viduje esančių sveikųjų kampų a, b, c, d, e ir f reikšmes.
Čia neįtraukiami specialūs trikampių atvejai, tokie kaip e = f = 45º (t.y., e + f = 90 °: stačiu kampu) dėl trivialių sprendimų. Be to, mes neatsižvelgiame į trikampį ir jo veidrodinės simetrijos formą / jos sukimosi simetrijos formą.
(* Žr. "Wikipedia" "Langley's Adventitious Angles")
