最初にexecuseしておくと、ボクは数学は苦手かつ趣味程度なので以下、よくわかってない可能性が高い。
選択公理は直感に反さないだろいい加減にしろ!
というページが有って大変興味深く読んだ。
さらに壱大整域さん(名前がわからん?)選択公理 選択公理と同値な命題とその証明
というページをつくっていて、これまたいろいろ集めたな~と。
選択公理というととても自明なものに見えるが、公理ということで、示すことはできないことが知られている。
そしてこれがないと様々なことが示せない。たとえば、
∪∩の分配法則
とか
線形空間における基底の存在
とか、
実数関数の連続性
とか、
可算個の可算集合の和集合は可算集合
とか
一見当たり前のようにみえることも、選択公理を認めなければ示せない(実はこれらの命題は同値である)。
また、Zornの補題とかTychonoffの定理とか、わかりにくい命題たちも同値である。
個人的には、よくある定義より、壱大整域さんが提示していた
選択公理 任意の集合は選択関数を持つ.
という定義はとても納得しやすいと思う。昔教科書で読んだ
選択公理とは「 { Xλ }λ∈Λを空でない集合からなる族とすれば、直積 Πλ∈ΛXλも空でない」という定義は
自明すぎてなんでそんなんが公理やネンと理解できず長年イラッとしつづけていた。
実数関数の連続性の証明に選択公理を使うところ、
「Xn := { y∈R | |x-y|<1/n かつ |f(x)-f(y)|≧ε } と置けば Xn≠∅ である.よって選択公理により(xn)n=1∞∈Πn=1∞Xn が取れる」
のようにexplicitにすると、ありがたみが分かってよい。
ということで自分でも選択公理が無い世界は考えづらいのだが、選択公理無しでどこまで行けるかも研究されている。
選択公理は直感に反さないだろいい加減にしろ!
というページが有って大変興味深く読んだ。
さらに壱大整域さん(名前がわからん?)選択公理 選択公理と同値な命題とその証明
というページをつくっていて、これまたいろいろ集めたな~と。
選択公理というととても自明なものに見えるが、公理ということで、示すことはできないことが知られている。
そしてこれがないと様々なことが示せない。たとえば、
∪∩の分配法則
とか
線形空間における基底の存在
とか、
実数関数の連続性
とか、
可算個の可算集合の和集合は可算集合
とか
一見当たり前のようにみえることも、選択公理を認めなければ示せない(実はこれらの命題は同値である)。
また、Zornの補題とかTychonoffの定理とか、わかりにくい命題たちも同値である。
個人的には、よくある定義より、壱大整域さんが提示していた
選択公理 任意の集合は選択関数を持つ.
という定義はとても納得しやすいと思う。昔教科書で読んだ
選択公理とは「 { Xλ }λ∈Λを空でない集合からなる族とすれば、直積 Πλ∈ΛXλも空でない」という定義は
自明すぎてなんでそんなんが公理やネンと理解できず長年イラッとしつづけていた。
実数関数の連続性の証明に選択公理を使うところ、
「Xn := { y∈R | |x-y|<1/n かつ |f(x)-f(y)|≧ε } と置けば Xn≠∅ である.よって選択公理により(xn)n=1∞∈Πn=1∞Xn が取れる」
のようにexplicitにすると、ありがたみが分かってよい。
ということで自分でも選択公理が無い世界は考えづらいのだが、選択公理無しでどこまで行けるかも研究されている。











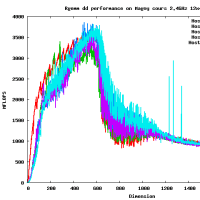

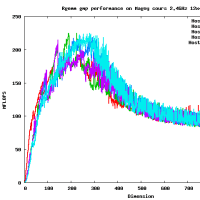
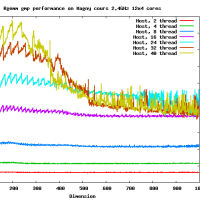
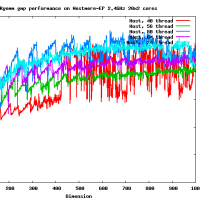
※コメント投稿者のブログIDはブログ作成者のみに通知されます