カリストの高速移行のためのガリレオ衛星の動的履歴
2022年 10月 2日提出
概要
最も内側のガリレオ衛星 (イオ、エウロパ、ガニメデ) のダイナミクスは、一連の平均運動によって特徴付けられます。
ラプラス共鳴と呼ばれる共鳴、および長半径の大きな変動を引き起こす強い潮汐散逸によって
大きなタイムスケール。木星系におけるエネルギー散逸の正確な歴史はわかっていませんが、いくつかの理論が確立されています。
提案した。潮汐共鳴ロックは、大きな外側の衛星も速く移動できることを示しています。これが Callisto のケースである場合は、
過去に 2:1 の平均運動共鳴をガニメデと交差させ、4 つのガリレオ衛星すべての運動に影響を与えました。
したがって、カリストの高速移行が現在のカリストの軌道構成と互換性があるかどうかを判断することを目指しています。
システム。共鳴交差の混沌とした性質により、さまざまな結果が生じる可能性があります。シミュレーションのごく一部
カリストは、捕獲されずにラプラス共鳴を維持することなく、ガニメデとの 2:1 共鳴を越えることができることを示しています。
ただし、ほとんどの場合、発散移動にもかかわらず、カリストは共鳴に取り込まれていることがわかりました。カリストが続けるように
高速で外側に移動するため、衛星は正確な 8:4:2:1 の通約性から大幅に逸脱しますが、それでも
レゾナントチェーン。カリストは最終的にガニメデと高次の平均運動共鳴を交差させることでそれを逃れることができます。その後、
衛星系は、衛星の適切な散逸パラメータのために現在の構成に緩和することができます。したがって、
困難ではありますが、ガリレオ衛星の過去の歴史の一貫した全体像を構築して、カリストの迅速な移行を実現することは可能です。
キーワード: 天体力学 – 惑星と衛星: 動的進化と安定性

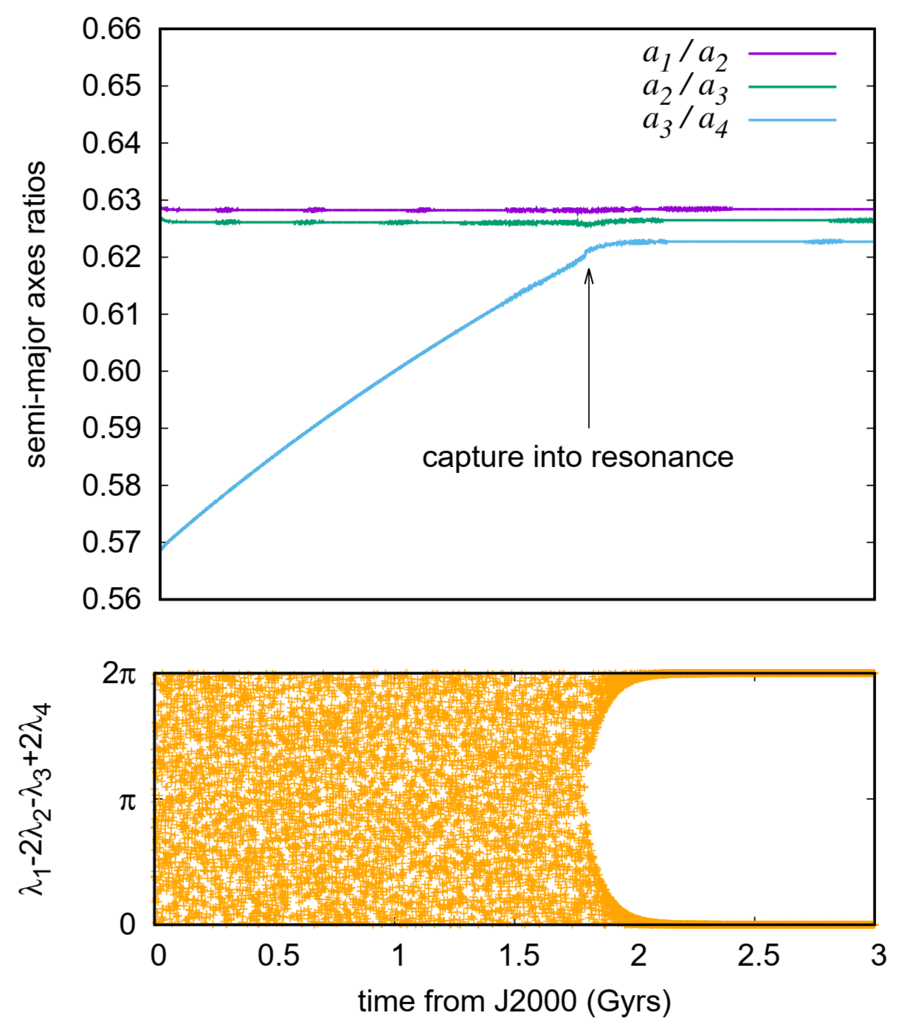
図 1. Lari らによって記述されたガリレオ衛星の将来の進化。
(2020)、カリストの距離での潮の影響は無視できると仮定しています。
J2000 エポックから約 1.5 Gyr 後、カリストは 4 つのボディに取り込まれます。
イオ、エウロパ、ガニメデとの共鳴鎖。

図 2. 周波数における木星の実効散逸パラメータの値
カリスト (푘2/푄)0,4 は、カリストの長半径 푎4 の関数として、
共振的にロックされていること。 現在の 푎4 の値は約 26.4 푅J です。
. 色付き
曲線は、式を使用して取得されます。 (16) パラメータ 퐵 の値が異なる場合。
黒い破線の曲線は、考慮された (푘2/푄)0,4 の値の変化を示しています。
ダウニーらで。 (2020) 彼らのシミュレーションのために。

図 3. ケース A の軌道進化の例: カリストが
共鳴し、ラプラス角は自由に動き続けます。 左の列は
カリストがガニメデと 2:1 MMR をトリガーするシミュレーション (サブケース)
A.1)。 右の列は、Callisto が純粋な
エウロパとガニメデ (サブケース A.2) を含む 3 体 MMR (式 18)。 の
両方のシミュレーションで、퐵 = 1.5 および (푘2/푄)푖 = 0.005 (푖 = 2, 3, 4) に設定します。
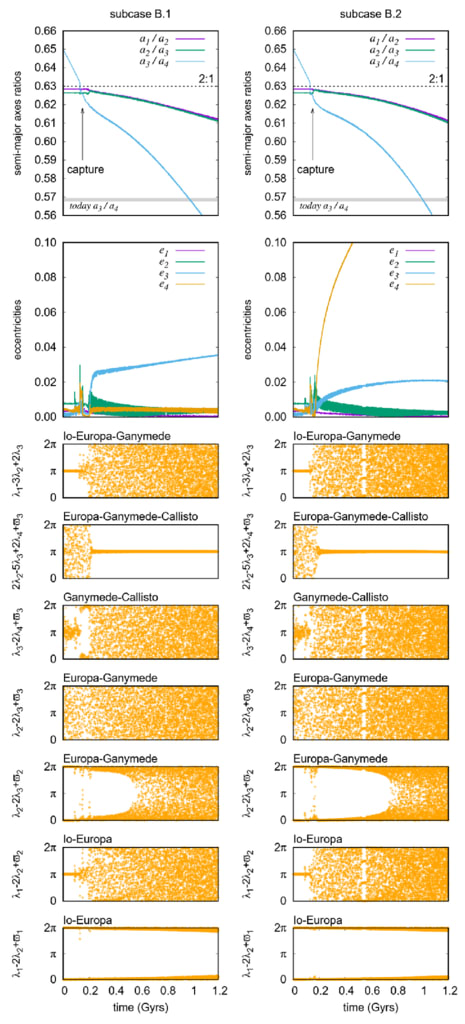
図 4. ケース B の軌道進化の例: カリストが捕獲される
共鳴し、ラプラス角が循環し始めます。 左の列
離心率の主な増加がガニメデであるシミュレーションを示します
(サブケース B.1)。 右の列は、主に増加するシミュレーションを示しています。
離心率 は カリスト 用です (サブケース B.2)。 両方のシミュレーションで、B = 1.5 および (k2/Q)i = 0.005 (i = 2, 3, 4)を設定します。
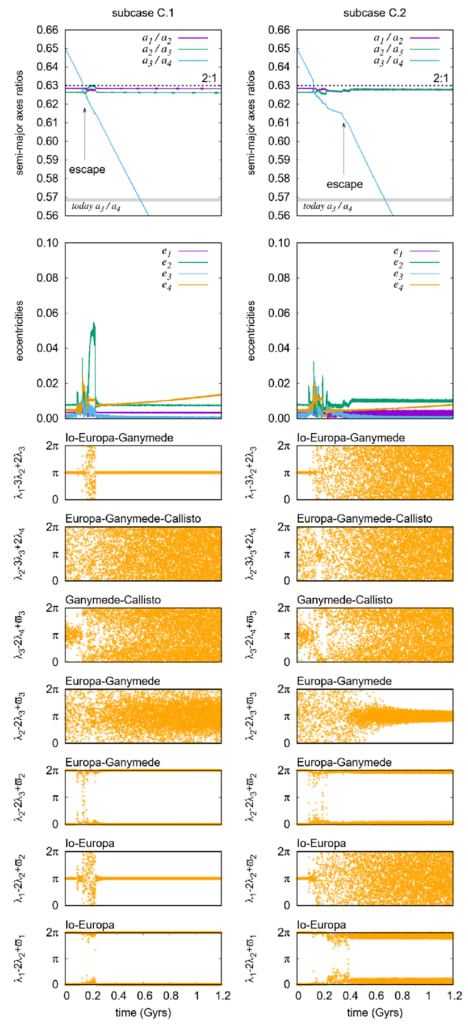
図 5. ケース C の軌道進化: カリストは共鳴に取り込まれません。 左の列は、ラプラス共鳴が
保存されます (サブケース C.1)。 右の列は、
ラプラス共鳴が中断されます (サブケース C.2)。 両方のシミュレーションで、
B = 1.5 および (k2/Q)i = 0.001 (i = 2, 3, 4)がセットされます。
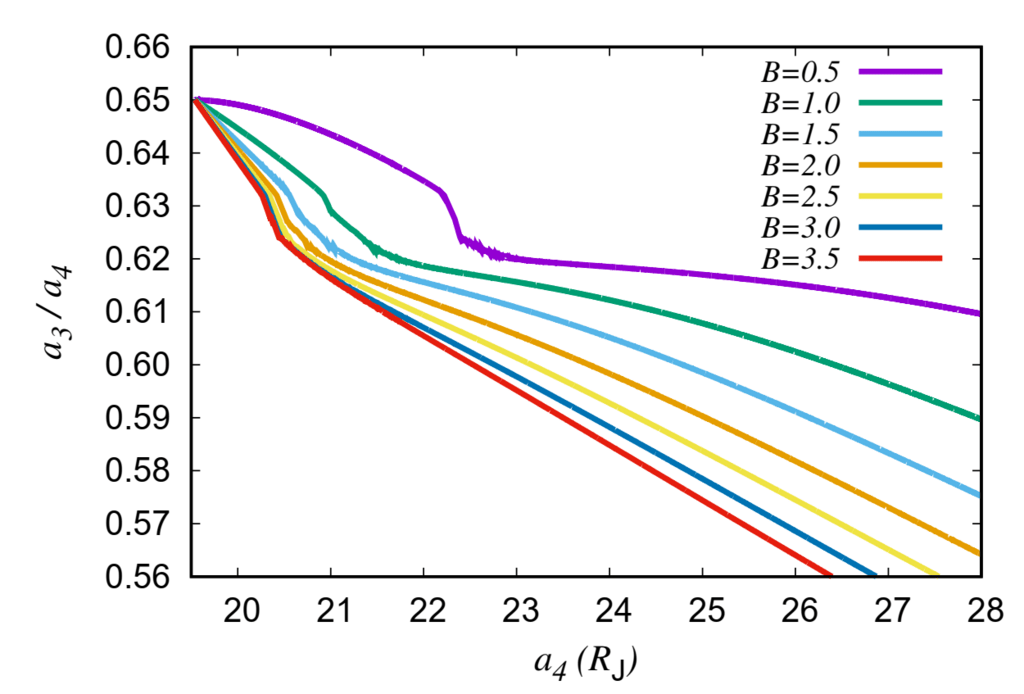
図 6. 長半径比 a3/a4 の進化 a4の関数の結果 A、表 2 の初期条件 III から開始し、さまざまな条件を使用
潮汐パラメーターBの値。 Bのほうがシステムの進化が早い
より大きい: 示されている進化は、B = 3.5 および 2.0 Gyrs に対して約 0.3 Gyrs かかります
B = 0.5 の場合。
5。結論
Fuller らの潮汐共鳴ロック理論。 (2016) と
レイニーらによって測定されたタイタンの高速移動。 (2020) 新規オープン
太陽系のダイナミクスを理解する上での道。あ
木星周辺のカリストの高速移動も提案されています
(Fuller et al. 2016)、しかし、この仮説が成り立つかどうかは不明でした。
の現在の独特の構成と一致するかどうか
ガリレオ衛星システム。の効果に関する予備調査
ダウニーらによって Callisto の迅速な移行が行われました。
(2020)。彼らは、Callisto が他のものよりも速く移行する場合、
であれば、ガニメデとの 2:1 MMR を超えているはずです。
過去に。ただし、その結果は桁違いに限られています
推定、およびこれの可能な結果の統計分析
混沌としたイベントはまだありませんでした。ここでは、過去の軌道を探索しました
数値積分によるガリレオ衛星のダイナミクス
そして、カリストの急速な移行がもたらす可能性のある影響を分類しました。として
共鳴交差イベントはごく最近のものであると予想されます。
3 つの内側の月の間のラプラス共鳴を想定
当時すでに確立されていました。これはフォーメーションと一致しています。
ラプラス共鳴の原始起源を予測するモデル (参照
Peale & Lee 2002)。
カリストとガニメデの共鳴する出会いは、
混沌としている場合、システムがたどった可能性のある動的経路を確実に知ることはできないため、統計分析を行う必要があります
可能な結果。この目的のために、平均化された
の近くで有効なガリレオ衛星のモデル
2:1共鳴。これにより、数百回のシミュレーションを
適度な時間。カリストが橋を渡れることが分かった
ラプラス共鳴は捕獲されることなく共鳴することができます
一時的な励起のみで、このイベント中に保存されます。
衛星の偏心。ただし、この結果はほんの一部にすぎません
可能な軌道の割合 (約 2%)。
ほとんどの場合、カリストは共鳴に取り込まれます
その多様な移行にもかかわらず。これは、カリストが通過するときに発生します
ガニメデとの 2:1 の通約性を取り囲む 3 体 MMR のジャングルを通り抜けます。したがって、カリストの捕獲は、
4 つのガリレオ衛星すべてを含む共鳴チェーン。これから
つまり、Callisto の迅速な移行が主な推進力になります。
カリストが木星から獲得した角運動量が 4 つの衛星すべてに再分配されるため、衛星の移動が行われます。この強い
しかし、カリストの外向きの引力は永遠に続くことはできません。
隣接する衛星の各ペアは、徐々に離れてドリフトします。
正確な 2:1 の通約性。このドリフトプロセスを調査しました
非平均数値シミュレーション。私たちのシミュレーションは、
衛星は 3 体 MMR に閉じ込められたままで、カリストは交差します。
ガニメデとの高次二体 MMR (例: 7:3、9:4、11:5...)。
その時の衛星の離心率の値によっては、
最終的な共鳴交叉は、数億年後にカリストを共鳴鎖から解放することができます。したがって、まだ取得する可能性があります
現在のガリレオに質的に似た構成
カリストが一時的に捕獲されたとしても衛星。それでも、私たちのシミュレーションは
この場合、今日のデータをすべて取得するのは難しいことを示しています。
共振関係、長半径比、および衛星の離心率。
ガニメデの離心率が大きな値になると (
潮の散逸があれば、シミュレーションの 9% で起こる
ガニメデ内は十分に低い)、カリストはガニメデから早く脱出する
共鳴チェーンとそれは現在の場所に移動することができます
ラプラス共鳴は観測された状態に緩和します。この状況では、
Callisto は現在も急速に移行している可能性があります。代わりに、偏心
の衛星が非常に低いままである場合 (シミュレーションの 78% で発生)、カリストは共鳴チェーンから遅れて脱出し、
現在の比率 a3/a4 を超えた後。この 2 番目の状況では、Callisto の急速な移行は、必然的にどこかで停止したに違いありません。
他の 3 つのガリレオ衛星が追いついて復元できるように
現在の比率 a3/a4.これらの 2 つの状況は、混沌とした共鳴の遭遇の結果として発生する可能性がありますが、罰金が必要です。
衛星の散逸パラメータの調整
比率 a3/a4 までに現在の離心率を取得する
現在の値に到達します。
衛星の離心率の一時的な増加は、
これらの異なる経路を区別する方法。特に、ガニメデの離心率は 0.06 まで大きくなる可能性があり、これは
その結果、衛星内に強い潮汐摩擦が生じます。この強化された
内部の熱は地殻変動の再浮上の原因となる可能性があり、
ガニメデの表面の滑らかな明るい地形 (Malhotra 1991;
ショーマン & マルホトラ 1997;シューベルト等。 2004)。
木星系における潮汐散逸に関する現在の知識は、衛星の天体観測から得られたものであり、
イオ内の強い散逸を見積もるため (Lainey et al. 2009)、
観測された熱流の主な原因です (Veeder et al. 1994)。
ただし、利用可能なデータセットに制限があるため、
に関連する散逸パラメータの正確な推定値を持っていません。
他の月。近い将来、JUICEとエウロパクリッパー宇宙
ミッションは木星系を訪れ、複数回のフライバイを行います
ガリレオ衛星。彼らは重要な観察を提供します
木星のエネルギー散逸をさらに調査することができます
システム (Dirkx et al. 2017; Lari & Milani 2019)。特に、
宇宙ミッションからの正確な電波科学と
より広い範囲をカバーする他のデータセット (天体観測など)
タイムスパン、散逸パラメータを推定することが可能である可能性があります
4 つのガリレオ衛星すべてと、異なる軌道にある木星の衛星の周波数。このようにして、可能になるだけでなく
イオ内の強い潮汐消散を確認するだけでなく、他の衛星内の潮汐摩擦に関する情報。最も重要なことは、これらの将来の観察がカリストの証拠を示す可能性があることです。
木星内で行われている移行と散逸プロセス。
この記事全体を通して、私たちの作業仮説は、Fuller らによって提案された Callisto の仮説的な高速移行でした。 (2016)。まだ、
たとえ将来の測定で Callisto の移行が
今日は遅かったが、私たちの結果は、過去には速かったかもしれないことを示している
それでもシステムの現在の構成につながります。実際、
4 つのガリレオ衛星すべての力学的進化は深く結合されており、
そのため、すべての散逸パラメータの知識が不可欠です
軌道の歴史を再構築する
2022年 10月 2日提出
概要
最も内側のガリレオ衛星 (イオ、エウロパ、ガニメデ) のダイナミクスは、一連の平均運動によって特徴付けられます。
ラプラス共鳴と呼ばれる共鳴、および長半径の大きな変動を引き起こす強い潮汐散逸によって
大きなタイムスケール。木星系におけるエネルギー散逸の正確な歴史はわかっていませんが、いくつかの理論が確立されています。
提案した。潮汐共鳴ロックは、大きな外側の衛星も速く移動できることを示しています。これが Callisto のケースである場合は、
過去に 2:1 の平均運動共鳴をガニメデと交差させ、4 つのガリレオ衛星すべての運動に影響を与えました。
したがって、カリストの高速移行が現在のカリストの軌道構成と互換性があるかどうかを判断することを目指しています。
システム。共鳴交差の混沌とした性質により、さまざまな結果が生じる可能性があります。シミュレーションのごく一部
カリストは、捕獲されずにラプラス共鳴を維持することなく、ガニメデとの 2:1 共鳴を越えることができることを示しています。
ただし、ほとんどの場合、発散移動にもかかわらず、カリストは共鳴に取り込まれていることがわかりました。カリストが続けるように
高速で外側に移動するため、衛星は正確な 8:4:2:1 の通約性から大幅に逸脱しますが、それでも
レゾナントチェーン。カリストは最終的にガニメデと高次の平均運動共鳴を交差させることでそれを逃れることができます。その後、
衛星系は、衛星の適切な散逸パラメータのために現在の構成に緩和することができます。したがって、
困難ではありますが、ガリレオ衛星の過去の歴史の一貫した全体像を構築して、カリストの迅速な移行を実現することは可能です。
キーワード: 天体力学 – 惑星と衛星: 動的進化と安定性

図 1. Lari らによって記述されたガリレオ衛星の将来の進化。
(2020)、カリストの距離での潮の影響は無視できると仮定しています。
J2000 エポックから約 1.5 Gyr 後、カリストは 4 つのボディに取り込まれます。
イオ、エウロパ、ガニメデとの共鳴鎖。

図 2. 周波数における木星の実効散逸パラメータの値
カリスト (푘2/푄)0,4 は、カリストの長半径 푎4 の関数として、
共振的にロックされていること。 現在の 푎4 の値は約 26.4 푅J です。
. 色付き
曲線は、式を使用して取得されます。 (16) パラメータ 퐵 の値が異なる場合。
黒い破線の曲線は、考慮された (푘2/푄)0,4 の値の変化を示しています。
ダウニーらで。 (2020) 彼らのシミュレーションのために。

図 3. ケース A の軌道進化の例: カリストが
共鳴し、ラプラス角は自由に動き続けます。 左の列は
カリストがガニメデと 2:1 MMR をトリガーするシミュレーション (サブケース)
A.1)。 右の列は、Callisto が純粋な
エウロパとガニメデ (サブケース A.2) を含む 3 体 MMR (式 18)。 の
両方のシミュレーションで、퐵 = 1.5 および (푘2/푄)푖 = 0.005 (푖 = 2, 3, 4) に設定します。

図 4. ケース B の軌道進化の例: カリストが捕獲される
共鳴し、ラプラス角が循環し始めます。 左の列
離心率の主な増加がガニメデであるシミュレーションを示します
(サブケース B.1)。 右の列は、主に増加するシミュレーションを示しています。
離心率 は カリスト 用です (サブケース B.2)。 両方のシミュレーションで、B = 1.5 および (k2/Q)i = 0.005 (i = 2, 3, 4)を設定します。

図 5. ケース C の軌道進化: カリストは共鳴に取り込まれません。 左の列は、ラプラス共鳴が
保存されます (サブケース C.1)。 右の列は、
ラプラス共鳴が中断されます (サブケース C.2)。 両方のシミュレーションで、
B = 1.5 および (k2/Q)i = 0.001 (i = 2, 3, 4)がセットされます。

図 6. 長半径比 a3/a4 の進化 a4の関数の結果 A、表 2 の初期条件 III から開始し、さまざまな条件を使用
潮汐パラメーターBの値。 Bのほうがシステムの進化が早い
より大きい: 示されている進化は、B = 3.5 および 2.0 Gyrs に対して約 0.3 Gyrs かかります
B = 0.5 の場合。
5。結論
Fuller らの潮汐共鳴ロック理論。 (2016) と
レイニーらによって測定されたタイタンの高速移動。 (2020) 新規オープン
太陽系のダイナミクスを理解する上での道。あ
木星周辺のカリストの高速移動も提案されています
(Fuller et al. 2016)、しかし、この仮説が成り立つかどうかは不明でした。
の現在の独特の構成と一致するかどうか
ガリレオ衛星システム。の効果に関する予備調査
ダウニーらによって Callisto の迅速な移行が行われました。
(2020)。彼らは、Callisto が他のものよりも速く移行する場合、
であれば、ガニメデとの 2:1 MMR を超えているはずです。
過去に。ただし、その結果は桁違いに限られています
推定、およびこれの可能な結果の統計分析
混沌としたイベントはまだありませんでした。ここでは、過去の軌道を探索しました
数値積分によるガリレオ衛星のダイナミクス
そして、カリストの急速な移行がもたらす可能性のある影響を分類しました。として
共鳴交差イベントはごく最近のものであると予想されます。
3 つの内側の月の間のラプラス共鳴を想定
当時すでに確立されていました。これはフォーメーションと一致しています。
ラプラス共鳴の原始起源を予測するモデル (参照
Peale & Lee 2002)。
カリストとガニメデの共鳴する出会いは、
混沌としている場合、システムがたどった可能性のある動的経路を確実に知ることはできないため、統計分析を行う必要があります
可能な結果。この目的のために、平均化された
の近くで有効なガリレオ衛星のモデル
2:1共鳴。これにより、数百回のシミュレーションを
適度な時間。カリストが橋を渡れることが分かった
ラプラス共鳴は捕獲されることなく共鳴することができます
一時的な励起のみで、このイベント中に保存されます。
衛星の偏心。ただし、この結果はほんの一部にすぎません
可能な軌道の割合 (約 2%)。
ほとんどの場合、カリストは共鳴に取り込まれます
その多様な移行にもかかわらず。これは、カリストが通過するときに発生します
ガニメデとの 2:1 の通約性を取り囲む 3 体 MMR のジャングルを通り抜けます。したがって、カリストの捕獲は、
4 つのガリレオ衛星すべてを含む共鳴チェーン。これから
つまり、Callisto の迅速な移行が主な推進力になります。
カリストが木星から獲得した角運動量が 4 つの衛星すべてに再分配されるため、衛星の移動が行われます。この強い
しかし、カリストの外向きの引力は永遠に続くことはできません。
隣接する衛星の各ペアは、徐々に離れてドリフトします。
正確な 2:1 の通約性。このドリフトプロセスを調査しました
非平均数値シミュレーション。私たちのシミュレーションは、
衛星は 3 体 MMR に閉じ込められたままで、カリストは交差します。
ガニメデとの高次二体 MMR (例: 7:3、9:4、11:5...)。
その時の衛星の離心率の値によっては、
最終的な共鳴交叉は、数億年後にカリストを共鳴鎖から解放することができます。したがって、まだ取得する可能性があります
現在のガリレオに質的に似た構成
カリストが一時的に捕獲されたとしても衛星。それでも、私たちのシミュレーションは
この場合、今日のデータをすべて取得するのは難しいことを示しています。
共振関係、長半径比、および衛星の離心率。
ガニメデの離心率が大きな値になると (
潮の散逸があれば、シミュレーションの 9% で起こる
ガニメデ内は十分に低い)、カリストはガニメデから早く脱出する
共鳴チェーンとそれは現在の場所に移動することができます
ラプラス共鳴は観測された状態に緩和します。この状況では、
Callisto は現在も急速に移行している可能性があります。代わりに、偏心
の衛星が非常に低いままである場合 (シミュレーションの 78% で発生)、カリストは共鳴チェーンから遅れて脱出し、
現在の比率 a3/a4 を超えた後。この 2 番目の状況では、Callisto の急速な移行は、必然的にどこかで停止したに違いありません。
他の 3 つのガリレオ衛星が追いついて復元できるように
現在の比率 a3/a4.これらの 2 つの状況は、混沌とした共鳴の遭遇の結果として発生する可能性がありますが、罰金が必要です。
衛星の散逸パラメータの調整
比率 a3/a4 までに現在の離心率を取得する
現在の値に到達します。
衛星の離心率の一時的な増加は、
これらの異なる経路を区別する方法。特に、ガニメデの離心率は 0.06 まで大きくなる可能性があり、これは
その結果、衛星内に強い潮汐摩擦が生じます。この強化された
内部の熱は地殻変動の再浮上の原因となる可能性があり、
ガニメデの表面の滑らかな明るい地形 (Malhotra 1991;
ショーマン & マルホトラ 1997;シューベルト等。 2004)。
木星系における潮汐散逸に関する現在の知識は、衛星の天体観測から得られたものであり、
イオ内の強い散逸を見積もるため (Lainey et al. 2009)、
観測された熱流の主な原因です (Veeder et al. 1994)。
ただし、利用可能なデータセットに制限があるため、
に関連する散逸パラメータの正確な推定値を持っていません。
他の月。近い将来、JUICEとエウロパクリッパー宇宙
ミッションは木星系を訪れ、複数回のフライバイを行います
ガリレオ衛星。彼らは重要な観察を提供します
木星のエネルギー散逸をさらに調査することができます
システム (Dirkx et al. 2017; Lari & Milani 2019)。特に、
宇宙ミッションからの正確な電波科学と
より広い範囲をカバーする他のデータセット (天体観測など)
タイムスパン、散逸パラメータを推定することが可能である可能性があります
4 つのガリレオ衛星すべてと、異なる軌道にある木星の衛星の周波数。このようにして、可能になるだけでなく
イオ内の強い潮汐消散を確認するだけでなく、他の衛星内の潮汐摩擦に関する情報。最も重要なことは、これらの将来の観察がカリストの証拠を示す可能性があることです。
木星内で行われている移行と散逸プロセス。
この記事全体を通して、私たちの作業仮説は、Fuller らによって提案された Callisto の仮説的な高速移行でした。 (2016)。まだ、
たとえ将来の測定で Callisto の移行が
今日は遅かったが、私たちの結果は、過去には速かったかもしれないことを示している
それでもシステムの現在の構成につながります。実際、
4 つのガリレオ衛星すべての力学的進化は深く結合されており、
そのため、すべての散逸パラメータの知識が不可欠です
軌道の歴史を再構築する




















※コメント投稿者のブログIDはブログ作成者のみに通知されます