ジュノとガリレオの観測を満足する木星の新しいモデル

探査機２機の観測結果を矛盾なくつなぐ木星の内部構造モデル。以下、機械翻訳。
ジュノとガリレオの観測を満足する木星の新しいモデル
（2019年1月17日に投稿された）
ジュノによる木星の重力場の観測は、20年前にガリレオによって測定された重元素の存在量を考慮すると、高次重力モーメントの驚くほど小さい値を明らかにしました。水素とヘリウムの最近の状態方程式の導出は、Mbar地域でははるかに密度が高いため、これら2つの観測間の矛盾を悪化させます。このパズルを回避するために、現在の木星モデル研究はガリレオからの制約を無視するか、または状態方程式の特別な修正を呼び出す。本稿では、JunoとGalileoの両方の制約を満たす木星モデルを導出する。木星の構造は、少なくとも4つの異なる領域を含む必要があることを確認します。外側の対流エンベロープ、組成の領域、つまりエントロピーの変化。内部の対流エンベロープと重い元素が豊富な拡張希薄コア、そして潜在的には中央のコンパクトコア。我々は、JunoとGalileoの観測を再現するために、外部と内部の包絡線間のエントロピーの大幅な増加と、外部差動回転に伴う等エントロピープロファイルよりも小さい密度が必要であることを示します。この後者の条件を満たすための最善の方法は、この地域の重元素の内向き減少量です。エントロピーと組成のそのような変化をもたらすことができる3つの物理的メカニズムを詳細に調べます：一次分子 - 金属水素転移、水素とヘリウムの間の非混和性または層状対流の領域。我々の水素の圧力イオン化の現在の知識という条件のもとで、２つの後のメカニズムの組み合わせが最も人気がある解決であるように思われます。
キーワード：惑星と衛星：ガスの惑星 － 惑星と衛星：内部 － 惑星と衛星：構成 － 惑星と衛星：個別の（木星） － 国家の方程式

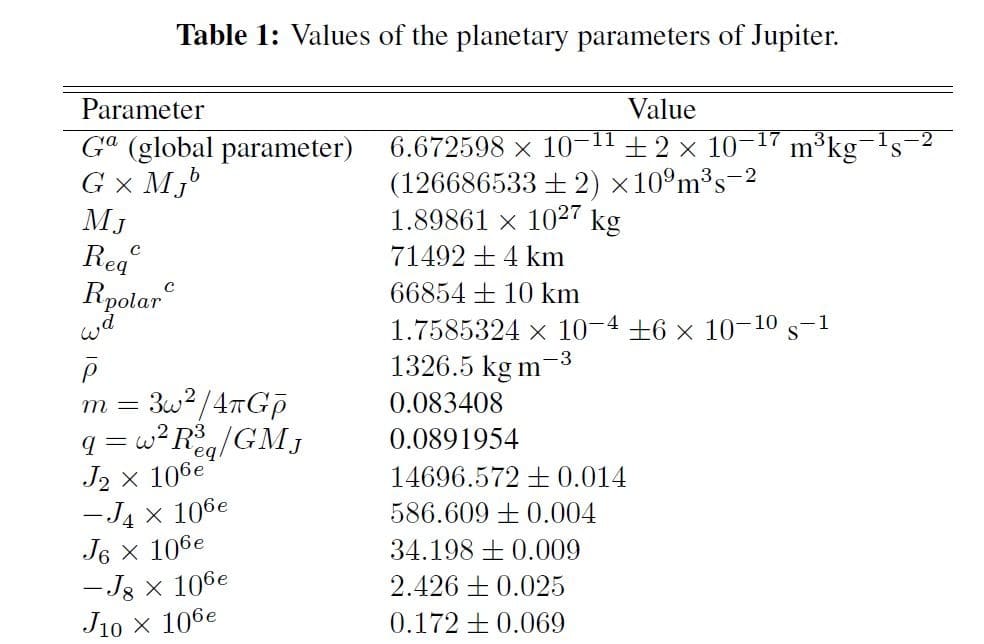
表１：木星の惑星のパラメータの値。


図１： MH13 の間の密度の上の相対的なエラーそして我々の、あるいはミゲルおよびその他. （２０１６）Ｙ ＝ ０.２４６６のための入り混ざった EOS 。


図２： J4×106 対異なったモデルのための J6×106 （テキストを見てください）とエラーバーがあまりにも小さいという状態で、この図の上に見られる Juno の値（Iess およびその他、２０１８）。 陰にされるエリアは、 Kaspi およびその他によって評価されるように、１００００キロより浅い差別的な回転から生じている graviational 瞬間に不確実に対応します。 （２０１７）。


図３：封筒（左）のあるいは（正しい）コアにおける内部エントロピー相違を持っている木星の単純な構造（§３.２.２参照）。 これらのモデルのいずれも Juno とガリレオ両方の観察と一致することができません。


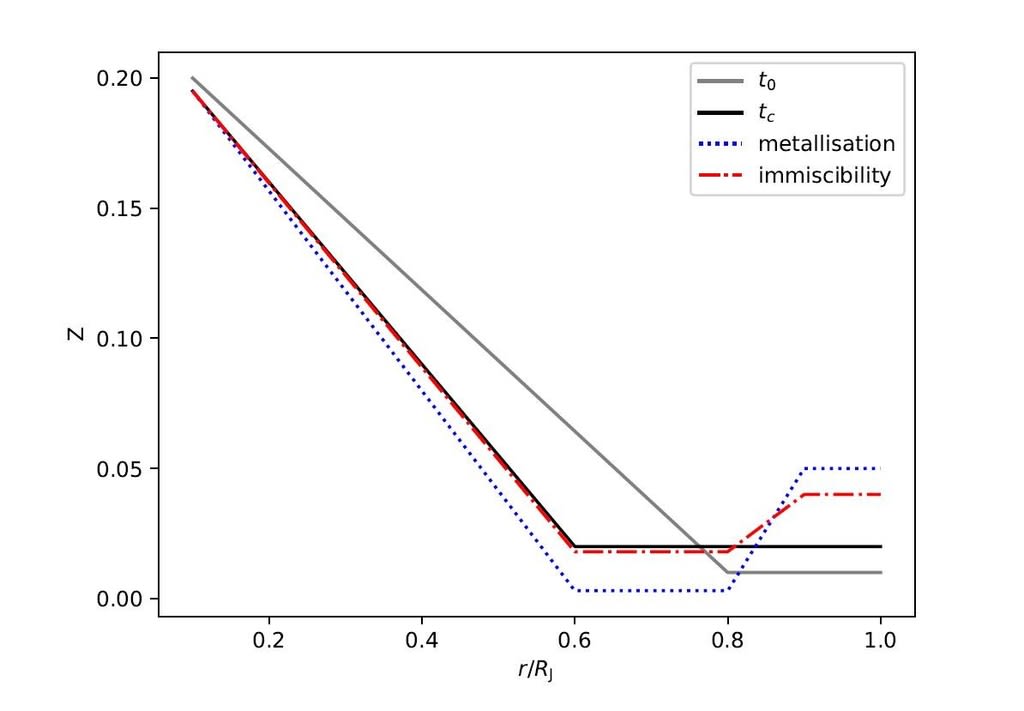
図４：ラジアル距離の機能としてのＺが、最初のオーダー段階移行（PPT）あるいは immiscibility が冷却の歴史の間に起こるであろうと想定して、時間を持っていることに満足している重い要素の典型的な進化。 ｔ ＝ t0 において木星はただできました。 小さい convective の外部の封筒が次第に薄い惑星、コア付加物から継承された構造に関係しています。 ｔ ＝ tc において、 immiscibility あるいは最初のオーダー metallisation が起きようとしています。 convective 地域は、惑星で金属内容を再配布して、いくぶん拡張しました。 後に（「metallisation」カーブ）の上に、内側の１使い果たされる間に、上昇する泡は重い要素に外の封筒を濃縮しました。 もし immiscibility が起きます（「immiscibility」カーブ）なら、内側の封筒の中のこれらの要素の希薄がほとんど取るに足りないのに対して、外の封筒は外の封筒で重い要素を大量の分数増やして、溺れかけたヘリウム dropplets のために結局はその量の一部を失うでしょう。


図５：我々の最終の木星モデルの図式の内部構造。 テキストで述べられるように Yext ＝ ０.２３、 Zext ＝ ０.０２。 (a) 外の、そして内側の封筒の間の穏当なエントロピーの増加は希薄な核心でこの後者の中ぐらいのヘリウムの増加と内部のヘリウム豊かさをもたらします（テキスト参照）。 (b) inhomogeneous boudary 範囲のより大きいエントロピーの増加は内側の封筒で supersolar ヘリウム分数をもたらします、しかしそれからヘリウム豊富は希薄な核心に関して減少します。 (c) 我々の最も少なく人気があるモデル. 内側の封筒のヘリウムと重い要素 abundances 両方の増加が、身体的に達成可能なことの限界において、強いエントロピーの増加を必要とします。 構造 (a) と（ｃ）の混合が同じく可能で、ヘリウムと重い元素両方の小さい増加にあります。 必要とされる ? Ｓは（ｂ）に相当するでしょう。


図６：我々が、 Zext の２つの値で、 Jk - Jk ＋ ２つの計画 － で種々のモデルで得る重力の期間。 例えば、ギヨおよびその他でされるように、すべての値は１つの×１０６を掛けられます。 （２０１８）。 緑の点は、どんな dynamical 訂正もなしで、観察されたエラーバー（Iess およびその他、２０１８）と共に Juno 価値です。 企てられたエリアはギヨおよびその他のモデルに対応します。 （２０１８）。


図７： (a) 寄付の引き算が共に isentropic モデルのために、圧力あるいは半径に関して、（彼・それ）らの最大限に標準化された J2 マイナスの J4 で作用します。 (b) 強いエントロピーの変化で小さいエントロピーの変化を持っているモデルとモデルの間に J8 に J2 で貢献機能の相違を正常化しました.


図８：エントロピーの機能としての優れた重力の瞬間が封筒で ? Ｓを跳び越えます。 これらすべてのモデルは Kaspi およびその他と一緒に Juno の観察から許可された限界以内に J2 と J4 値を持っています。 （２０１８）訂正、それらを除外してください
？（そのために）我々が J4 に匹敵しさえすることができなかったＳ ＝ ０。 Zext 価値は大気のＺです、「Juno」は３つのσエラーバーと共に Juno の観察に対応します、「Juno ＋ Kaspi2018」は Kaspi およびその他に推定風によって修正される観察です。
（２０１８）と「Juno ＋ Kaspi2017」が Kaspi およびその他から、３０００キロより浅い差別的な回転に帰せられる観察された重力の瞬間まで訂正を含みます。 （２０１７）。 いくつかのモデルが、 Kaspi およびその他によって見積もられた差異のために訂正を考慮に入れるとき、 Juno の観察と両立できる間に。 （２０１７）、これは、訂正が Kaspi およびその他によって奇妙な重力の瞬間から得られたと考えるとき、ずっと困難になります。 （２０１８）。 この後のケースで、 ? Ｓ ＝ ０あるいは∇Ｚ ＜ ０を持っているモデルのいずれも木星の重力の瞬間を再生させることができないことに注意を払ってください。