黒縞模様画像が記事585 で赤分岐していく様子をアニメ化した。 (参考:そのアニメ→分岐画像)
その分岐画像の途中で、赤黒縞画像の縁(ふち)とマンデルブロ集合の縁とが類似している箇所がある。
下図がその例。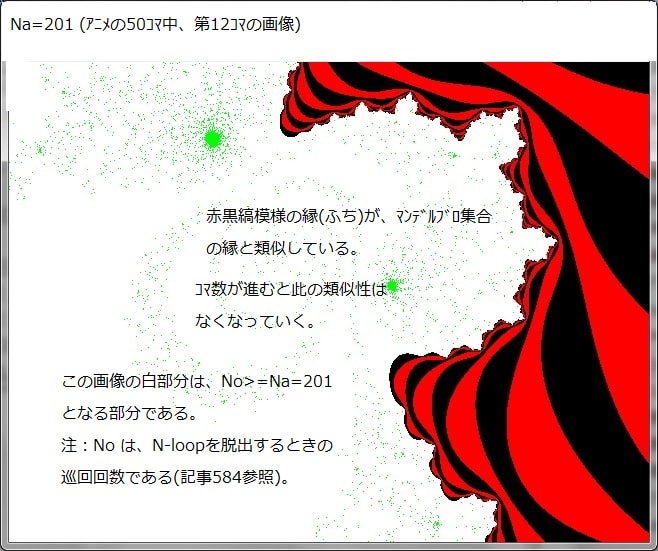
参考:下図はマンデルブロ集合画像(緑色)である。
----------------------------
この類似性は何を意味するのだろうか?
単なる偶然だろうか?
この類似( 厳密には異なるが「感じ」は似ている )は、Naの或る箇所のみで他のNaでは発生しない。
画像の白部分は、N-loopを脱出する回数:NoがNa以上となる部分である。
そのような部分がマンデルブロ集合の、恐らく一部分と相似になるNaが存在することが事実だとすれば不思議だ。
この類似性は此の画像領域だけなのか、あるいは他の画像領域にもあるのか全く不明である。
この類似性が事実だとすれば、マンデルブロ集合画像の神秘性が一つ増えることになる。
前記事583の赤黒縞模様画像が分岐していく様子をアニメ化したものが此れ→分岐の様子
------------------------------------------------------
この動画について解説する。
前記事で解説したように、
巡回式:Z←Z^2+C (Cは複素定数)を
点列:Z0,Z1,Z2,Z3,・・・,Zn,・・・,Znmax・・・・・・(1)
で表す。但し、Z0=C とする)。Zn の n は巡回回数に相当する。
***
複素平面座標範囲:Dでの全ての点Cには、その固有のNoが存在する。
Noとは、|Zn|>2 となる n である。
即ち、巡回ループ(N-loop)を脱出するまでの巡回回数である。
今、Naを与え、No<NaとなるC点のみ表示させるようにする。
そうすれば、巡回回数がNa以下の画像が得られる。
Naを小さな値から大きな値に順次変えて画像を表示させていけば、巡回回数Noが小さな順に・・・換言すればN-loopを早く脱出する順に・・・画像が表示されていく。
上のアニメはNaを小から大に時間変化させたときの画像の時間変化である。
動画の緑色の箇所は No>2000の部分である。nmax=5000。
具体的な画像表示方法を言葉で書くより、BASICプログラムで要点のみ書くほうが、わかり易いだろう。その方法を最後に書いておいた。
-----------------------------------------------------------
この動画より分かること。
・赤黒縞模様の本体は画面右上部から発生し・・・即ち其の部分がN-loopを早く脱出し・・・其の本体は、ほぼ同時に2本に分岐し相互に「ら線」状に「からまって」いく。この2本の分岐の「本流」は同一源のもので他の部位から派生したものではない。
・2本の分岐は互いに同一の早さで「ら線」状に「からまって」いく。即ち、N-loop脱出の早さは互いに同一である。
・本体部及び分岐部の「成長」の早さは連続的・・・但しリニアではない・・・であり、断続してない。
・本体部が「成長」していく途中で、赤黒縞模様部の内側部の境界線は、マンデルブロ集合の境界線によく似た形状が見られる。これは大変興味深い。しかし本体部の「成長」が進むにつれて、その形状はマンデルブロ集合の境界線とは似ても似つかぬ形状へと変化していく。
・赤黒縞模様の本体は2本に分岐し「ら線」状に「からまり」、一点へと収斂していく。その2本の分岐の赤黒の各節目から更に分岐が派生していくが、それらの分岐は2箇所(緑の箇所)へと収斂していく。
・いずれにしても、以上の赤黒縞模様部の「成長」・・・換言すれば、Noの変容・・・はスムーズで、秩序だっており非線形性は見られない。
----------------------------------------------------------------
・動画作成方法
先ず上図の全C点の座標位置情報(K,J)とNo情報(N)のデータを、シーケンシャル・ファイル化(ファイル名:DATA)しておく。動画のコマ数を50枚として、また各コマのパラメータをNとして、N=0→50変化させて50枚の画像を作る。
10 REM 動画の作成
20 OPEN "C:\DATA.DAT" FOR INPUT AS #1
51 EE=2.718281
52 N=0 ←N=0→50変化させて50枚の画像を作る。
60 NA=3.5*EE^(N/8)+185.5 ←これは試行して決めた。
70 INPUT #1,K,J,N
80 IF EOF(1) THEN 150
100 IF N 110 ZZ=N MOD 2
120 IF ZZ=0 THEN C=2 ELSE C=0
130 PSET (K,J),C
140 GOTO 70
150 CLOSE
160 END
この50枚の画像をNの順序に並べて0.2秒で再生させた。

上図はZ^2マンデルブロ画像の赤黒縞模様画像の一例である。
以下に赤黒縞模様画像の作成手順を詳しく説明する。
---------------------------------------------------------
巡回式:Z←Z^2+C (Cは複素定数)を
点列:Z0,Z1,Z2,Z3,・・・,Zn,・・・,Znmax・・・・・・(1)
で表す。但し、Z0=C とする。
|Zn|>2 ・・・・・・・・・・・・・・・・・(2)
いま、与えられた複素平面座標範囲:Dで点Cmを与え、点列(1)が初めて(2)を満足する点Znが存在すれば、点Cmを、n が偶数ならば黒、奇数ならば赤にして表示する。
同様なことを座標範囲:Dの全ての点Cで行えば、Dで赤黒縞模様画像が得られる。但し、点列(1)がZnmaxになっても(2)を満足しないときは当該点Cは何も表示しない。
(ちなみに、nmax→∞ でも(2)を満足しないような点Cの集合をマンデルブロ集合という。通常は適当な有限値に設定する)
マンデルブロ画像を作るとき、通常、C は D の長方形の上端の左端から右端へ、これを上端から下端へと繰り返して変化させる。此の方法でなくてもよい( 其の一例が極座標表示 )が此の手順が最も簡単である。
上図は此の手順で作成した画像である。点Cが与えられたとき、その点でのNoは点Cで異なってくる。
上図は、nmax=5000としていて、点Cが、No<700の場合のみ赤黒縞模様画像化している例である。画像から分かるように此の画像の場合は赤黒縞模様画像は特異な形をしている。
赤黒縞模様画像の赤黒が整然と連結しているということは、Noが規則正しく 1 ずつ変化していることを意味していて、その点でも此の画像が秩序をもっていることが分かる。
次に此の画像での座標範囲:Dを、以下で順に示していく。先ず元々のマンデルブロ画像から始まり、その中の部分を順次拡大していく。但し、画像の色は適宜変えているが、画像の形態には無関係だと思ってよい。ここでの関心事は、上の画像は、いかなる座標範囲:D なのか、だからだ。



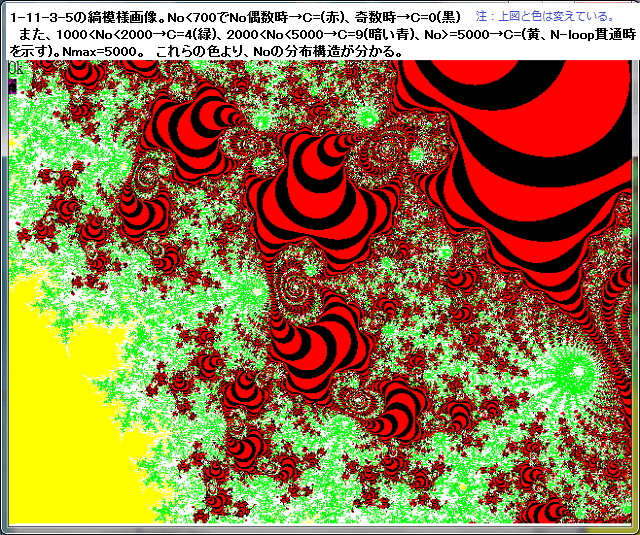

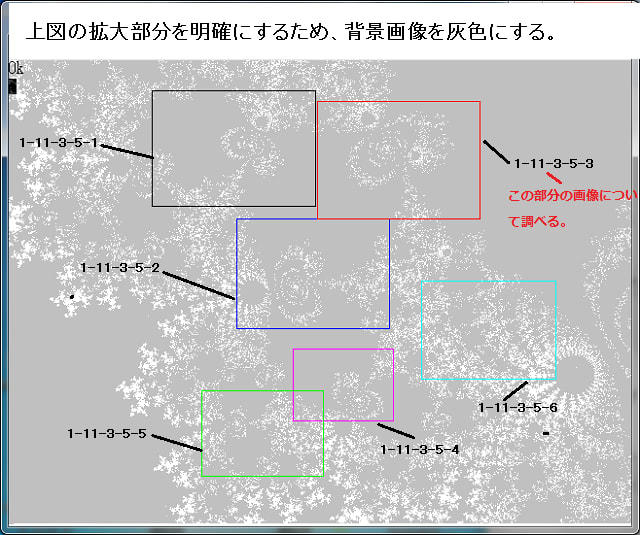
このように、座標範囲:D は 1-11-3-5-3 の部位である。
ちなみに、この1-11-3-5-3部位にある赤黒縞模様画像画像の中にある縞模様の「2本の絡まり」の拡大図を下図に示す。この画像の拡大率は最初の図に対して 1126871 倍にあたる。

また、下図は No<463 の場合の赤黒縞模様画像である。(緑の色の箇所は No>2000 の箇所である。)
この画像のほうが、赤黒縞模様画像 から分かる画像の特徴が理解しやすく、その特徴を下記しておく。

赤黒縞模様は分岐構造をしている。その分岐は更に複雑に分岐を重ね、大ざっぱに見て以下のような分布構造となっている。
***
1.分岐の本体部が存在し、その本体部の黒赤の節目、即ち、Noが1増すごとに新しい分岐が本体の両側から発生し、その発生した新しい分岐は、同様な分岐を繰り返していく。その場合の分岐部分の大きさと方向は随時変化していて一定ではない。
2.分岐の本体は、螺旋模様に或る一点へと収束していく。
3.2の場合、二本の別の本体が、螺旋模様となって共通の収束点へと向かうが、その螺旋は互いに、からまった状態(下図がその例)となっている。
4.本体部分から派生した複数の分岐は、他の派生した複数の分岐と集まっていき、同一座標点へと向かって収束している。
-------------------
関連記事:344,345
・複素関数:sinZ
・N-loop入力条件:|CXi|<2π,|CYi|<1.5π
・N-loop脱出条件:X^2+Y^2>2500
・Nmax=1000
・脱出時の色:C=No mod 16,C=6→5,C=7→8
・N-loop貫通時の色=黄色(sinZ マンデルブロ集合部分)
------------------------------

---------------------------------------------------------------


-------------------------------





放散虫:Z^2+0.5→Z^3+0.5 の変容 →Z^2+0.5→Z^3+0.5
放散虫:Z^1+0.5→Z^3+0.5 の変容 →Z^1+0.5→Z^3+0.5
放散虫:Z^2+sinZ+0.5 zoom1 →Z^2+sinZ+0.5
放散虫:Z^2+sinZ+0.5 zoom2 →Z^2+sinZ+0.5b
放散虫:Z^3+0.5の内臓部の「ら線階段」→Z^3+0.5a
Z^2マンデルブロ画像の分岐の成長1 →Z^2マンデルブロ画像1
Z^5+Cという名の万華鏡1 →Z^5+C1
Z^5+Cという名の万華鏡2 →Z^5+C2
Z^(e^Z)+μという名の万華鏡 →Z^(e^Z)+μ
Z^(e^Z)+μ画像の変容→Z^(e^Z)+μ(その2)

下図は、発散しない点C全てにおける、巡回計算過程での点Z(X,iY)の集合濃度画像である。ここで点Zが同一座標になる場合の回数(濃度)をmとし、BASIC/98での色コードをCCとすると、CC=LOG(m)で表現した。(参考:画像データは下に書いたプログラム1のDATA2に相当する。)
下図の下に、CCの色コードを示してあるから、点(X,iY)が同一座標となる濃度の形態が分かる。例えば、色が緑(CC=5)の場合、その点での濃度は、e^5=148となる。また下図においてマダラに見える黒部分はCC=0故、LOG(m)=0となり、m=1 となる。
但し、m=0 の場合は非表示(空白)とした(参考:下のフログラム3の行511)。
下図の左部分の空白は点(X,iY)が存在しない部分であるが、画像中の白スジ線の存在理由は不明である。

下図は上図に、マンデルブロ集合の境界線(白い線で示した)を重ね描きした画像である。
点(X,iY)の集合は、マンデルブロ集合より、一回り大きく、ぼやけてはいるが外形は似ているのが面白い。マンデルブロ集合の中央部と、左側の「こぶ」あたりに、点(X,iY)の濃度も大きくなっていることが色で分かる。

---------------------------------------------------------------
以下、画像作成のBASIC/98フログラムを示す。基本的に三つのプログラムから構成されている。
・プログラム1→発散しない点C全てにおける、巡回計算過程での点(X,Y)及び当該(K,J)をfile:DATA2に保存する。
10 REM マンデルブロー N-loopの内外保存
12 REM N-loopを脱出したデータ→DATA1
14 REM N-loopを脱出しない全データ→DATA2
16 REM N-LOOPを貫通したデータ→DATA3
20 REM 横軸(K):640 dots、縦軸(J):480 dots
30 CHAIN MERGE "C:\BASIC1\PRO\SUBR\ARCTAN3.BAS",40,ALL
40 CHAIN MERGE "C:\BASIC1\PRO\SUBR\TAN.BAS",50,ALL
50 '
60 CHAIN MERGE "C:\BASIC1\PRO\SUBR\KOSHIKI.BAS",70,ALL
70 CHAIN MERGE "C:\BASIC1\PRO\SUBR\ZFZ.BAS",80,ALL
80 CHAIN MERGE "C:\BASIC1\PRO\SUBR\FGZ.BAS",90,ALL
90 CHAIN MERGE "C:\BASIC1\PRO\SUBR\ER1.BAS",100,ALL
100 ON ERROR GOTO 50000
110 CONSOLE ,,0,1
120 COLOR 0,7,,,2
130 CLS 3
140 GOSUB 10000
150 OPEN "C:\BASIC1\RUN\DATA1.DAT" FOR OUTPUT AS #1
152 OPEN "C:\BASIC1\RUN\DATA2.DAT" FOR OUTPUT AS #2
154 OPEN "C:\BASIC1\RUN\DATA3.DAT" FOR OUTPUT AS #3
160 OPEN "C:\BASIC1\RUN\親DATA.DAT" FOR OUTPUT AS #4
170 REM 親DATAの設定(随時変更)
180 CXS=-2.5 :CXE=0.5
190 DX=(CXE-CXS)/640 :DY=DX:CYS=-240*DY
200 WRITE #4,CXS,CXE,CYS,CYE,DX,DY
210 CLOSE #4
220 FOR J=0 TO 480
230 LOCATE 0,0:PRINT J
240 FOR K=0 TO 640
260 CX=CXS+DX*K
270 CY=CYS+DY*J
272 X=0:Y=0
280 FOR N=0 TO 500
290 XX=FNR2(X,Y)+CX
300 Y=FNI2(X,Y)+CY
310 X=XX
320 Q=X^2+Y^2
330 IF Q>4 THEN 380
336 WRITE #2,X,Y,K,J,N
340 NEXT N
342 WRITE #3,X,Y,K,J,N
360 GOTO 420
380 WRITE #1,X,Y,K,J,N
420 NEXT K
430 NEXT J
440 END
・フログラム2→ DATA2の(X,Y)の表示座標系(K,J)への変換し(行170)、同一座標値の濃度を求める(行150~240)。その場合、行200より濃度は+1余計加算されている。また表示座標系(K,J)
での各点(X,Y)の最大濃度を求め(行250-300)、file:DAT2Aに保存する(行280)。
10 REM DATA2のX,YのKK,JJ化と、点(KK,JJ)の濃度をZ(KK,JJ)に
12 REM 保存していき、(KK,JJ,Z(KK,JJ))のデータ:DATA2Aを求める。
14 CHAIN MERGE "C:\BASIC1\PRO\SUBR\ER2.BAS",16,ALL
16 ON ERROR GOTO 50000
20 OPEN "C:\BASIC1\TEST\DATA2A.DAT" FOR OUTPUT AS #2
30 OPEN "C:\BASIC1\TEST\DATA2.DAT" FOR INPUT AS #1
40 CONSOLE ,,0,1
50 COLOR 0,7,,,2
60 CLS 3
70 CXS=-2.5:CXE=0.5:DX=(CXE-CXS)/640:DY=DX
80 CYS=-240*DY:CYE=-CYS:M=0
90 DIM Z(640,480)
100 FOR I=0 TO 480
110 FOR II=0 TO 640
120 Z(KK,JJ)=0
130 NEXT II
140 NEXT I
150 INPUT #1,X,Y,K,J,N
160 IF EOF(1) THEN 242
170 KKK=(X-CXS)/DX: JJJ=(Y-CYS)/DY
180 KK=INT(KKK):JJ=INT(JJJ)
190 IF KK>640 OR JJ>480 THEN 240
191 IF KK<0 OR JJ<0 THEN 240
200 Z(KK,JJ)=Z(KK,JJ)+1
202 C=Z(KK,JJ) MOD 16:PSET(KK,JJ),C
212 M=M+1:LOCATE 0,0:PRINT M
240 GOTO 150
242 CLS 3
250 REM KK,JJ,Z(KK,JJ)の保存→DATA*A
260 FOR JJJ=0 TO 480
270 FOR KKK=0 TO 640
271 IF Z(KKK,JJJ)=0 THEN 290
280 WRITE #2,KKK,JJJ,Z(KKK,JJJ)
282 CC=Z(KKK,JJJ) MOD 16:PSET (KKK,JJJ),CC
290 NEXT KKK
300 NEXT JJJ
410 END
・フログラム3 →DATA2A(濃度データ)の表示。
10 REM 画像表示
30 CONSOLE ,,0,1
40 COLOR 0,7,,,2
50 CLS 3
51 CHAIN MERGE "C:\BASIC1\PRO\SUBR\COLOR左下表示.BAS",55,ALL
55 OPEN "C:\BASIC1\RUN\DATA2A.DAT" FOR INPUT AS #1
60 INPUT #1,K,J,Z
62 LOCATE 0,0:PRINT USING "###";J
64 LOCATE 0,1:PRINT USING "###";K
70 IF EOF(1) THEN 120
80 REM Zによる色の区別:サブルーチン
90 GOSUB 500
100 PSET (K,J),C
110 GOTO 60
120 CLOSE #1
130 GOTO 600
500 REM Zによる色の区別:最初からZは1加算されているから補正をする
510 Z=Z-1
511 IF Z=0 THEN 550
520 C=LOG(Z)
550 RETURN
600 GOSUB 3000
610 END
・フログラム4 →画像表示及びマンデルブロ集合の境界線の表示
10 REM 画像表示及びマンデルブロ集合の境界線の表示
30 CONSOLE ,,0,1
40 COLOR 0,7,,,2
50 CLS 3
51 CHAIN MERGE "C:\BASIC1\PRO\SUBR\COLOR左下表示.BAS",52,ALL
55 OPEN "C:\BASIC1\RUN\DATA2A.DAT" FOR INPUT AS #1
60 INPUT #1,K,J,Z
62 LOCATE 0,0:PRINT USING "###";J
64 LOCATE 0,1:PRINT USING "###";K
70 IF EOF(1) THEN 120
80 REM Zによる色の区別:サブルーチン
90 GOSUB 500
100 PSET (K,J),C
110 GOTO 60
120 CLOSE #1
130 GOTO 600
500 REM Zによる色の区別:最初からZは1加算されているから補正をする
510 Z=Z-1
511 IF Z=0 THEN 550
520 C=LOG(Z)
550 RETURN
600 GOSUB 3000
610 REM 旧data1からマンデルブロ画像の境界付近の画像の読み込み
620 OPEN "C:\BASIC1\RUN\DATAmandel.DAT" FOR INPUT AS #1
630 INPUT #1,K,J,N
640 IF EOF(1) THEN 670
650 PSET (K,J),0
660 GOTO 630
670 CLOSE
680 END
位相平面の各座標の軌跡通過数を m としたとき、
(a)色:C=m mod 16
(b)色:C=log(m) mod 16
を比較する。
(a)の場合の m 色コード:Cの順序どおりになる。
但し、m=0の場合はプログラムで白としており、C=7(白)の場合は C=8(灰)としている。
mod を使用しているから、m は16進で変化する。
(b)の場合はm=e^C だから、
C=0(黒)ならば m=e^0.5=1
C=1(青)ならば m=e^0.5~1.5=1~4
C=2(赤)ならば m=e^1.5~2.5=4~12
C=3(橙)ならば m=e^2.5~3.5=12~33
C=4(緑)ならば m=e^3.5~4.5=33~90
C=5(青)ならば m=e^4.5~5.5=90~247
C=6(黄)ならば m=e^5.5~6.5=247~665
C=8(灰)ならば m=e^6.5~8.5=665~4915
となる。但し、m=0 の場合は白としている。
以下に示す(b)の画像の色から分かるように、m は 16 以上となっており、C=0~15が16進で表示されるため結果として画像の色が混濁してしまい、画像の色構造が不鮮明となってしまっている。
(b)の画像では、log 効果により色が整理され、その結果、画像の色構造(即ち、軌跡の通過濃度分布構造)が判然としてくる。
以下に(a)(b)を対比した画像を示す。
--------------------------------------



---------------------------------------


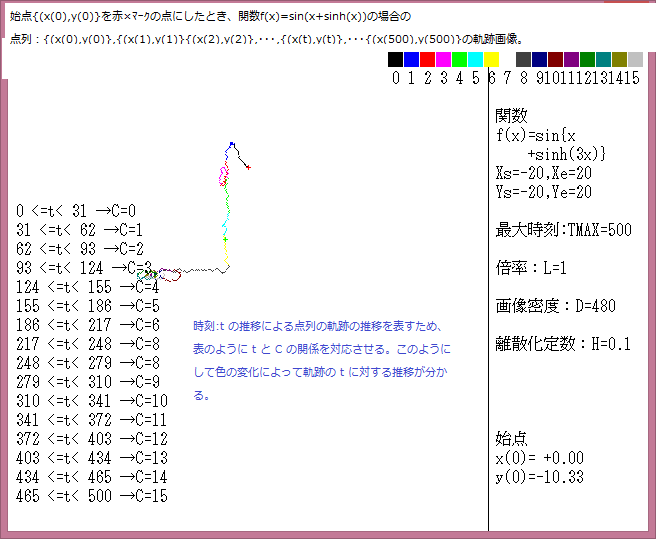
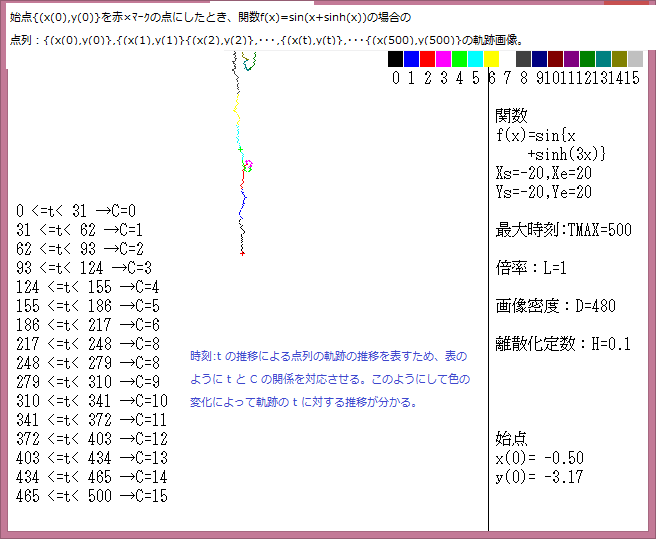
今回は始点が、px表示で、以下の3つの近接点の軌跡の挙動を調べる。
①(120,120),(121,121)
②(242,240),(243,240)
③(242,240),(244,240)
詳細なパラメーター値は各画像に書いてある。
----------------------------------------------------


------------------------------------


------------------------------------




-------------------------------------------

T(3)=4x^3-3xとなる。(『コンピューター、カオス、フラクタル』(C.Aピックオーバー著、白揚社)、p.379)
そこで、関数:f(x)=sin(T(3)) の軌跡濃度画像を求めてみる。各パラメータは下図に書いてある。
D=480,Tmax=500,L=3,H=0.05の画像構造は、記事571のf(x)=sin{x+sinh(x)}のD=150,Tmax=500,L=3,H=0.5の画像構造と似ている。
其れは、f(x)=sin(T(3)) とf(x)=sin{x+sinh(x)} が近似しているためだろう。
---------------------------------------------


------------------------------------------

-----------------------------------------
参考: f(x)=sin(x+sinh(x)), D=150,Tmax=500, L=3 画像

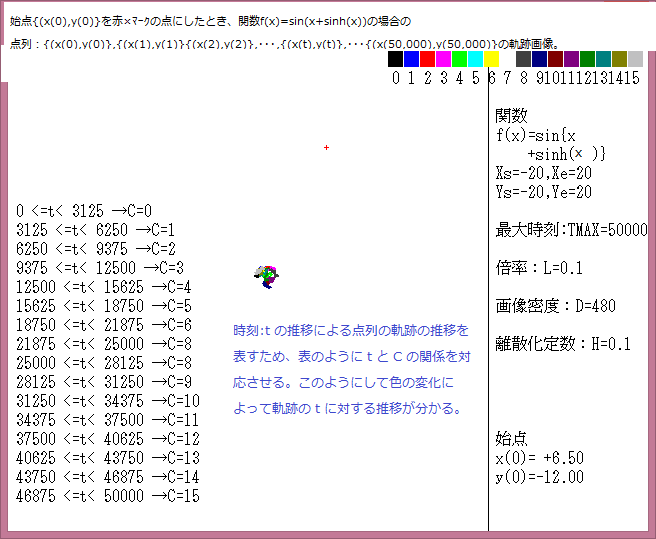
マウスで与えた始点は赤色の×で示し、軌跡の時間変化は色で表示している。具体的パラメータの値は下図に示した。
Tmax=500同様にTmax=50,000の場合も軌跡の形は始点の座標によって全く異なっている。また軌跡の形はブラウン運動のようにランダムに移動する場合もあり、軌跡の形態は極めて複雑である。
要するに Tmax=50,000でも軌跡の形態は本質的変化は見られない。
---------------------------------------------------------


-----------------------------------


------------------------------------


-----------------------------------


----------------------------------


表示範囲は|x(t)|

f(x)=sin(x+sin(3x))
f(x)=sin(x^2+sin(3x))
f(x)=sin(x+tan(3x))
f(x)=sin(x+sin(x)sin(3x))
f(x)=sin(x+sinh(x))
今回の記事は以下の関数の濃度分布画像を求める。但し、表示範囲は|x(t)|<=20,|y(t)|<=20及びパラメーターは、D=50,Tmax=50,H=0.1,L=1とする。
f(x)=sin(x+log|x|)
f(x)=sin(x+e^x)
f(x)=sin(log|x|)
f(x)=sin(x+sin(3x+sin(2x)))
これらの4つの関数の画像を以下の色表示で示す。
(a)色:C=log(m) mod 16,但しC=7→8,m=0→非表示
(b)色:C=m mod 16,但しC=7→8,m=0→非表示
ここで、m は座標点を通過する軌跡の数である。
また、色表示(a)の場合のmは以下のとおりとなる。
m=e^C だから、
C=0(黒)ならば m=e^0.5=1
C=1(青)ならば m=e^0.5~1.5=1~4
C=2(赤)ならば m=e^1.5~2.5=4~12
C=3(橙)ならば m=e^2.5~3.5=12~33
C=4(緑)ならば m=e^3.5~4.5=33~90
C=5(青)ならば m=e^4.5~5.5=90~247
C=6(黄)ならば m=e^5.5~6.5=247~665
C=8(灰)ならば m=e^6.5~8.5=665~4915
となる。但し、m=0 の場合は白としている。
----------------------------------


-----------------------------------


-----------------------------------


----------------------------------


画像の構造は今迄の使用した関数とは全く違ってしまう。
このような力学サイクル系離散時間位相平面について解説は記事541を参照。ここで記事541の(3)式で、sin(ρx)を sinh(x) に変えた。その理由は特になく、このようにしたら画像はどうなるか?という興味だけである。
今回の画像は、始点が画像表示画面の全てのピクセル(480×480)の画像である。
位相平面の各座標の軌跡通過数を m としたとき、
色:C=log(m) mod 16
で表示している。log表示により位相平面の軌跡濃度が単純化され、濃度構造が分かり易くなる。
m=e^C だから、
C=0(黒)ならば m=e^0.5=1
C=1(青)ならば m=e^0.5~1.5=1~4
C=2(赤)ならば m=e^1.5~2.5=4~12
C=3(橙)ならば m=e^2.5~3.5=12~33
C=4(緑)ならば m=e^3.5~4.5=33~90
C=5(青)ならば m=e^4.5~5.5=90~247
C=6(黄)ならば m=e^5.5~6.5=247~665
C=8(灰)ならば m=e^6.5~8.5=665~4915
となる。但し、m=0 の場合は白としている。
下図から分かるように軌跡濃度は極めて美しい秩序構造を形成している。

マウスで与えた始点は赤色の×で示し、軌跡の時間変化は色で表示している。具体的パラメータの値は下図に示した。
下図から分かるように、軌跡の形は始点の座標によって全く異なっている。また軌跡の形はブラウン運動のようにランダムに移動する場合もあり、軌跡の形態は極めて複雑である。
前記事561の最初の図形(D=50,TMAX=50,L=1,H=0.1の画像)の中央以外の部分の軌跡濃度のランダム性は各始点での軌跡のランダム性に異存しているのであろう。また此の濃度画像の中心部近辺の濃度画像は明確な或る種の規則性と秩序があり・・・その濃度構造が面白いのだが・・・その規則性と秩序は、その部分の始点の軌跡に規則性と秩序が存在していることを暗示している。
------------------------------------------------------------


-----------------------------

----------------------------


----------------------------


----------------------------

------------------------------


------------------------------


---------------------------------


-------------------------------


------------------------------











