608 Z^f(Z)+Ｃ 画像 (その３)

下図は以下の画像である。

・複素関数は、Z^f(Z) で、f(Z) は、前記事同様、sin Z , cosh Z, e^Z, Z^2, Z^3, Z^4 の 6 種類。

・N-loop脱出条件は、『Q=1/(log|X|log|Y|)として、もし、(|Q|＞10 or |Q|＜0.1 ならば脱出する』。　

・pset条件は、『N-loop脱出後、もし、(|X|＜10 or |Y|＜10)ならば、psetする』。

下図は、上記条件の 6 種類の関数の画像の一括表示したもので、下図の上段左より、f(Z)= sin Z , cosh Z, e^Z　。下段左より、f(Z)=Z^2, Z^3, Z^4。



次に、6 種類の関数の画像を個別に紹介します。
sin Z , cosh Z, e^Z, Z^2, Z^3, Z^4 の順に示す。

607 Z^f(Z)+C 画像 (その２)

下図は以下の画像である。

・複素関数は、Z^f(Z)+C で、f(Z) は前回同様　sin Z , cosh Z, e^Z, Z^2, Z^3, Z^4 の 6 種類。

・N-loop脱出条件は『Q=tan(XY)として、もし、(|Q|＞100 or |Q|＜0.01 ならば脱出する』。　

・pset条件は『N-loop脱出後、もし、(|X|＜10 or |Y|＜10)ならば、psetする』。

下図は、上記条件の 6 種類の関数の画像の一括表示したものである。
下図の上段左より、f(Z)= sin Z , cosh Z, e^Z　。下段左より、f(Z)=Z^2, Z^3, Z^4。



次に、6 種類の関数の画像を個別に、sin Z , cosh Z, e^Z, Z^2, Z^3, Z^4 の順に示す。

606 Z^f(Z)+C 画像 (その1)

下図は以下の画像である。

1.複素関数：Z^f(Z)+o.5 にて、上図上段左より、f(Z)=sinZ , coshZ , e^Z　下段左より、f(Z)=Z^2 , Z^3 , Z^4
2.N-loop脱出条件：もし、X^2+Y^2＞100　ならば脱出する。
3.pset条件：もし、(|X|＜10 or |Y|＜10) ならばpsetする。



下図は、上図の上段右画像の縮小・拡大図である。
即ち、N-loop入力：|Xi|＜1.5L , |Yi|＜0.75L にて、
上図上段左より、L=0.5 , 0.8 ,1　下段左より、L=2, 3, 4



***

下図は以下の画像である。
1.複素関数：Z^(e^Z)+o.5
2.N-loop脱出条件：もし、X^2+Y^2＞100　ならば脱出する。
3.pset条件：もし、(|X|＜10 or |Y|＜10) ならばpsetする。

605 Z^Z+C の変容 (その2)

今回の画像は以下の作成条件の画像である。

・複素関数：Z^Z+C (C は 12 種類)
・N-loop脱出条件：『Q=X^2+Y^2 として、もし、Q＞100 ならば脱出する』　
・pset条件：『N-loop脱出後、もし、(|X|＜10 or |Y|＜10)ならば、psetする』

以下の図は、Z^Z+C において、s=0.1→0.3→0.5→0.7→0.9→4.5 と変えたときの画像の変容である。(但し、N-loop入力範囲は、|Xi|＜1.5,|Yi|＜1.7 )



以下の図は、Z^Z+C において、s=0.8→0.85→0.9→0.95→1→1.05 と変えたときの画像の変容である。(但し、N-loop入力範囲は、|Xi|＜4.5,|Yi|＜5.0 )



以下の図は、Z^Z+C において、C=0.7 と C=0.9 の場合の画像である。(但し、N-loop入力範囲は、|Xi|＜4.5,|Yi|＜3.3 )

604 Z^Z+Z^s+0.5 の変容

今回は以下の条件の画像である。

・複素関数：Z^Z+Z^s +0.5 (s は 12 種類)
・N-loop脱出条件：『Q=(X-Y)^3 として、もし、(|Q|＞100 or |Q|＜0.1 ならば脱出する』　(注：この条件が前回の記事603と異なっています。
・pset条件：『N-loop脱出後、もし、(|X|＜10 or |Y|＜10)ならば、psetする』

以下の図は、Z^Z+Z^s+0.5 において、s=2→2.5→3→3.5→4→4.5 及び、s=5→5.5→6→6.5→7→7.5　と変えたときの変容画像である。





下図は、s=3 の場合の拡大画像である。

603 Z^Z+Z^s+C の変容画像

今回の画像は、複素関数：Z^Z+Z^s+C ,(C=0.3) において、s=1→24 変化させたときの画像の変容である。

先ず、s=1→6 の場合の変容が下図である。



次に、s=7→24 の場合の変容が下図である。下図は上図の 2 倍に拡大している。s が 7 以上では 変容は、ほとんど変化していないことが分かる。







次に、複素関数の C を、0.3→2 に変えて、上と同様に、s=1→24 まで変えてみる。先ず、s=1→6 の場合の変容が下図である。



次に、s=7→12 の場合の変容が下図である。下図は上図の 2 倍に拡大している。



上図では“内臓”部が表示されていない。表示できるように、N-loop脱出条件『もし、Q=X^2+Y^2＞Tならば脱する』のTを、T=10→5 に変更した。

その変更条件での、s=7→24 の場合の変容が下図である。
下図において、青い変な“虫”が入った目玉模様の図が、ちょうど、s 個、円状に並んでいることが分かる。







以上の画像より、複素関数：Z^Z+Z^s+C の、s の変化による変容は、C が小さいとき(例：C=0.3)は、Z^s 項は、あまり寄与せず、C 大きいとき(例：C=2)は寄与している、ということが分かる。

602 放散虫：Z^Z+Z^6+0.5 の変容

今回紹介するのは、以下の条件の画像である。

・複素関数：Z^Z+Z^6 +C (Cは実数の定数)
・N-loop脱出条件：『X^2+Y^2＞10 ならば脱出する』
・即ちpset条件：『N-loop脱出後、もし、(|X|＜10 or |Y|＜10)ならば、psetする』

以下の図は、“放散虫：Z^Z+Z^6+0.5” の外形図で、C を6種類、変えたときの、その変容像である。



以下の図は、“放散虫：Z^Z+Z^6+0.5” の“内臓”部で、C を6種類、変えたときの、その変容像である。



以下の図は、C=0.1 と、C=0.3と、C= 2.0の場合の拡大図である。







------------------------------

関連記事：070

601 Z^Z +C 画像 の変容

以下の図は、Z^Z+C の、C を6種類、変えた画像の連続画像と其の個別の画像である。画像作成条件は最後に書いておく。


--------------------------------------------------














画像作成条件

・複素関数：Z^Z +C (Cは実数の定数)
・N-loop脱出条件：『Q=TAN(X*Y)』としたとき、もし、(|Q|>10 0or |Q|<0.01)ならば脱出する』
・即ちpset条件：『N-loop脱出後、もし、(|X|<10 or |Y|<10)ならば、psetする』

600 e^(Z^2) +C の変容画像

上図の画像作成条件は以下のとおり。

・複素関数：e^(Z^2) +C (C=0.1, 1, 1.5, 2)
・N-loop脱出条件：『Q=1/(log|X|*log|Y|』としたとき、もし、(|Q|>10 or |Q|<0.1)ならば脱出する』
・pset条件：『N-loop脱出後、もし、(|X|<10 or |Y|<10)ならば、psetする』

599 e^Z+C 画像のアニメ

前記事596で示した画像:e^Z+C (Cは実定数)にて、C=0.01→2 までリニアに変化させたらどんな動画になるか試してみた。以下、その動画。

e^Z+C,C=0.01→2 の動画　→　その動画


-------------------------------------------
ちなみに此の動画画像作成条件を再掲しておく。

・複素関数：e^Z +C (C=0.01→2)
・N-loop脱出条件：『Q=1/(logX*logY』としたとき、もし、
(|Q|>10 or |Q|<0.1)ならば脱出する』
・pset条件：『N-loop脱出後、もし、(|X|<10 or |Y|<10)ならば、psetする』
・画像表示範囲：0<=Yi<=2π, |Xi|<=2π/640*240=0.75π

598 e^Z +C 画像 (その2)

今回の画像は前記事597の画像を縦軸方向を移動させた画像。
画像作成条件の他の条件は前記事597と同じ。

597 e^Z +C 画像

今回の画像の作成条件は以下のとおり。

・複素関数：e^Z +C (Cは実数の定数)
・N-loop脱出条件：『Q=1/(logX*logY』としたとき、もし、
(|Q|＞10 or |Q|＜0.1)ならば脱出する』
・pset条件：『N-loop脱出後、もし、(|X|＜10 or |Y|＜10)ならば、psetする』
・画像表示範囲：0＜=Yi＜=2π, |Xi|＜=2π/640*240=0.75π
以下は、この条件での画像。

596 アニメ：連続したジュリィア集合画像(その4)

上図の赤点に対応するジュリィア画像が下図である。



下図は、上図においてNo (N-loop脱出時のN値) が偶数の時→赤、奇数の時→黒 にした画像である。



上の画像において、No (即ち、N-loopを脱出する時のN値) を、小さい順に表示させていった動画を示す。

Noを小さい順に表現した動画→　その動画

『Noが小さい順』とは換言すれば、『N-loopを早く脱出する』と同意である。

今迄のマンデルブロ画像やジュリィア画像でも、そうであったが、この画像においても、『ら線』画像が随所にあり、今迄に示した画像においては、その『ら線』反時計方向に収斂していった。

今回の画像は、動画及び下図の静止画像でも分かるように、『ら線』が反時計方向へ収斂していく部分と、時計方向に収斂していく部分とに分岐している画像構造になっている。



------------------------------------------------
このジュリィア画像の『ら線』の部分の拡大図は記事359で掲載している。
以下は此の記事での画像である。

下図が反時計方向に収斂する『ら線』の拡大図である。




下図が時計方向に収斂する『ら線』の拡大図である。

595 Z^2マンデルブロ点列における、Z0～Z15の軌跡の変容

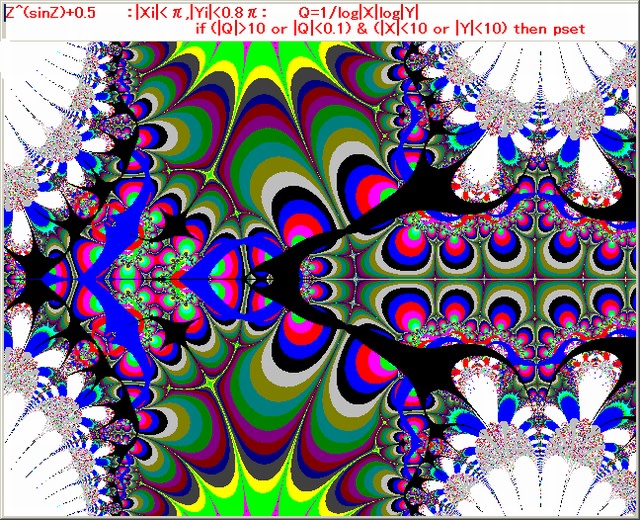
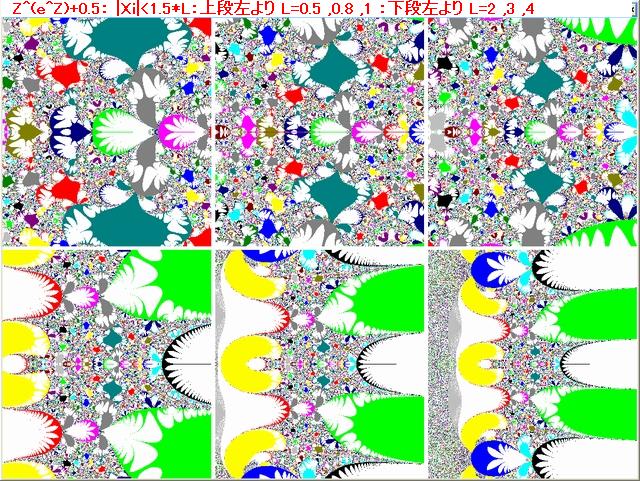
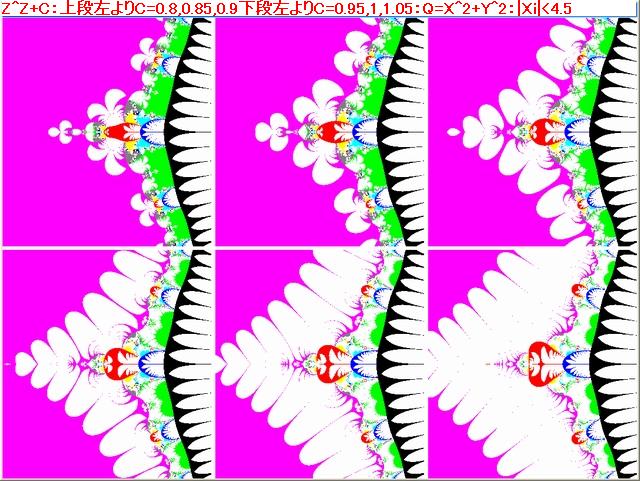
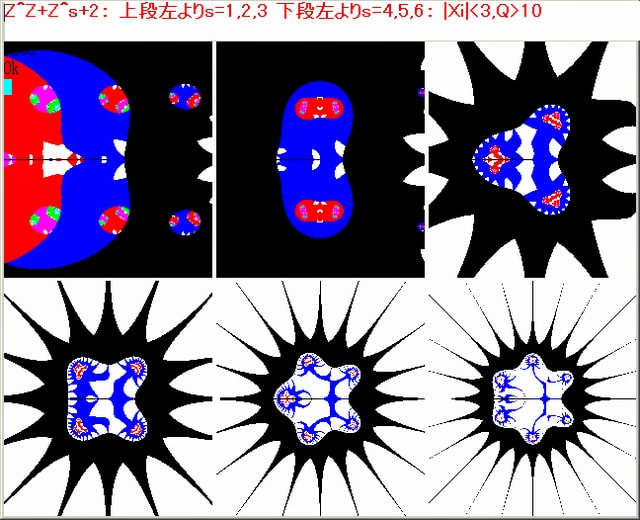
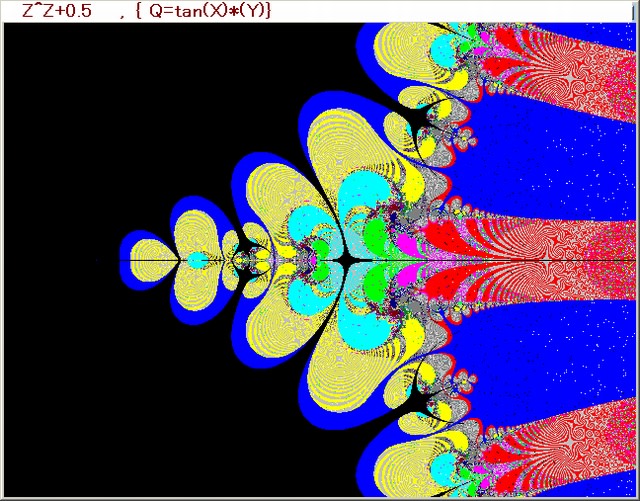
前記事595では、Z^2マンデルブロ点列における、Z0及びZ15～Z15の軌跡の変容の動画を掲載した。

今回は、Z0～Z15の点列、即ち、

Z0,Z1,Z2,・・・,Zn,・・・Z15 ・・・・・・・・・・・・・・・・・・・・・・・(1)

の軌跡の変容を表す動画を紹介する。　

Z0～Z15の点列の動画→　Z0～Z15の点列の挙動

***

この動画の詳細な解説は記事588を参照。ここで概略な説明をしておく。

巡回式:Z←Z^2+λは、点列(1)で表される。ここで、λは複素定数。

ここで、Z0=λ とする。

極座標を用いて、半径λの円における点列(1)の挙動画像を求める。

この場合、点Znの色はBASIC/95のカラーコード番号nに一致させている(カラーコードは画像の右上に示してある)。

Z0=λは、半径=λの黒(n=0)で表示される。そして例えば Z1 は青色(n=1)で表示される。

ここで、λを 0.11→1.36 step 1 ずつ増加させていく。

***

この動画で興味深いのは以下のことだ。(記事595と基本的に同じ。)

-----------------------------

1.点Z0(黒い円)がマンデルブロ集合内の或る範囲内では、Z1～Z15も近似的な円を描く。その場合、その円の大きさはZnのnに従って振動している。

2.更に、点Z0(黒い円)がマンデルブロ集合内の或る範囲内で増加していくと、Z1～Z15は捻じれた「ら線」状曲線を描き始め、Z0の増加につれて其の「ら線」も増大していく。

2.点Z0(黒い円)がマンデルブロ集合の境界に達すると、Z1～Z15の曲線は混沌とした錯乱状態の「乱舞」を呈するようになる。

3.その錯乱した「乱舞」は、点Z0(黒い円)がマンデルブロ集合の「頭部」の境界を過ぎるまで続く。

4.点Z0(黒い円)がマンデルブロ集合の「頭部」の境界を過ぎると、Z1～Z15の曲線は「柔らかな舞い」になる。

----------------------------

Z1～Z15の挙動は明らかにマンデルブロ集合の境界線と密接な関係があり、その挙動の複雑さには或る法則が存在するに違いたないだろうが、「錯綜とした乱舞」のような文学的表現でしか私は表せない。

ともあれ、マンデルブロ画像及び其の点列の不思議さと美しさを感じざるを得ない動画だ。。

***

ここで上の動画の具体的数値を示しておく。

K=0→50000 従って、dθ=2π/50000=0.000126rad
J=0→240, Rmax=1.36 従って、dR=1.36/240=0.00567
表示画像の中心点=マンデルブロ画像の重心座標値=(-0.14,0)
点列の極座標値はマンデルブロの重心座標値に一致させるように、(-0.14,0)だけ平行移動させている。
従って点列座標値はマンデルブロ集合画像座標値と一致する。
-------------------------------------------------------
参考のためにBASIC/98のプログラムを下記しておく。
注：KMAXはRの大きさによって適宜変えた。

10 REM マンデルブロ点列：Z0～Z15
12 CHAIN MERGE "C:\BASIC\PRO\SUBR\COLOR右上表示.BAS",50,ALL
50 CHAIN MERGE "C:\BASIC\PRO\SUBR\KOSHIKI.BAS",80,ALL
80 CHAIN MERGE "C:\BASIC\PRO\SUBR\ER1.BAS",90,ALL
90 ON ERROR GOTO 50000
91 CONSOLE ,,0,1
92 COLOR 0,7,,,2
93 CLS 3
94 GOSUB 10000
100 GOSUB 3000
101 PSET(320,240),2
102 OPEN "C:\BASIC1\RUN\DATAマンデルC.DAT" FOR INPUT AS #2
103 IF EOF(2) THEN 107
104 INPUT #2,X,Y
105 PSET (X,Y),0
106 GOTO 103
107 CLOSE #2
110 OPEN"C:\BASIC1\RUN\DATA.DAT" FOR OUTPUT AS #1
120 JMAX=240:KMAX=50000:RMAX=1.36:X0=-0.14:Y0=0
130 DR=RMAX/JMAX:DTH=2*P/KMAX:AA=JMAX/RMAX:NMAX=15
132 CXS=-1.5:D=1.36/320:CYS=-240*D:DTHDO=180*DTH/P
142 N1=220
150 J=20+N1
160 R=J*DR
170 LOCATE 0,0:PRINT "Z0,～Z15の軌跡の変容"
176 LOCATE 0,2:PRINT "Znの色はcolor code No.n"
183 LOCATE 0,3:PRINT "とすると色=n,但しn=7→8とする"
184 '
190 FOR K=0 TO KMAX
200 TH=K*DTH:THH=TH
206 CX=R*COS(TH)+X0
220 CY=R*SIN(TH)+Y0
221 X=0:Y=0
230 FOR N=0 TO NMAX
240 X1=X
250 X=FNR2(X,Y)+CX
260 Y=FNI2(X1,Y)+CY
270 Q=X^2+Y^2
272 K1=(X-CXS)/D:J1=(Y-CYS)/D
273 IF K1<0 OR J1<0 THEN 310
274 IF K1>640 OR J1>480 THEN 310
282 C=N
292 IF C=7 THEN C=8
300 PSET (K1,J1),C
310 NEXT N
390 NEXT K
400 CLOSE #1
520 END

594 アニメ：連続したジュリィア集合画像(その3)

前回の記事593では、Zc=-0.62-0.68i でのジュリィア集合画像及び其の全体画像を示した。

下図がそれらである。






今回は此の画像において、No (即ち、N-loopを脱出する時のN値) を、小さい順に表示させていった動画を示す。

Noを小さい順に表現した動画→　その動画

『Noが小さい順』とは換言すれば、『N-loopを早く脱出する』と同意である。

今迄のマンデルブロ画像でも、そうであったが、この画像においても、『ら線』画像が随所にあり、それらは、またしても、反時計方向に収斂していく。その様子が上の動画でも、よく分かる。

記事591のマンデルブロ画像の分岐もそうであったように、何故、この動画の『ら線』も反時計方向に収斂していくのだろう？

マンデルブロ画像もジュリィア画像も本質的には同じだから、その理由も同じだろうが、私には不思議である。