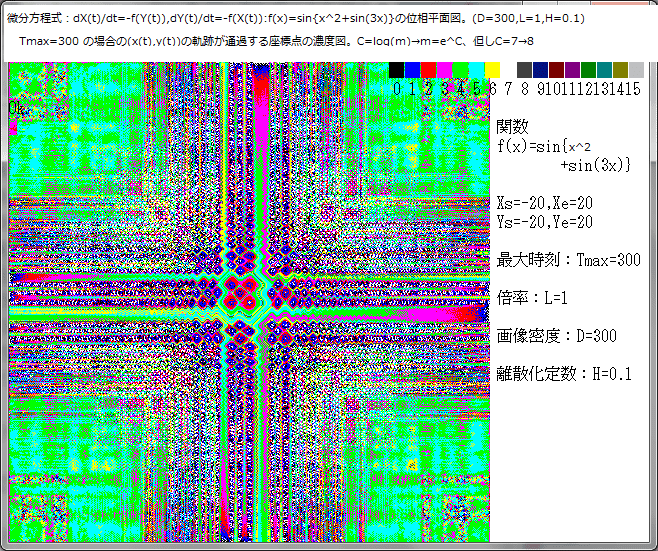
画像の関数は、f(x)=sin{x^2+tan(3x)}の場合、D=300, Tmax=300, H=0.05 としてLを変化(L=1,2,3,4,5)させた場合の画像を示す。
***
位相平面の各座標の軌跡通過数を m としたとき、
色:C=log(m) mod 16 の場合と
色:C=m mod 16 の場合を比較する。
画像のlog化については記事543を参照。
C=log(m) mod 16 の場合については、
m=e^C だから、、
C=0(黒)ならば m=e^0.5=1
C=1(青)ならば m=e^0.5~1.5=1~4
C=2(赤)ならば m=e^1.5~2.5=4~12
C=3(橙)ならば m=e^2.5~3.5=12~33
C=4(緑)ならば m=e^3.5~4.5=33~90
C=5(青)ならば m=e^4.5~5.5=90~247
C=6(黄)ならば m=e^5.5~6.5=247~665
C=8(灰)ならば m=e^6.5~8.5=665~4915
となる。但し、m=0 の場合は白としている。
C=m mod 16 の場合については、下図の場合は C=m としてよい。
***
Lは表示画像平面の中心点を固定したときの倍率である。
Lを大にするほど、点(x(t),y(t))の軌跡は大となり、従って表示画像範囲内外を、より広く飛び回り且つTmaxは有限のため其の結果として表示座標での m は相対的に小さくなり、画像濃度は減少する。従って、L を大にする即ち画像を拡大した場合、画像の構造は保持されるが濃度の色自体は変化する。
---------------------


---------------------
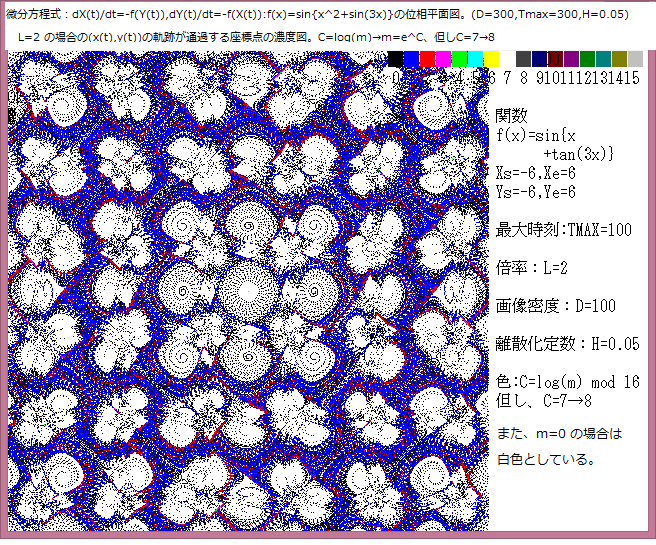

--------------------


--------------------


--------------------


***
位相平面の各座標の軌跡通過数を m としたとき、
色:C=log(m) mod 16 の場合と
色:C=m mod 16 の場合を比較する。
画像のlog化については記事543を参照。
C=log(m) mod 16 の場合については、
m=e^C だから、、
C=0(黒)ならば m=e^0.5=1
C=1(青)ならば m=e^0.5~1.5=1~4
C=2(赤)ならば m=e^1.5~2.5=4~12
C=3(橙)ならば m=e^2.5~3.5=12~33
C=4(緑)ならば m=e^3.5~4.5=33~90
C=5(青)ならば m=e^4.5~5.5=90~247
C=6(黄)ならば m=e^5.5~6.5=247~665
C=8(灰)ならば m=e^6.5~8.5=665~4915
となる。但し、m=0 の場合は白としている。
C=m mod 16 の場合については、下図の場合は C=m としてよい。
***
Lは表示画像平面の中心点を固定したときの倍率である。
Lを大にするほど、点(x(t),y(t))の軌跡は大となり、従って表示画像範囲内外を、より広く飛び回り且つTmaxは有限のため其の結果として表示座標での m は相対的に小さくなり、画像濃度は減少する。従って、L を大にする即ち画像を拡大した場合、画像の構造は保持されるが濃度の色自体は変化する。
---------------------


---------------------


--------------------


--------------------


--------------------