226 ヴェルンハルスト方程式画像(その3)

ヴェルンハルスト方程式は下記で示される漸化式であった。(記事274参照)
　　X(t+1)=A{X(t)(1-X(t)}

即ち、初期値を t=0 の時のX(0)とすれば、上式より次の数列が得られる。

X(0),X(1),X(2),X(3),・・・・・,X(t),・・・・・

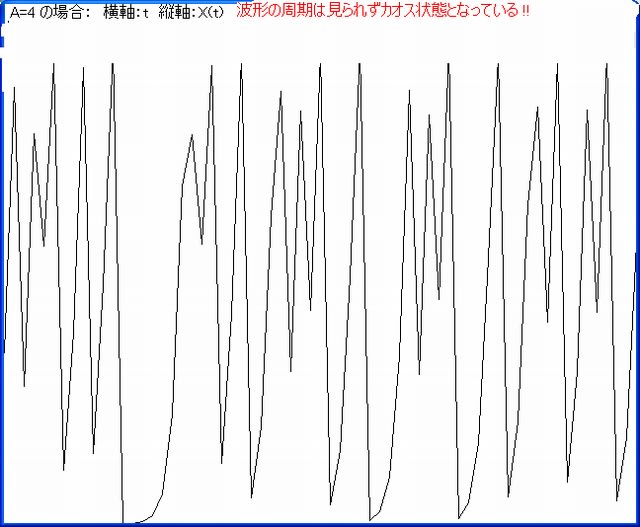
この数列がある値に収束するのか、発散するのか、振動するのか、あるいはカオス状態になるのかは記事m275で見てきた。　その画像を再び下に示す。



上図は t が充分大きいときの漸化値であるが、
X(0),X(1),X(2),X(3),・・・・・,X(t),・・・・・
全てを表示したらどうなるだろうか。それは、A が与えられた時の漸化の様子を示す画像となる。

下図は、X(0),X(1),X(2),X(3),・・・・・,X(t),・・・・・,X(500)-----------------(1)
ときの図である。



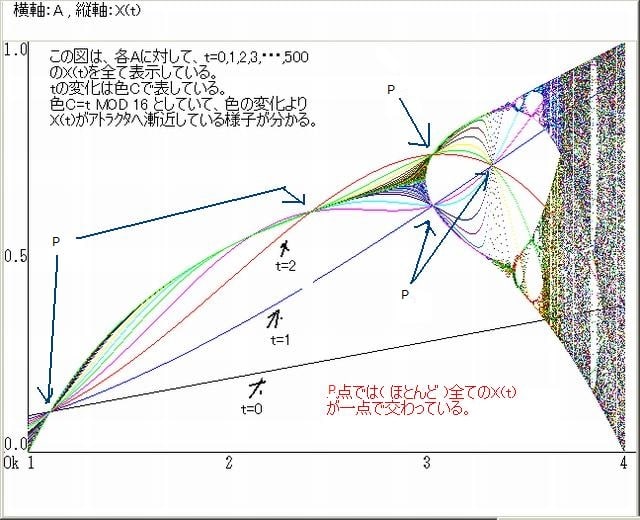
上図で、t の値は色で区別している。t=0,1,2,3,・・・,500　としている。
BASIC/98 では下図に示すように16色しか使えず、色にはパレット番号が付けられている。
そこで、t の区別は、パレットNo.C=t MOD 16 として区別した。



従って、色から、上記数列のアトラクタへの接近の様子が分かる。

この漸化の様子も、図の横軸：Aに対して、ある種の規則性がありそうだ。
例えば、図中のP点のように、上記(1)の全ての数列の値が一点で交わるようなA点が存在している。これは別の意味でのアトラクタと言えるのではないか？　詳細に調べると、この図には、いろいろな規則性があるようだ。

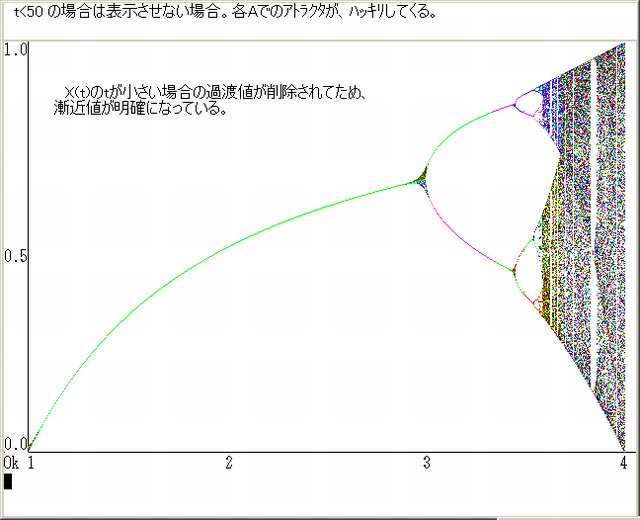
下図は、t が、ある値以下のX(t)は表示させない場合の図である。
上の図から、t を 50,100,400 以下のX(t)を表示させない図である。
順次、数列{X(t)}の過渡値が削除されめため漸近値(アトラクタ)が明確になっていく。但し、カオス状態は変わらない。








--------------------------------------------------------
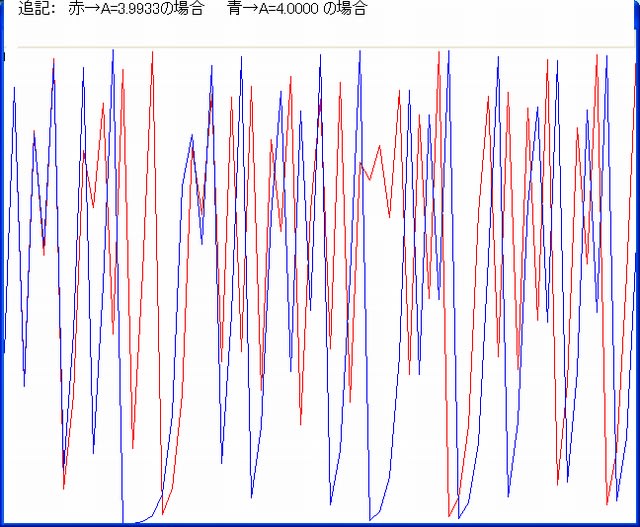
以下は、A=3.5～4の場合の画像である。
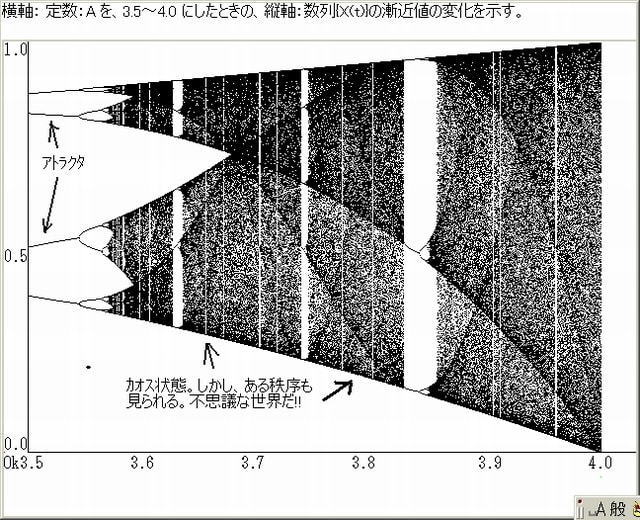
下図は記事274で示したアトラクタ及びカオスの画像である。



下図は、t=0,1,2,3,・・・,500 の全てのX(t)を表示した図である。
上のA=1～4図同様に、上記(1)の( ほとんど )全ての数列の値が或る一点 P に交わるような A 点が存在する。



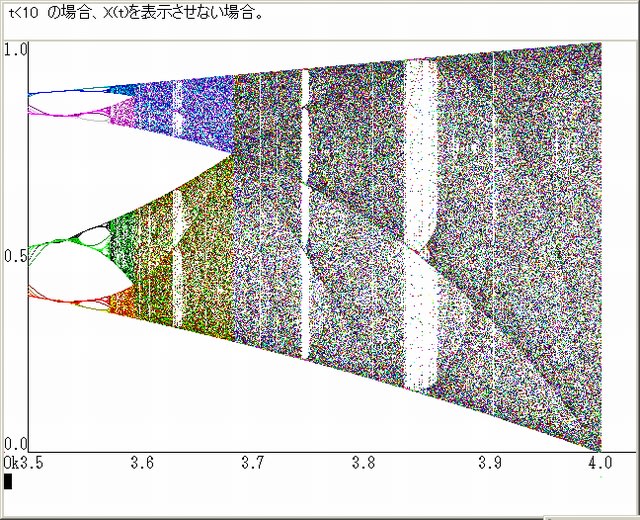
下図は、t が、ある値以下のX(t)は表示させない場合の図である。数列{X(t)}の過渡値が削除されめため漸近値(アトラクタ)が明確になっていく。

275 ヴエルンハルスト方程式画像(その2)

記事274にヴエルンハルスト方程式：X(t+1)=AX(t){1-X(t)}　・・・・・(1)
(ここで、A は定数、X(t)は変数)
画像を掲載した。
これはtの漸化式であるが、X(t)の漸化値が定数Aによって様相が一変することを見た。
A の増加に従い、X(t)の漸化値は、ある固定値から始まり分岐する。
その分岐は更に分岐し続け、あるA値からX(t)の値はカオス状態に突入したのであった。
下図は記事274に掲載した、その様子を示す画像である。



では、ヴエルンハルスト方程式(1)式において、Aを固定して、横軸にtをとり、
縦軸にX(t)にとって、t の変化に対してX(t)はどのように変化するのだろうか?
それを調べたのが下図である。A の代表的に四つの値で見てみよう。
A=2, A=3.3, A=3.5とA=4の場合である。
各場合の画像を以下に示す。









上図から分かるように一番上の画像と、A=2, A=3.3, A=3.5とA=4を固定した t 対 X(t)画像は
一致している。当然のことだが、A=4の場合のX(t)のカオス画像の様子は面白い。
なるほど、X(t)はtに対して予想不可能に見える。

---------------------------------------
追記：

274 ヴェルンハルスト方程式画像(その1)カオス画像の神秘さ

カオス関連の一般読者向けの本には恐らく必ず出てくるものに、ヴェルンハルスト方程式というものがある。これは中学生でも分かる以下の式だ。

X(t+1)=AX(t){1-X(t)} (ここで、A は定数、X(t)は変数)

これは漸化式で、X(t)が与えられた時、上式の右辺よりX(t+1)が求められるが、今度そのX(t+1)を上式の右辺のX(t)に置き換えて新しいX(t+1)を求める。
この操作を繰り返すことによって下式の数列が得られる。

X(0),X(1),X(2),・・・・,X(t),X(t+1),・・・・

この数列は際限なく単純に増加していったり、あるいは際限なく減少していったり、あるいは上がったり下がったりして振動して、ともかく、ある特定の値に漸近したり、振動したりする・・・と、フツーの人(勿論、私も含めて)思うだろう。

こんな単純な式には何の変哲もない退屈なコトしか無いだろう、と思うのが人情というものだ。

ところが、だ。知っている人には釈迦に説法だが、この単純極まりない式には、トンデモナイことが実は潜んでいるのだ。

確かに、この式は何の変哲もないコトから始まるのだが、ある時、突然、奇っ怪なことが突然始まるのだ。その奇っ怪なこととは、今や日常語にもなった『カオス』のことだが、つまり、『次に何が起こるか予想が付かない』が発生するのだ。

この現象を見事に目の当りに見せてくれる画像がある。
実は、この画像は今やよく知られた画像だが、私は自分で(プログラムを作ってみて)体験してみた。PC の画面に徐々に現れる、その画像を見ていると、その奇っ怪さが身にしみてくる。( 何事も自身で体験してみなければワカラナイことは世の中には多い。
この体験もその一つだろう。)

その奇っ怪な画像とは下に添付した画像だが、この画像の縦軸は数列{X(t)}の漸化値で(但し1に規格化してある)、横軸は定数 A だ。

A がある値までは何事もなく漸化値(アトラクタと呼ばれる)は単調に増加していくのだが、A=3あたりになると、アトラクタは二つに分岐する。つまり、数列{X(t)}の漸化値は、二つの値を行ったり来たりする。そしてAが増加すると更に分岐が始まる。更に又この分岐が急速に進み、ついにカオス状態へ突入していく。

カオス状態では『数列{X(t)}の漸化値』は予測不能な状態となる。

しかし不思議なことに、このカオス状態の画像をよく見ると、ある種の秩序がある
ことが分かる。カオスの画像の濃淡の中にある複雑な放射線状のモノがそれだ。
そして更によく見ると、このカオス画像はフラクタル性(自己同一性)もある。

こんな簡単な式(ヴェルンハルスト方程式)に、一体、何ゆえに、このような複雑さ・豊穣さが
潜んでいるのだろう!!!??? 不思議とは、こういうことだ。

実は、この画像のカオス性は数学の単なるお遊びではなくて、この世の森羅万象のには、よく見られる現象なのだ。

ここらの話の本はたくさんあるだろうが、私のお気に入りの本を紹介しておこう。
これも古い本だ。『鏡の伝説--カオス-フラクタル理論が自然を見る目を変えた』(J.ブリッグス、F.D.ピート著、ダイヤモンド社)。