300 Z^2マンデルブロ集合画像とブッダブロ集合画像を重ねた画像

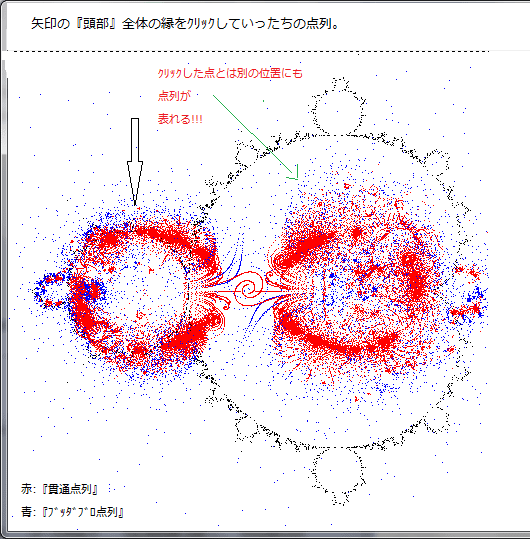
下図はZ^2マンデルブロ集合画像の近似境界(赤線)と、記事294の最後のブッダブロ集合画像を重ね合わせた画像である。それらの画像の位置関係が分かる。

(注：『記事294の最後のブッダブロ集合画像』は、Z^2マンデルブロ集合内の全ての点を始点とした場合のlog画像である。詳細は記事294を参照。)

291 マウスのクリック点での点列画像(その2)

マンデルブロ集合画像の縁(ふち)をマウススでクリックして始点を与えた場合の、『貫通点列』(赤色)と『ブッダブロ点列』(青色]の他の画像例を以下に示す。クリックした点とは全く別の位置に点列が現れる場合がある。







上の画像でも分かるように、マンデルブロ集合画像の『頭部』周辺に『貫通点列』が多く現れることが分かる。この場合でも、『頭部』周辺をクリックして始点にしたにも関わらず、全く別の個所(『腹部』にも同時に点列が現れる。

***
実は、画像の参照として表示したマンデルブロ集合の縁(ふち)は、マンデルブロ集合の真の境界ではない。真の境界よりもが外部の点なのである。現在、調査中であるが、真の境界より少しでも外部に外れた点は、『ブッダブロ点列』となるらしい。また少しでも、真の境界より内部に
ずれた始点のみが『貫通点列』となるらしい
。
***
これは当然なことに思えるが、現在、調査中のプログラム実行結果はこのことを明確に示した結果となっている。

289 マウスをクリックして始点を選ぶ方法

ブッダブロ点列 (巡回ループを脱出した時点で過去全ての点列)と貫通点列 (巡回ループを脱出できず貫通した時点で過去全ての点列)の画像作成時の始点は、いままで乱数を使うか、あるいは表示座標を全て順次与えていく方法であった。

***
この方法では調べたい点での、それらの点列の様子を調べるには不便であり、始点と、点列の関係もよく分からない。

そこで、あらかじめマンデルブロ集合の縁(ふち)を表示しておき、その縁ないしマンデルブロ集合内部の点を、マウスを使って自由に選び、その点での点列を表示させるプログラムを作った。

***
以下の画像は、そのプログラムによる点列画像である。
表示範囲は実軸:-1.5＜X＜0.5,虚軸:-1＜Y＜1である。最大巡回回数は500とした。
赤色の点列は貫通点列で、青色の点列はブッダブロ点列である。









-----------------------------------------------------------
この方法で分かったことは、マウスでクリックした点とは全く別の座標に点列が
表れる場合が多いということ。

***
当然なことではあるが、マンデルブロ集合部ではブッダブロ点列を生成する始点よりも、貫通点列を生成する始点のほうが圧倒的に多いということ。

そもそも、マンデルブロ画像の内部ないし縁(ふち)は、巡回ループを脱出しない点、ないしは巡ループを脱出するのに巡回回数が無限大となる点の集合だから、ループを貫通してしまうのは当然である。即ち、貫通点列となるのは当然である。

***
しかし、たまにはブッダブロ点列を生成する点もある。比較的に、それが多いのは上図の最後の画像で示しているように、マンデ゛ルブロ集合の『尻』の辺りの点である。理由はよく分からない。

***
参考に、BASIC/98で作った、このプログラムを下記しておく。

10 REM 始点をマウスで入力:マンデルブロ+ブッダブロの点列の表示
90 REM 始点のマウス入力はマウスの左ボタンをクリック。
110 REM 始点の入力の終わりにはキーF1を押す。行82
130 REM 表示座標点→行112,114
150 REM 表示座標→行250,270:変えた場合はマンデルブロ集合画像の縁(ふち)画像も変えること。
190 CONSOLE ,,0,1
210 COLOR 0,7,,,2
230 CLS 3
250 CXS=-1.5:CXE=0.5:DX=(CXE-CXS)/480
270 CYS=-1:CYE=1:DY=(CYE-CYS)/480
290 I=0:II=0:N1=0:NN=0
294 DIM SX(10000):DIM SY(10000)
330 CHAIN MERGE "C:\BASIC1\PRO\SUBR\ER2.BAS",350,ALL
350 ON ERROR GOTO 50000
370 REM マンデルブロ集合の縁(ふち)の表示
390 OPEN "C:\BASIC1\TEST\DATAマンデルA.DAT" FOR INPUT AS #1
410 INPUT #1,K,J,C
430 IF EOF(1) THEN 490
450 PSET (K,J),0
470 GOTO 410
490 CLOSE #1
492 ON KEY GOSUB *KEY1
494 KEY(1) ON
500 ON MOUSE(2) GOSUB *M1
510 MOUSE (2) ON
520 '
530 DO:AA=AA:LOOP
540 '
550 *M1
560 A=MOUSE(4,1):B=MOUSE(5,1)
570 CX=CXS+DX*A
580 CY=CYS+DY*B
610 PSET (A,B),2
620 GOSUB 1270
650 RETURN
1270 REM 画像の作成
1290 L=0
1330 K=0:J=0
1410 REM N-loopの計算
1430 X=0:Y=0
1450 FOR N=0 TO 500
1470 XX=X^2-Y^2+CX
1490 Y=2*X*Y+CY
1510 X=XX
1530 Q=X^2+Y^2
1550 SX(L)=X: SY(L)=Y
1570 IF Q>4 THEN 1900
1610 L=L+1
1630 NEXT N
1634 FOR N=0 TO 500
1750 X=SX(N):Y=SY(N)
1770 K1=(X-CXS)/DX : J1=(Y-CYS)/DY
1790 IF K1<0 OR J1<0 THEN 1910
1810 IF K1>480 OR J1>480 THEN 1910
1830 K=INT(K1) : J=INT(J1)
1852 PSET (K,J),2
1853 NEXT N
1858 GOTO 2020
1900 REM N-loop脱出後
1910 FOR LL=0 TO L
1920 X=SX(LL):Y=SY(LL)
1930 KK=(X-CXS)/DX : JJ=(Y-CYS)/DY
1940 IF KK<0 OR JJ<0 THEN 2000
1950 IF KK>480 OR JJ>480 THEN 2000
1960 K=INT(KK) : J=INT(JJ)
1970 C= M MOD 16
1980 PSET (K,J),1
2000 NEXT LL
2010 L=0
2020 RETURN
2030 *KEY1
2040 LINE(0,0)-(480,0),0,,2
2050 END

287 ブッダブロ画像作成時の点列の画像

ブッダブロ画像は、巡回ループを脱出する点Zn(X,Y)があったとき、その点の過去の点、即ち、Z0,Z1,Z2,・・・,Znを全て表示する画像であった。この場合、始点Z0は任意の点として与えられる。

***
以下の図は、画像表示範囲を実軸:|X|＜2,虚軸:|Y|＜2としたとき、任意の始点Z0を500個与えたときの、点列Z0,Z1,Z2,・・・,Znの画像である。参照のため、マンデルブロ集合の縁(ふち)も同一座標で表示している。

***
以下の画像から分かるように、点列が形成されるのは、始点Z0がマンデルブロ集合付近内に限ることが分かる。他の始点の場合は一点Z0で巡回ループを脱出してしまい点列が形成されず、画像の中に孤立した点として残っている。

***
同じ始点から出来る点列は同じ色にしている。但し、色は15色しか使えないから、与える始点の順序をMとすると、色C=M MOD 16としている。

***
点列が形成されるとき、与えられた始点Z0の位置によって、点列の形が
変化している。その形はそれぞれ個性的で面白い。

282乱数を使ったブッタブロ画像(その2)

乱数を使わないブッダブロ画像については前記事で調べてきた。
今回は、始点に乱数を使う本来の画像について再度試みた。(記事277も乱数を使っている)

Wikipedia掲載の簡単な解説に従って、BASIC/98でプログラミングしているのだが、今回、巡回回数を21万回(記事277では10万回)の画像を作ったが、どうもWikipedia掲載の画像のような画像が得られない。尤も、BASIC/98では色の濃淡が表現できず、16色の色でしか濃度：mを表せないから、その点が画像の微細な表現が出来ないのは仕方ない。

***
下図は今回作った画像の中央部を縦に切ったときのm( 正確には、2*LOG(m) )の分布図である。mのダイナミックレンジは、0～2*LOG(m)=15以上、即ち、m は 0 からe^15/2=1808以上もある。この図を、よく見ると、画像を構成しているmは、0から約1800以上の間に散在している。この散在したmの分布を16色で表現しようとすること自体無理があり、画像の微細さが表現できないのは当然と言える。



下図は、C=2*LOG(m)の画像である。巡回回数は21万回で、Nmax=500とした。



BASIC/98の色コードは、8以上は簡単には区別できない色で構成されているる。
そこで比較的区別しやすい、0～7のみ使用するため、C=2*LOG(m) MOD 7 とした画像が下図である。



これらの画像において、画像の微細さが表現できないのは、使用ツール(BASIC/98)の限界に依るのは仕方ないとしても、ちょっと理解できないのは、Wikipedia掲載の画像と根本のところで異なっているように見えることだ。

むしろ、前回の乱数を使用しない方法の画像(記事277の画像)のほうが、Wikipedia掲載の画像に近い。それらの画像で異なる点は始点の与え方のみであり、他の計算手順は全く同じである。

***
今回の画像において、乱数の与え方に問題があるのだろうか?

今回の画像において前回同様に、乱数はRND コマンドを使い、始点Z(X,Y)は、画像表示範囲を
Xs～Xe,Ys～Yeとすると、X=(Xe-Xs)RND-Xs,Y-(Ye-Ys)RND-Ys とした。

***
参考のために、BASIC/98での画像作成と表示のプログラムを以下に掲載しておく。

10 REM ブッダブロ画像作成プログラム
110 CONSOLE ,,0,1
120 COLOR 0,7,,,2
130 CLS 3
140 '
144 RANDOMIZE 50
180 CXS=-1.4 :CXE=0.6 :DX=(CXE-CXS)/480
190 CYS=-1 :CYE=1 :DY=(CYE-CYS)/480
200 M=1 :L=0
202 DIM Z(480,480):DIM SX(10000):DIM SY(10000)
204 FOR J=0 TO 480
206 FOR K=0 TO 480
208 Z(K,J)=0
210 NEXT K,J
212 K=0:J=0
228 OPEN "C:\BASIC1\TEST\DATA.DAT" FOR OUTPUT AS #3
248 REM CX,CY given
250 CY=2*RND-1
260 CX=2*RND-1.4
262 REM M:最大反復回数
264 IF M=1.2*10^6 THEN 600
266 LOCATE 0,0:PRINT M
270 X=0:Y=0
288 FOR N=1 TO 500
290 XX=X^2-Y^2+CX
300 Y=2*X*Y+CY
310 X=XX
320 Q=X^2+Y^2
324 IF Q>4 THEN 400
328 SX(L)=X: SY(L)=Y
330 L=L+1
340 NEXT N
350 GOTO 248
400 REM
411 IF N=1 THEN 590
420 FOR LL=0 TO L
422 X=SX(LL):Y=SY(LL)
444 KK=(X-CXS)/DX : JJ=(Y-CYS)/DY
445 IF KK<0 OR JJ<0 THEN 460
446 IF KK>480 OR JJ>480 THEN 460
448 K=INT(KK) : J=INT(JJ)
450 Z(K,J)=Z(K,J)+1
452 C= N MOD 16
454 PSET (K,J),C
460 NEXT LL
464 L=0
590 M=M+1:GOTO 248
600 REM DATA FILE の作成
610 FOR JJJ=0 TO 480
620 FOR KKK=0 TO 480
630 IF Z(KKK,JJJ)=0 THEN 650
640 WRITE #3,KKK,JJJ,Z(KKK,JJJ)
650 NEXT KKK
660 NEXT JJJ
670 END
*****************
10 REM ブッダブロ表示(K,J,Zmax)デタの表示プログラム
30 CONSOLE ,,0,1
40 COLOR 0,7,,,2
50 CLS 3
58 OPEN "C:\BASIC1\TEST\DATA.DAT" FOR INPUT AS #1
60 INPUT #1,K,J,Z
70 IF EOF(1) THEN 120
80 REM Zによる色の区別：サブルーチン
90 GOSUB 1000
100 PSET (J,K),C
110 GOTO 60
120 CLOSE #1
140 END
1000 REM Zによる色の区別
1010 IF Z=0 THEN 2000
1020 C=2*LOG(Z)
2000 RETURN

281 乱数を使わないブッダブロ画像(その4)

今回は、前記事のデータにおいて、濃度mをlog化した画像を作成する。
ここで注意すべき点は、BASIC/98でのPSET(K,J),C コマンドにおける C の取扱いである。C 最終的には正整数となるが、最初から C=INT(LOG(m))とすると画像データの損失を招く。C=LOG(m)としておいたほうが良い。




下図は、C=2*LOG(m)の分布図である。この図より、C=2*LOG(m)にしてもC値の飽和を招ず、C=LOG(m)より大きく、Cのダイナミック・レンジがとれる。




下図は、C=LOG(m) と　C=2*LOG(m)　の全データを、そのまま使用した画像である。
よく見ると分かるが、C=LOG(m)画像よりも、C=2*LOG(m)画像のほうが、より多い色で構成されている。これは、C のダイナミック・レンジが大きくなった効果である。





下図は、C=2*LOG(m)画像を適当に画像処理にしたものである。
単純な画像処理であるが、ボンヤリとではあるが座禅した仏像の姿が見えてきて面白い。私は画像処理の技術の知識は皆無であるが、簡単なことは出来そうだ。例えば、1ピクセルだけ孤立している点は簡単なプログラムで除去できそうだ。

280 乱数を使わないブッダブロ画像(その3)

今回の画像は前回の画像でのブッダブロ画像(座禅した仏像を擬した画像)部分を拡大したものである。画像の縦軸は、-1.5～0.5cm。横軸は、-1～+1cmである。

279 乱数を使わないブッダブロ画像(その2)

前記事278では、画像表現にlog(m)を使用した。

複素平面の画像作成の始点Z(X,iY)に乱数を使用しない方法( 即ち、画像表示座標の横軸及び縦軸を順次、始点にしていく方法 )では、同一座標点となる個数( これを濃度と定義し、m で表わす )の最大数は13であった。(但し、ブッダブロ画像そのものに寄与しない
特異点は約50以上の点があったが、それらは無視した。)

****
mの最大値が13程度ならば、BASIC/98の16色で表現可能であるが、しかし、ブッダブロ画像自体にハッキリとしたmの規則性が見られず、そのままのデータを直接、色表示したのでは画像構造がハッキリと分からない。

****
その構造をハッキリさせる方法は、log(m)による画像表現も其の一つだが、生(なま)データを、より直接に使う方法：C=mについて今回は調べてみた。以下は、その検討結果である。









(訂正：下図の画像の縦軸は、|X|＜1cm,横軸は、-1.5cm＜Y＜0.5cm)

278 乱数を使わないブッダブロ画像(その1)

ブッダブロ画像は点(CX,CY)を新たに選ぶ場合、乱数を使用していたが、乱数は使わず、画像表示画面の全てを順次選ぶ場合の画像を調べてみる。
****
表示ガウス画面の座標(X,iY)を|X|＜=2,|Y|＜=2とする。

X,Yをパラメータ K,Jで表し、X=Xs+dX*K,Y=Ys=dY*J とし、dX=dY=4/480,K=0～480 step1,J=0～480 step 1とする。

画像作成での始点：Z(X,Y)をZ(K,J)として、K=0→480,J=0→480 全てについて順次与えて画像を作成していく。画像作成手順は、始点Zの与え方以外は全て同じである。但し、巡回ループの最大値は500としている。
****
また、同一点の重なりの回数(以下、濃度：mと表現する)は色で表現する。
(BASIC/98では、mを同一色のグラディエーションでは表現できず、最大16色の色でしか表せない。)

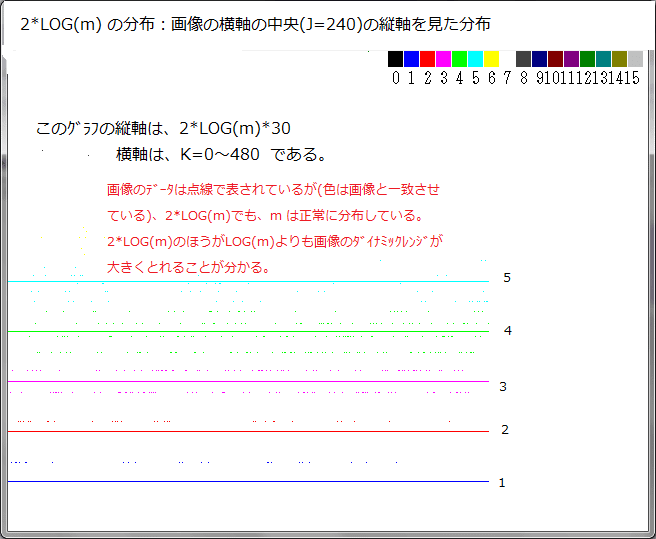
下図は、ブッダブロ画像において、J=480/2の場合のK=0→480でのmの分布を調べたグラフである。m の最大値は13となっている。



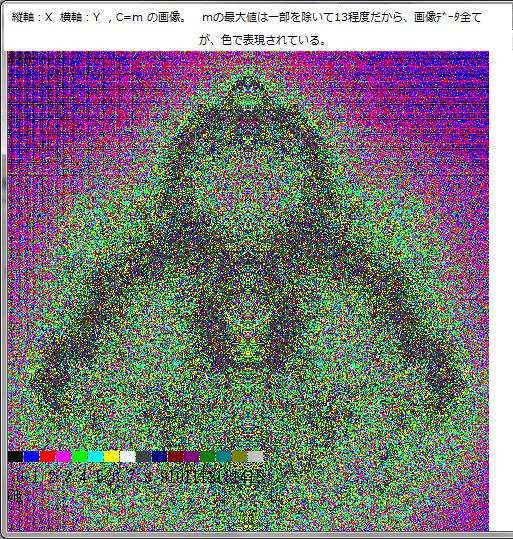
下図は、この方法で求めたブッダブロの生(なま)の画像である。但し、周囲の部分は省略し肝心の部分のみ示した。

C=m MOD 16　としているが、m の最大値は13だから、C=mとしてみてよい。

この図から分かるように、ブッダブロ画像のmの分布は混在しており、明確な規則性はない(これは、色が混在しており不鮮明であることから分かる)。

(訂正：下図の画像の縦軸は、-1cm～1cm,横軸は、-1.5cm～0.5cmである)



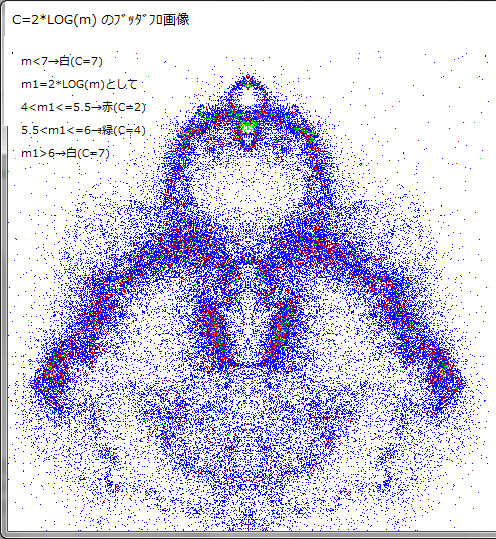
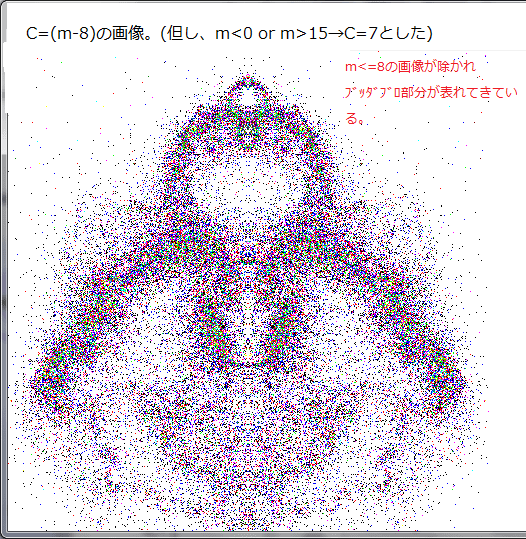
上の画像は生(なま)データを直接表示したものであるが、画像の色(即ち m )を整理する方法として、log(m)化がある。以下の画像は、log(m)にして、不要な　m を未表示にした画像である。画像表示の具体的な方法は各画像に書いてある。

これらの画像は、いわゆるブッダブロ画像と似ている。尚、下図の画像は、色のみ変えており画像の形態は同じである。







-------------------------------------------------------

参考のために上の画像のBASIC/98プログラムを下記しておく。

画像作成プログラム(BASIC/98)
10 REM ブッダブローFILE NAME→ KL
20 REM CX,CY→K,L
60 CHAIN MERGE "C:\BASIC1\PRO\SUBR\KOSHIKI.BAS",90,ALL
90 CHAIN MERGE "C:\BASIC1\PRO\SUBR\ER2.BAS",100,ALL
100 ON ERROR GOTO 50000
110 CONSOLE ,,0,1
120 COLOR 0,7,,,2
130 CLS 3
140 GOSUB 10000
180 CXS=-2 :CXE=2 :DX=(CXE-CXS)/480
190 CYS=-2 :CYE=2 :DY=(CYE-CYS)/480
200 DIM Z(480,480):DIM SX(10000):DIM SY(10000)
202 FOR J=0 TO 480
204 FOR K=0 TO 480
206 Z(K,J)=0
208 NEXT K
210 NEXT J
220 K=0:J=0:N=1:L=0
228 '
232 REM Jの値
240 LOCATE 0,0:PRINT J
250 CY=CYS+DY*J
260 REM Kの値
262 LOCATE 0,1:PRINT K
264 CX=CXS+DX*K
270 X=0:Y=0
288 REM
290 XX=FNR2(X,Y)+CX
300 Y=FNI2(X,Y)+CY
310 X=XX
320 Q=X^2+Y^2
324 IF Q>4 THEN 1000
330 SX(L)=X :SY(L)=Y
334 L=L+1
340 IF N=500 THEN 341 ELSE N=N+1:GOTO 288
341 N=0
350 REM J,Kの値の判定
360 IF K=480 THEN 400 ELSE 370
370 K=K+1
380 L=0: GOTO 260
400 IF J=480 THEN 1500 ELSE 410
410 K=0:J=J+1
420 L=0: GOTO 232
1000 REM X→SX(L),Y→SY(L)の読み込み
1420 FOR LL=0 TO L
1422 X=SX(LL):Y=SY(LL)
1444 KK1=(X+2)/DX : JJ1=(Y+2)/DY
1446 K1=INT(KK1) : J1=INT(JJ1)
1448 IF K1 1449 IF K1>480 OR J1>480 THEN 1460
1450 Z(K1,J1)=Z(K1,J1)+1
1454 C=N MOD 16
1457 PSET (K1,J1),C
1460 NEXT LL
1462 L=0:N=0
1464 GOTO 350
1500 REM ZZ=Z(K1,J1) の書き込み
1502 OPEN "C:\BASIC1\TEST\DATAb.DAT" FOR OUTPUT AS #1
1504 FOR JJJ=0 TO 480
1506 FOR KKK=0 TO 480
1508 WRITE #1,JJJ,KKK,Z(KKK,JJJ)
1510 NEXT KKK
1512 NEXT JJJ
1514 CLOSE #1
1600 END
-----------------------------------
log(m)画像の表示プログラム(BASIC/98)
10 REM ブッダブロ表示(K,J,Zmax)デタの表示
12 REM Zmax値による色の区別はサブルーチン(1000行)で決める
30 CONSOLE ,,0,1
40 COLOR 0,7,,,2
50 CLS 3
51 CHAIN MERGE "C:\BASIC1\PRO\SUBR\COLOR左下表示.BAS",55,ALL
55 OPEN "C:\BASIC1\TEST\DATAb.DAT" FOR INPUT AS #1
60 INPUT #1,K,J,Z
62 LOCATE 0,0:PRINT USING "###";J
64 LOCATE 0,1:PRINT USING "###";K
70 IF EOF(1) THEN 120
72 '
74 '
80 REM Zによる色の区別：サブルーチン
90 GOSUB 500
100 PSET (K,J),C
110 GOTO 60
120 CLOSE #1
130 GOTO 600
500 REM Zによる色の区別
510 IF Z 520 CCC=LOG(Z)
522 IF CCC>2 AND CCC 524 C=CCC:GOTO 540
526 CC=LOG(Z)
528 IF CC>=2.5 THEN C=CC+5 ELSE C=7
540 RETURN
600 GOSUB 3000
610 END

277 ブッダブロもどき画像

ブッダブロ゛ー画像という画像がある。
ウィキペデイアによると、この画像は以下の画像のようである。

『ブッダブロ（英: buddhabrot）とはマンデルブロ集合に関する図形。ガウス平面から点cをランダムに選び、そのcについて数列z{n+1} = {zn}^2 + cを計算し、|z{n+1}|＞2となった場合にz1からznまでの位置に点を描くという作業を、指定した回数だけ反復（iteration）して行ったもの。形がブッダに似ていることから名付けられた。色毎に計算回数を変えてカラー化することもある。』

http://ja.wikipedia.org/wiki/%E3%83%96%E3%83%83%E3%83%80%E3%83%96%E3%83%AD

画像作成手順も以下のように書かれている。

『基本の計算にはマンデルブロ数列を用いる。まずガウス平面の内の実数部、虚数部それぞれ-2～2の範囲を描画面に見立て、描画点の細かさを決めておく。
次に描画面から点をランダムに選び、をから順に計算し、、|z{n+1}|＞2になった時点で（発散が明らかになった時点で）、描画面のからの位置に点を描く。すでに点が描いてあった場合には、より明るくする。（ただしの上限を決めておき、それ以上になったら収束したと見なして点は描かない。）次にまた新たなをランダムに決め、先の計算を反復する』

そこで私はBASIC/98で、この画像を求めてみることにした。
問題は、BASIC/98では、『すでに点が描いてあった場合には、より明るくする』便利な方法がないことだ (いや、あるかも知れないが残念ながら私は知らない。)

BASIC/98で決められた16色の色で表現するにはどうしたらよいか、が最大の問題である。
複素平面の一点が加算されるに従い、白色の色調を連続的に濃淡が可能ならば、この画像の作成自体は容易に思われる。

その点は棚明けして、とりあえず、16色でトライしてみることにした。
トライした計算手順は以下のとおりである。

****
プログラム A

1.ガウス平面からランダム点(CX,CY)を選ぶ。
2.マンデルブロ画像作成での巡回ループ(N-loop)で、X,Yの初期値を0として、Z(=X+iY)←Z(X+iY)+CX+iCY を巡回計算し、その都度点(X,Y)をDATAaにシークエンシャル保存する。X^2+Y^2>4になった時点でN-loopを脱出して、DATAaを読み出しDATAbに保存する。その場合、点(x,y)が読みだされたとき、Z(x,y)=Z(x,y)+1として、点(x,y)が読みだされた回数をZ(x,y)も保存していく。
3.M=M+1として、ランダム点(CX,CYの選択回数を記録し、1.の手順にもどり同じ計算をM=Mmaxになるまで繰り返す。N-loopを貫通した場合はMにカウントしない。

*****
プログラム　B

DATAbのシークエンシャル・ファイル(x,y,Z(x,y))の順に保存されてい)る)を読 みだして、Z(x,y)の最大値を求め、そのZ(x,y)max=ZZを(x,y,ZZ)として、DATAcにシークエンシャル保存する。

****
プログラム C

DATAcを読み出し、pset(x,y),ZZ　として表示する。その場合、ZZに適当な規則を与えて色で表現化する。

****
以上が私が作成したプログラム手順であるが、ここで、x,yは、それぞれ整数K,Jをパラメータとして表現する。今回の画像の場合、J=0～480,K=0～480としている。

以下の図は、M=100000、N=500 の場合の画像である。
この図の右側に、Z(x,y)maxの適当に区分けして、その中にある点(x,y)の数を→で示している。 このZ(x,y)maxの区分けは特別な意味はなく、とりあえず、この表のように区分けた。 この区分けの中に入る点(x,y)は同じ色で表現される。その点(x,y)の数が多い順に、その点の色は単純に16色コード順にした。 このZ(x,y)maxの区分けによる色の単純化が画像の情報の損失となり画像が単純化されている。　この点、Z(x,y)maxを黒白の濃淡として表現されている。 ウィキペディア掲載の画像に比べ粗雑であるが、なんとなく全体像は似ている。



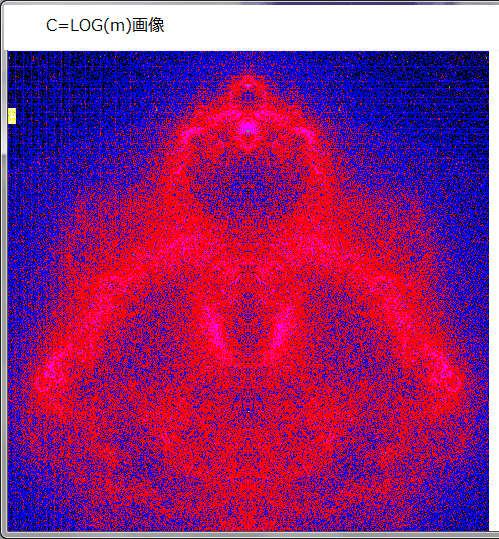
下図は、DATAcに保存された全てのデータにおいて、点(x,y)の色：Cを、C=int(log((Z(x,y)max))とした画像である。ここで、Z(x,y)max=0の場合は、色は白としていて画像には表示されない。　また、C=7(白)の場合は C=15 としたが、特別な理由はない。
このlog画像は全データを使用しているという意味では連続的であるが、log化による色の単純化が行われており、その点、画像が粗雑となっている。



以上が私の『ブッダブロ画像』であるが、上記したように、かなり粗雑化が行われており、『ブッダブロもどき画像』と言ったほうがよい。しかし、これはこれで結構楽しい画像ではある。また以上の画像で横軸はyで縦軸はxである。

---------------------------------------
下図は上記プログラム A で、M=100,Nmax=500とした場合の、N-loop脱出前の点：(x,y)の表で、色：C　は、N-loop脱出時のNをNoとしたとき、C=No MOD 16としている。
この図を見ていると、N-loop脱出前の点：(x,y)の軌跡が色として推定できて面白い。
渦状になったり、花火風に散っていったり、様々な形状をしていくのが見えて楽しい。



下図は、M=100000、Nmax=500の場合の上図である。
こうなると複雑で何が何だか分からないが、なんとなく、ブッダブロ画像が潜んでいる
感じはする。但し、この図の横軸はx、縦軸はyである。




------------------------------------------------------------
以下参考に、私が作成したBASIC/98のプログラムを下記しておく。
これらのプログラムには直接関係のないコマンドも含まれているが面倒だから、そのままにしてある。このプログラムで少し気になっているのはプログラムAでの、RNDの使い方である。　
*******************
プログラ A
----------------------------------
10 REM ブッダブロー
20 REM CX,CY→RND
60 CHAIN MERGE "C:\BASIC1\PRO\SUBR\KOSHIKI.BAS",90,ALL
90 CHAIN MERGE "C:\BASIC1\PRO\SUBR\ER2.BAS",100,ALL
100 ON ERROR GOTO 50000
110 CONSOLE ,,0,1
120 COLOR 0,7,,,2
130 CLS 3
140 GOSUB 10000
180 CXS=-2 :CXE=2 :DX=(CXE-CXS)/480
190 CYS=-2 :CYE=2 :DY=(CYE-CYS)/480
200 M=1 :DIM Z(480,480)
202 FOR J=0 TO 480
204 FOR K=0 TO 480
206 Z(K,J)=0
208 NEXT K
210 NEXT J
228 OPEN "C:\BASIC1\TEST\DATAb.DAT" FOR OUTPUT AS #3
230 OPEN "C:\BASIC1\TEST\DATAa.DAT" FOR OUTPUT AS #1
248 REM CX,CY given
250 CX1=RND :CX2=RND:CX=(CX1-CX2)*2
260 CY1=RND :CY2=RND:CY=(CY1-CY2)*2
264 IF M=100000 THEN END
266 LOCATE 0,0:PRINT M
270 X=0:Y=0
288 FOR N=1 TO 500
290 XX=FNR2(X,Y)+CX
300 Y=FNI2(X,Y)+CY
310 X=XX
320 Q=X^2+Y^2
324 IF Q>4 THEN 400
325 '
330 WRITE #1,X,Y,C
340 NEXT N
350 GOTO 248
400 CLOSE #1
410 OPEN "C:\BASIC1\TEST\DATAa.DAT" FOR INPUT AS #2
411 IF N=1 THEN 470
420 INPUT #2,X,Y,C
440 IF EOF(2) THEN 470
442 C=N MOD 16
444 KK=(X+2)/DX : JJ=(Y+2)/DY
446 K=INT(KK) : J=INT(JJ)
450 Z(K,J)=Z(K,J)+1
452 ZZ=Z(K,J)
457 PSET (K,J),C
458 WRITE #3,K,J,ZZ
460 GOTO 420
470 CLOSE #2
580 KILL "C:\BASIC1\TEST\DATAa.DAT"
590 M=M+1:GOTO 230
*****************
プログラム B
--------------------------------------------
10 REM DATAbの(K,J,Z)デタを(K,J,Zmax)に並び変えて、それを
20 REM DATAcとして保存する。
30 CONSOLE ,,0,1
40 COLOR 0,7,,,2
50 CLS 3
60 DIM Z(480,480)
70 FOR J=0 TO 480
80 FOR K=0 TO 480
90 Z(K,J)=0
100 NEXT K
110 NEXT J
120 OPEN "C:\BASIC1\TEST\DATAb.DAT" FOR INPUT AS #1
130 INPUT #1,K,J,Z
140 IF EOF(1) THEN 180
150 IF Z>Z(K,J) THEN Z(K,J)=Z
160 N=N+1:LOCATE 0,0:PRINT N
170 GOTO 130
180 CLOSE #1
190 REM 変換されたデタの保管→DATAc
200 OPEN "C:\BASIC1\TEST\DATAc.DAT" FOR OUTPUT AS #2
210 FOR J=0 TO 480
220 LOCATE 0,2:PRINT J
230 FOR K=0 TO 480
240 ZZ=Z(K,J)
250 WRITE #2,K,J,ZZ
260 NEXT K
270 NEXT J
280 CLOSE #2
290 END
********************
プログラム C
--------------------------------
10 REM ブッダブロ表示(K,J,Zmax)デタの表示
12 REM Zmax値による色の区別はサブルーチン(1000行)で決める
30 CONSOLE ,,0,1
40 COLOR 0,7,,,2
50 CLS 3
51 '
55 OPEN "C:\BASIC1\TEST\DATAc.DAT" FOR INPUT AS #1
60 INPUT #1,K,J,Z
62 LOCATE 0,0:PRINT USING "###";J
64 LOCATE 0,1:PRINT USING "###";K
70 IF EOF(1) THEN 120
72 '
74 '
80 REM Zによる色の区別：サブルーチン
90 GOSUB 1000
100 PSET (J,K),C
110 GOTO 60
120 CLOSE #1
130 GOTO 3000
1000 REM Zによる色の区別
1010 IF Z 1020 IF Z>51 AND Z 1030 IF Z>101 AND Z 1040 IF Z>201 AND Z 1050 IF Z>301 AND Z 1060 IF Z>401 AND Z 1070 IF Z>501 AND Z 1080 IF Z>601 AND Z 1090 IF Z>701 AND Z 1100 IF Z>801 AND Z 1120 IF Z>901 AND Z 1130 IF Z>1001 AND Z 1140 IF Z>2001 AND Z 1150 IF Z>3001 AND Z 1160 IF Z>4001 AND Z 1170 IF Z>5001 AND Z 1180 IF Z>6001 THEN C=15
2000 RETURN
3000 REM 5本ずつ同色にして、色の判定 file name COMMOM\色3
3050 C=0:D=0:DD=375
3060 FOR K=0 TO 14
3070 LINE (K+D+DD,400)-(K+D+DD,410),C
3080 NEXT K
3090 D=D+16
3100 C=C+1
3110 IF C=16 THEN 3140 ELSE 3060
3140 LOCATE 47,23:PRINT " 0"
3142 LOCATE 49,23:PRINT " 1"
3143 LOCATE 51,23:PRINT " 2"
3145 LOCATE 53,23:PRINT " 3"
3146 LOCATE 55,23:PRINT " 4"
3147 LOCATE 57,23:PRINT " 5"
3148 LOCATE 59,23:PRINT " 6"
3149 LOCATE 61,23:PRINT " 7"
3150 LOCATE 63,23:PRINT " 8"
3151 LOCATE 65,23:PRINT " 9"
3152 LOCATE 67,23:PRINT "10"
3153 LOCATE 69,23:PRINT "11"
3154 LOCATE 71,23:PRINT "12"
3155 LOCATE 73,23:PRINT "13"
3156 LOCATE 75,23:PRINT "14"
3157 LOCATE 77,23:PRINT "15"
3167 LOCATE 0,24
3200 END