アゼルバイジャン語(Azerbaijani) Həqiqi paraleloqrafik problem (MIYA problemi)

アゼルバイジャン語(Azerbaijani)

Həqiqi paraleloqrafik problem (MIYA problemi)
     S.Miyazaki (13 noyabr, 2017)
Bu 1922-ci ildə ibtidai geometriyada "Langley problemi" nin inkişaf etmiş bir versiyasıdır.
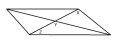
Dörd üçbucaqlı paraleloqram şəklində göstərildiyi kimi, X, Y və Z açıları ilə xarakterizə olunur. Dörd üçbucaqlı paraleloqramda, kənar və diaqonallardan yaranan hər bir açı bu dərəcədə tam dəyərə malikdir, burada "tam bərabərlikli paraleloqram" deyilir.
İçərədəki üçbucaqların tam, X, Y və Z tam ədədi dəyərlərini verən bir "paraleloqram tam ədədi ilə" mövcud olduğunu sübut edin.
Burada qeyri-ağır həllər üzündən rombozlar (Y = 90 °), kvadratlar və düzbucaqlılar (X + Z = 90 °) kimi xüsusi paraleloqrafik halları istisna edirik.
Bundan başqa, biz paraleloqram və onun aynası simmetriya forması / rotasiya simmetriyası şəklində fərqlənmirik.
(* Saito, H., "Başlanğıc geometriyada generalləşdirilmiş Langley problemləri üçün dəlilləri tapmaq" (WEB məqaləsinə baxın) (DRAFT20161211))