今、会社の業務で新人の同僚と筐体の音響伝達特性を評価中です。
伝達関数やFFTについて彼に教えています。
どんどん知識を吸収してくれるので、教えるのが楽しいです。
さて、デジタル信号処理でもっとも有名なもののひとつがFFTです。
高速フーリエ変換(Fast Fourier Transform)は観測された信号に含まれる
周波数成分をスペクトルとして抽出するものです。
すべての波は複数のsin波で合成できるというフランスのフーリエの仮説に由来した
周波数分析技術です。
FFT解析ができる条件として、
・ 2^n 個のサンプルで構成されている信号であること。
・ 信号の開始点と終点が同じ値をとる周期関数であること。
の2つを満足していることです。
二つ目の条件を満足するために観測された生信号に窓関数を掛けることで
信号の前半部分と後半部分を徐々に減衰させ、1番目の信号値と最終の信号値を
ゼロにしてつなぐ、という処理をします。
信号のサンプリング周期も重要な要件であり、注目する信号成分に含まれている
であろう周波数の2倍よりやや早いサンプリング周波数で観測することにより
その周波数のスペクトルを得ることができます。
下の図の一番上のグラフは1kHzのサンプリング周波数で499.9Hzのsin波を
観測した結果です。
2番目は499.6941Hzのsin波を観測した結果です。
ともにサンプル数は2^15 (32768)サンプルです。
3番目、4番目のグラフは両者を拡大表示したものです。
団子やサングラスにみえるグラフは、このようなぎざぎざの連続になっています。
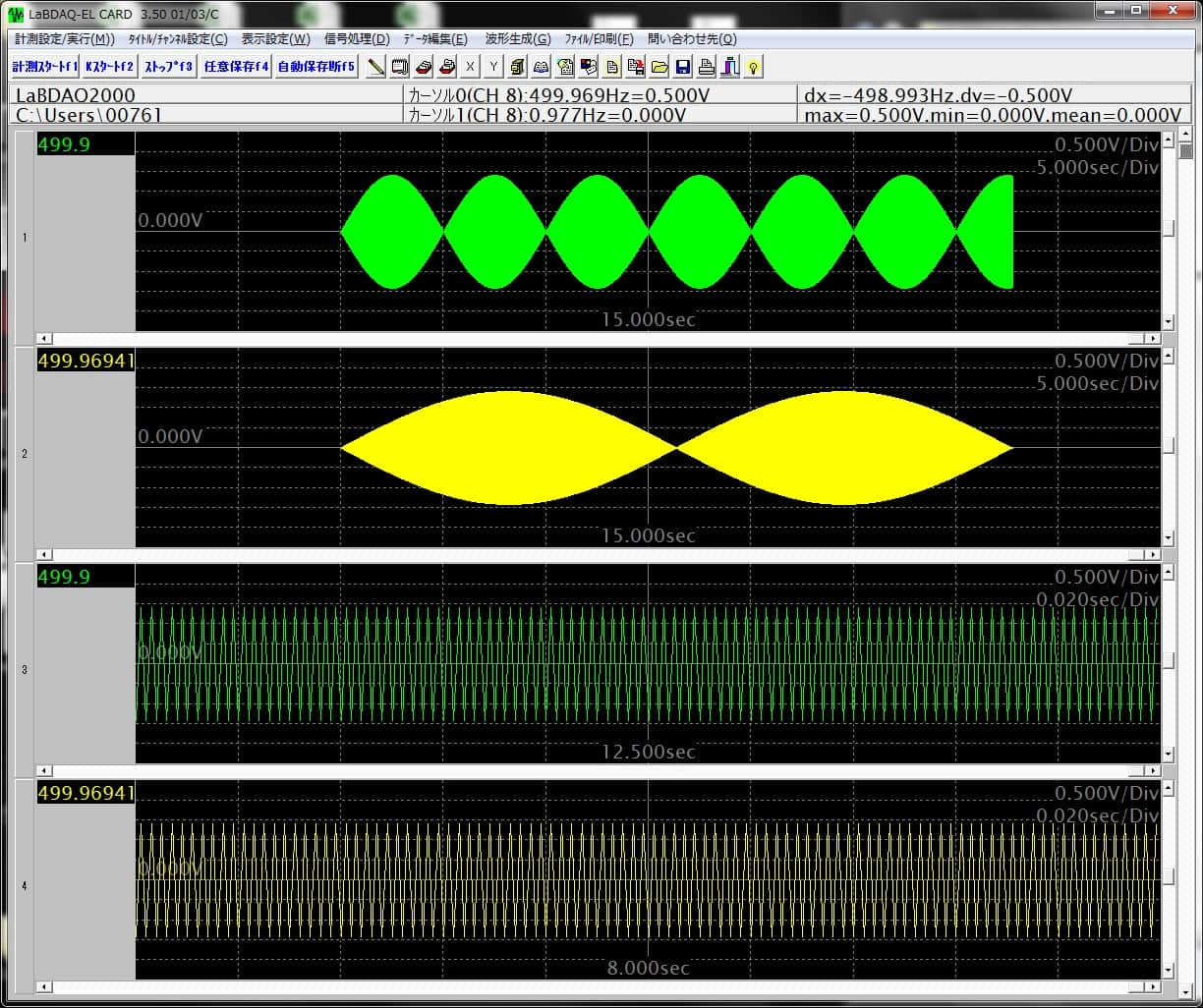
さて、両者をFFTするとどのような結果になるでしょうか?
そして、ナイキストサンプリングに関して、多くの技術者が大きな勘違いをしている
という現実・・・
それは、次回に・・・




















※コメント投稿者のブログIDはブログ作成者のみに通知されます