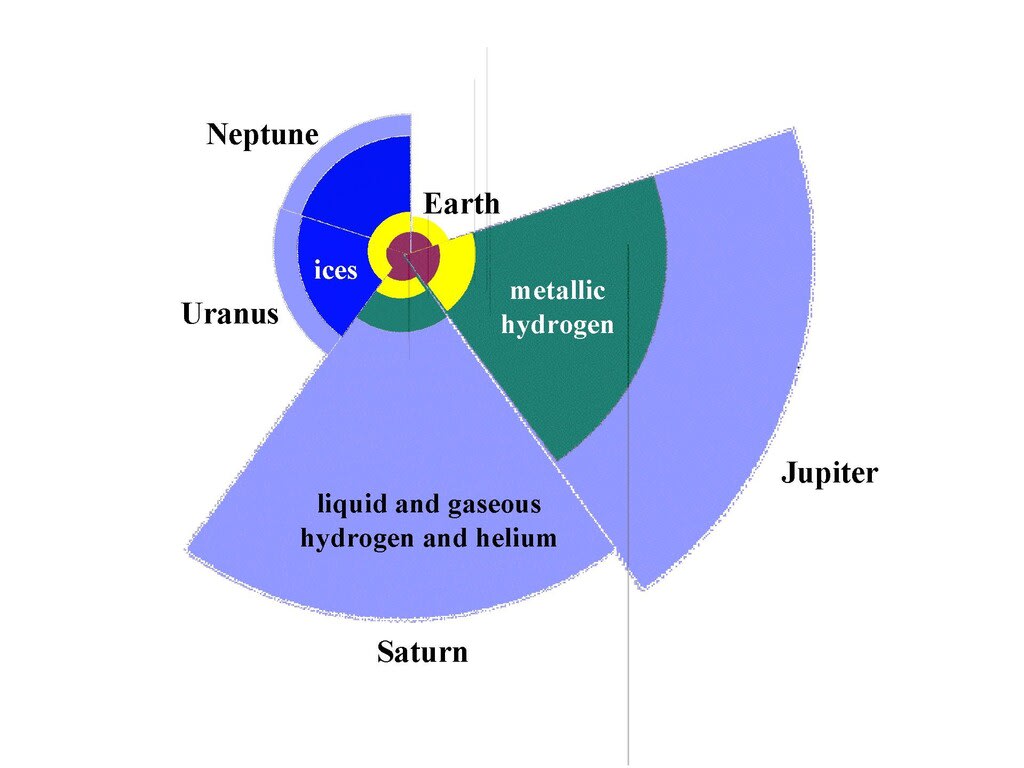
カッシーニによるリングの波の観測から土星内部に大きな重元素の核は無く水素とヘリウムの希薄な核が存在すると判断されている。以下、機械翻訳。
巨大惑星における希薄な核の長期存在に対する制約
要約
環地震学は最近、土星の内部に内部重力波が存在し、その内部重力波が中心から始まって土星の半径の 60% まで広がっていることを明らかにした。この内部は、今日土星の安定した層状の希薄な核として認識されている。同様に、木星の重力測定は、半径方向の範囲がまだ十分に制限されていない希薄な核の存在を示唆しています。これらの核は二重拡散状態にある可能性が高く、長期的な安定性に疑問が生じます。実際、三重周期領域におけるこれまでの DNS (直接数値シミュレーション) 研究では、一部の領域では二重拡散対流が自発的に浅い対流層を形成する傾向があり、その領域が完全に対流になるまで層が粗くなることが示されています。この手紙では、温度と組成フラックスがドメイン境界で固定されるさまざまな境界条件を使用して、二重拡散対流における層状化の条件を研究します。流体の微視的拡散率と初期層別の強度を変化させて一連の DNS を実行します。以前に発見された現象の結果として、対流層が依然として形成されていることがわかりました。
𝛾
- 局所的な成層が流体の拡散率のみに依存する臨界閾値を下回ると必ず発生する不安定性。また、層が形成されると成長し、最終的にはドメイン全体を占めることもわかります。したがって、私たちの研究は、新しい境界条件にもかかわらず、以前の研究の結果を回復し、この動作が普遍的であることを示唆しています。したがって、今日、土星の安定した層状の核の存在は、この閾値に到達したことがないことを示唆しており、このことが土星の形成と進化のシナリオに新たな制約を課している。
流体力学 - 不安定性 - 惑星と衛星: ガス惑星 - 惑星と衛星: 内部 - 乱流
巨大惑星における希薄な核の長期存在に対する制約
要約
環地震学は最近、土星の内部に内部重力波が存在し、その内部重力波が中心から始まって土星の半径の 60% まで広がっていることを明らかにした。この内部は、今日土星の安定した層状の希薄な核として認識されている。同様に、木星の重力測定は、半径方向の範囲がまだ十分に制限されていない希薄な核の存在を示唆しています。これらの核は二重拡散状態にある可能性が高く、長期的な安定性に疑問が生じます。実際、三重周期領域におけるこれまでの DNS (直接数値シミュレーション) 研究では、一部の領域では二重拡散対流が自発的に浅い対流層を形成する傾向があり、その領域が完全に対流になるまで層が粗くなることが示されています。この手紙では、温度と組成フラックスがドメイン境界で固定されるさまざまな境界条件を使用して、二重拡散対流における層状化の条件を研究します。流体の微視的拡散率と初期層別の強度を変化させて一連の DNS を実行します。以前に発見された現象の結果として、対流層が依然として形成されていることがわかりました。
𝛾
- 局所的な成層が流体の拡散率のみに依存する臨界閾値を下回ると必ず発生する不安定性。また、層が形成されると成長し、最終的にはドメイン全体を占めることもわかります。したがって、私たちの研究は、新しい境界条件にもかかわらず、以前の研究の結果を回復し、この動作が普遍的であることを示唆しています。したがって、今日、土星の安定した層状の核の存在は、この閾値に到達したことがないことを示唆しており、このことが土星の形成と進化のシナリオに新たな制約を課している。
流体力学 - 不安定性 - 惑星と衛星: ガス惑星 - 惑星と衛星: 内部 - 乱流
1導入
「コア降着」メカニズムによる単純な形成シナリオは、巨大ガス惑星内部の伝統的な見解として知られている、木星と土星の中心近くに集中した重元素のコンパクトな塊の存在を予測します(サフロノフ、1969年;ペリーとキャメロン、1974年;水野ら、1978年;水野さん1980年;ポラックら、1996年;ギヨット、2005年)。過去数年にわたって、ジュノーミッションからの木星の重力場に関する新しい高精度の制約が得られました(Bolton et al.,2017年;フォークナーら、2017年;デュランテら、2020年)、およびカッシーニ ミッションからの土星の重力場と地震振動周波数(Hedman & Nicholson、2013年、2014年;ヘドマンら、2018年;フレンチら、2019年;イスら、2019年)、これらの惑星の内部構造についての私たちの理解に革命をもたらし、この伝統的な見方に疑問を投げかける観察証拠を提供しました。豊富な証拠は、これらの惑星には、少なくとも 100 メートルまで広がる希薄な、またはあいまいな核があることを示唆しています。
~50% 土星の場合の惑星の半径(フラー、2014年;マンコビッチ&フラー、2021年)、木星の場合は半径の最大 30% ~ 70% (Wahl et al.,2017年;ドブラス&シャブリエ、2019年;ミゲルら、2022年;イディニとスティーブンソン、2022年;ミリッツァーら、2022年;ハワードら、2023年)。これらの核は重元素と H/He 流体の混合物で構成されており、豊富な重元素は惑星の中心に向かって増加するため、強力に安定化する組成勾配が形成されます。
土星の内部は重力場だけでなく環地震学によっても制約されているため、土星の場合は特に説得力があります(マーリーとポルコ、1993年;フラー、2014年;マンコビッチ2020年;マンコビッチ&フラー、2021年)。マンコビッチ&フラー(2021年) は 最近、安定に成層された希薄なコア構造の強力な証拠を発見しました。これは、内部重力波法線モードを許容し、自由対流していないことを意味します。同様の地震的制約は木星では利用できませんが、代わりにジュノーのミッションのおかげで重力場のより正確な測定が可能になりました。 H/He 混合物のいくつかの異なる高圧状態方程式を使用するさまざまなグループによって、この重力場に適合するこれまでに公開されたすべての内部モデルは、希薄な炉心を必要とします(Miguel et al.,2022年;イディニとスティーブンソン、2022年;ミリッツァーら、2022年;ハワードら、2023年)。しかし、木星の核の本当の範囲と、それが今日静的に安定しているかどうかは、H-He の状態方程式に関する私たちの知識には比較的大きな不確実性があり、それが木星の重力場の解釈をどのように複雑にするかにより不明のままです(Howard etみんな、2023年)。
重力場やリング地震学から惑星の内部構造を再構築することを目的とした内部モデルは、本質的に静的なモデルです。さらに、そのようなモデルには通常、惑星内部の熱構造を制約する力がほとんどありません。ただし、乱流運動に対する流体の安定性と、これらの運動によって引き起こされる混合が重元素の分布に及ぼす影響を考慮することによって、追加の情報と制約を得ることができます。たとえば、静的モデルでは、希薄なコアが強い組成勾配をサポートできる可能性がありますが、温度勾配の強さに応じて、その解決策は流体力学の観点からは非物理的になる可能性があります。実際、後者が安定化する組成勾配にもかかわらず何らかの形の対流を引き起こすのに十分強い場合、乱流の動きが炉心全体の重元素を急速に均質化する可能性がある。したがって、この点において、転倒対流または二重拡散対流による対流混合に対する希薄コアの安定性を確立することが重要です。
したがって、以下では、不安定化する温度勾配を有するが、強力に安定化する重元素勾配を有する土星のような希薄な核の特性を研究します(したがって、核全体はルドゥ基準で安定します)。それでも、このタイプの成層は、場合によっては振動二重拡散対流 (以下、ODDC) に対して不安定になる可能性があり、層化による二次的な対流不安定性も発生します (これについては下記を参照)。 ODDC は半対流とも呼ばれ、拡散的に不安定化した重力波によって引き起こされる弱い対流の一種です(Walin、1964年;加藤さん1966年;ベインズ&ギル、1969年)。これは主に 3 つの無次元パラメータによって支配されます: プラントル数𝑃𝑟、拡散率𝜏、および逆密度比𝑅^−1 (ローゼンブラムら、2011年)、それぞれ次のように定義されます。
𝑃𝑟 = 𝜈/𝜅𝑇、𝜏=𝜅𝐶/𝜅𝑇、𝑅^−1 = |𝑁𝐶^2/𝑁𝑇^2|、 (1)
どこ𝜈流体の動粘度です。
𝜅𝐶そして𝜅𝑇はそれぞれ組成拡散率と熱拡散率、
𝑁𝑇2そして𝑁𝐶2は、それぞれ熱成層と組成成層によるブルント・ヴァイサラ周波数です。プラントル数と拡散率は流体の特性を特徴付けるものですが、逆密度比は、𝑅^−1、層化の強度を定義し、より強く層化された領域ほど、より大きな領域を持ちます。
𝑅^−1。 ODDC に対する線形不安定性の基準は(Walin,1964年;加藤さん1966年) :
1 ≤ 𝑅^−1 ≤ (𝑃𝑟+1)/(𝑃𝑟+𝜏) ≡ 𝑅𝐶^−1。 (2)
限界𝑅^−1 = 1は Ledoux 基準に対応し、流体の領域は次のようになります。𝑅^-1 ≤ 1 転倒対流に対して不安定です。ある地域
𝑅^−1 ≥ 𝑅𝐶^−1 一方、ODDC に対して線形安定です。

図 1. 左: 無次元平均垂直密度プロファイルの時系列 (横軸に āρ、z 座標をとったもの)
縦軸)P r = τ = 0.1およびR0^−1 = 4.0。の場合 各線は特定の時間における平均密度プロファイルを表し、それぞれの
密度プロファイルは、視覚化を容易にするために、以前のタイム ステップから水平方向にオフセット (シフト) されています。 ラインは 2500 回ごとにプロットされます
単位は 10 種類の色で増分されます。 各青い線は、Δt = 25,000 時間単位の増分に対応します。 右: 逆密度
比率(縦軸)対時間(横軸):R^−1(0、t) (緑)、および R^−1(±75, t) (オレンジ色)。 赤い水平破線
RL^−1≃ 1.5、を示します これは P r = τ = 0.1 の階層化閾値です。

図 2. 図 1 と同様、P r = τ = 0.1 および R0^−1 = 2.5。 の場合
左: 垂直密度プロファイルの時系列。 それぞれの青いラインΔt = 12,500 時間単位増分に相当します。 右: 逆密度比 vs 時間: R^−1(0、t)(緑)、R^−1(±75、t)(オレンジ)。 赤い横破線はRL^−1 ≃ 1.5、を示します
これは P r = τ = 0.1 の階層化閾値であり、黒
破線は、対流が発生したときの t = 60,000 に対応します。

図 3. 図 1 と同様、P r = τ = 0.1 および R0^−1 = 1.75。の場合 左: 垂直密度プロファイルの時系列。 それぞれの青いライン
Δt = 2000 時間単位増分に相当します。 さまざまな進化段階は矢印でマークされています。 右: 逆向き密度比 vs 時間: R^−1
(0、t)(緑)、R^−1(±75, t) (オレンジ色)。 赤い横破線はRL^−1 ≃ 1.5、を示します
つまりP r = τ = 0.1 の層化閾値、黒い破線は対流が引き起こされたときの t = 2000 に対応します。

図 4. 図 1 と同様、P r = τ = 0.1 および R0^−1 = 1.25。の場合
左: 垂直密度プロファイルの時系列。 それぞれの青いライン
Δt = 1,000 時間単位増分に相当します。 さまざまな進化段階は矢印でマークされています。 右: 逆向き
密度比 vs 時間: R^−1(0、t)(緑)、R^−1(±75, t) (オレンジ色)。 赤い横破線はRL^−1 ≃ 1.5、を示します
つまりP r = τ = 0.1 の階層化閾値。
4. 議論と結論
で行われる DNS の理想的な性質を考慮すると、
前のセクションでは、一般性に疑問を抱く人もいるかもしれません
この結論の。 ただし、非常に堅牢であると考えられます。 まず、次の結果を提示しましたが、
P r = τ = 0.1、他の場合でも非常に似た結果が得られます。
入力パラメータは、私たちが観察した限りでは、
P r = τ = 0.3 で考えられるケースの同じシーケンス。
RL^−1 の役割に関しても同じ結論(表1を参照)。 第二に、Radko (2007) は、密度階段 (
薄い安定した界面)は、密度束が層の高さとともに増加するか、または
界面の成層化とともに減少する場合。 これらの条件は両方とも、形成された ODDC 階段で満たされます。
γ 不安定性による (Wood et al. 2013; Moll et al. 2017)、
図4 (より一般的には弱成層領域)で観察された粗大化プロセスを示唆しています
普遍的であり、地域全体が完全に完了するまで停止しません
対流性。 図2 と 3で示すケースの堅牢性 では、対流層が侵食されて成長します。
近くの ODDC 層は、やや明確ではありませんが、エントレインメント プロセスが発生するため、可能性は依然として残っています。
動的なタイムスケールでの再階層化ODDC レイヤー (保存するために必要) が発生します
はるかに長い進化のタイムスケールで。 ついに巨人
私たちの太陽系の惑星は高速回転しているので、
回転がγ不安定性にどのような影響を与えるのか疑問に思う人もいるかもしれない
そして対流層の進化。 モール&ガロード(2017) は、γ 不安定性は回転によって直接影響を受けないが、磁束比 γ^−1 は影響を受けることを示しました。
それ自体、そしてそのR^−1 への依存性、両方とも惑星に依存する可能性があります
回転率。 したがって、私たちの一般的な結論はローテーションが存在する場合でも引き続き維持されますが、重要な点は次のとおりです。
層形成の逆密度比 RL^−1
高速で回転する惑星の回転速度の関数である可能性があります。 回転が機体に与える影響を徹底的に研究。
磁束比γ^−1したがって、 が必要です。 さらに、フエンテス
他。 (2023) は、回転によって対流領域に隣接する安定成層領域の浸食速度が遅くなる可能性があることを示しました。 これにより速度が低下する可能性はありますが、完全に遅くすることはできません
完全対流ゾーンの成長が停止すると、
が作成されました。
もちろん、この論文で研究したモデル系の詳細な進化を惑星の拡散核の進化と直接比較すべきではありません。
私たちが使用した境界条件は固定と
両方の境界上の熱流束と組成が等しい、
しかし、実際にはそうではありません。 で
特に、これらの境界がどこにあると仮定するかによって、上部と下部のフラックスは異なる可能性があります。
地球上で時間の経過とともに相互に進化し、
進化のタイムスケール (Hindman & Fuentes 2023)。 しかし、我々は、
γ 不安定性は局所的なプロセスであり、
境界で何が起こるか、そしてそれにのみ依存します
任意の時点におけるそのコアの局所的な層別。
このため、次の結論が成り立ちます。
1. Woodらの結果を確認します。 (2013) とミルーら (2012) γ 不安定性が関与している
超断熱温度勾配を持つ安定成層領域のダイナミクスにおける基本的な役割。 より具体的には、次のことがわかりました。
局所的な逆密度比 R^−1 が大きくなると同時に、γ 不安定性が局所的に対流層の形成を引き起こすこと
(z, t) (式 27 を参照)、RL^−1 を下回る
(P r, τ ) (式 4 を参照)。 のある地域のみ
R^−1(z, t) > RL^−1、 ∀z、 t は長期的に残留することができます。
ODDC の状態。 ちなみに、これは P r と P r の両方について適切な推定値を持つことが重要であることを示しています。
τ (French et al. 2019; Preising et al. 2023 を参照)
RL^−1(P r, τ ) (ミルー他。 2012) の良いモデルとしても
。 惑星が急速に回転している場合、RL^−1
回転数にもよるかもしれません。
2. Radko (2007) の結果と組み合わせた我々の結果、
巨大惑星の組成的に成層された領域を長命でよく混合された層として描く標準的なパラダイムに挑戦します。
薄い拡散界面によって分離された浅い対流層 (Stevenson 1982)。 これはそうではありません
私たちのシミュレーションの結果として見られました。 で
中等度の層別化では自発的に
対流層が形成され、常に成長しているように見えます。
対流ゾーンがドメイン全体を占めるまでマージします。 これらのプロセスは急速に発生し、
不可逆的に。 急速な回転は減速する可能性がありますが、プロセスを完全に妨げることはできないと考えています。
3. 土星が観測されている事実
拡張された安定した層状コアは、次のことを示唆しています。
R^−1(z, t) がしきい値 RL^−1 を下回ることはありません
の進化を通じてそのコアで
惑星。 これは形成を抑制するのに役立つ可能性があります
そして土星の進化モデル。
惑星に関してはさらに多くの調査が行われています
これらの結果を踏まえて検討すべきモデリング。
私たちは、今日の土星の希薄な核が安定して層状化しているという強力な証拠を持っています (Fuller 2014; Mankovich & Fuller)
2021年; フォートニーら。 2023年)。 ここでの私たちの研究は次のことを示唆しています
この安定した層状構造は、土星が惑星の形成中にすでに確立されていたに違いありません。 これ
中心温度(そして
希薄なコア内の対応する温度勾配)
その時だけでなく、結成までの間はいつでも
今日まで、γ 不安定性が決して引き起こされないことを保証します。 これらの温度制約は、次のことを直接的に伝えます。
今日の静的構造モデルと、測定された惑星の再現を目的とした熱進化モデル
現在の年齢での明るさ。
木星に対する地震的制約がなければ、私たちは次のようにすることはできません。
希薄なコアの範囲と熱状態を簡単に制限できます。 土星と同じように、木星も
希薄なコアも安定して成層されます。 このシナリオは、
内部重力波という示唆によって裏付けられています
このようなコアに閉じ込められると、十分な重力が発生します。
衛星イオによって引き起こされる潮汐の重力場を乱す兆候 (Idini & Stevenson 2022)。 あるいは、
おそらく初期熱エネルギーが高いほど、
巨大な木星とそれに対応するより高い初期中心
気温が地球を異なる状態に陥らせ、
過去に時々対流を引き起こしたことがありましたので、
現在の希薄コアは完全または部分的に均質化されています。
条件を解釈するにはさらなる分析が必要です
予想される条件に対するここでの不安定性
木星と土星の内部。 巨大な惑星では、そのような作業では自明ではない計算を考慮する必要があります。
材料特性が深さとともにどのように変化するかについて説明します。
H-He 流体と重元素の混合物の断熱または超断熱挙動とその中の不確実性。 今後の研究では、新たな発見を目指します。
中心温度の範囲、強度の制限
組成勾配と希薄物の半径方向の広がり
木星と土星の核を調査し、現在何が存在するのかを評価します。
ここで開発された混合議論を考慮すると、過去の内部構造が可能です。
で。 そしてPG。 ~からの援助に感謝の意を表します
「Dedalus」開発チームとNationalからのサポート
科学財団助成金 AST-1908338。 B.I. は、カリフォルニア大学学長の博士研究員プログラムによって支援されています。 シミュレーションは、Extreme Science and Engineering Discovery Environment (XSEDE) Expanse スーパーコンピューターを使用して実行されました。
サンディエゴ スーパーコンピュータ センターでは、TG-PHY210050 の割り当てにより、Lux スーパーコンピュータと同様に
カリフォルニア大学サンタクルーズ校で、NSF MRI 助成金 AST1828315 の資金提供を受けています。
「コア降着」メカニズムによる単純な形成シナリオは、巨大ガス惑星内部の伝統的な見解として知られている、木星と土星の中心近くに集中した重元素のコンパクトな塊の存在を予測します(サフロノフ、1969年;ペリーとキャメロン、1974年;水野ら、1978年;水野さん1980年;ポラックら、1996年;ギヨット、2005年)。過去数年にわたって、ジュノーミッションからの木星の重力場に関する新しい高精度の制約が得られました(Bolton et al.,2017年;フォークナーら、2017年;デュランテら、2020年)、およびカッシーニ ミッションからの土星の重力場と地震振動周波数(Hedman & Nicholson、2013年、2014年;ヘドマンら、2018年;フレンチら、2019年;イスら、2019年)、これらの惑星の内部構造についての私たちの理解に革命をもたらし、この伝統的な見方に疑問を投げかける観察証拠を提供しました。豊富な証拠は、これらの惑星には、少なくとも 100 メートルまで広がる希薄な、またはあいまいな核があることを示唆しています。
~50% 土星の場合の惑星の半径(フラー、2014年;マンコビッチ&フラー、2021年)、木星の場合は半径の最大 30% ~ 70% (Wahl et al.,2017年;ドブラス&シャブリエ、2019年;ミゲルら、2022年;イディニとスティーブンソン、2022年;ミリッツァーら、2022年;ハワードら、2023年)。これらの核は重元素と H/He 流体の混合物で構成されており、豊富な重元素は惑星の中心に向かって増加するため、強力に安定化する組成勾配が形成されます。
土星の内部は重力場だけでなく環地震学によっても制約されているため、土星の場合は特に説得力があります(マーリーとポルコ、1993年;フラー、2014年;マンコビッチ2020年;マンコビッチ&フラー、2021年)。マンコビッチ&フラー(2021年) は 最近、安定に成層された希薄なコア構造の強力な証拠を発見しました。これは、内部重力波法線モードを許容し、自由対流していないことを意味します。同様の地震的制約は木星では利用できませんが、代わりにジュノーのミッションのおかげで重力場のより正確な測定が可能になりました。 H/He 混合物のいくつかの異なる高圧状態方程式を使用するさまざまなグループによって、この重力場に適合するこれまでに公開されたすべての内部モデルは、希薄な炉心を必要とします(Miguel et al.,2022年;イディニとスティーブンソン、2022年;ミリッツァーら、2022年;ハワードら、2023年)。しかし、木星の核の本当の範囲と、それが今日静的に安定しているかどうかは、H-He の状態方程式に関する私たちの知識には比較的大きな不確実性があり、それが木星の重力場の解釈をどのように複雑にするかにより不明のままです(Howard etみんな、2023年)。
重力場やリング地震学から惑星の内部構造を再構築することを目的とした内部モデルは、本質的に静的なモデルです。さらに、そのようなモデルには通常、惑星内部の熱構造を制約する力がほとんどありません。ただし、乱流運動に対する流体の安定性と、これらの運動によって引き起こされる混合が重元素の分布に及ぼす影響を考慮することによって、追加の情報と制約を得ることができます。たとえば、静的モデルでは、希薄なコアが強い組成勾配をサポートできる可能性がありますが、温度勾配の強さに応じて、その解決策は流体力学の観点からは非物理的になる可能性があります。実際、後者が安定化する組成勾配にもかかわらず何らかの形の対流を引き起こすのに十分強い場合、乱流の動きが炉心全体の重元素を急速に均質化する可能性がある。したがって、この点において、転倒対流または二重拡散対流による対流混合に対する希薄コアの安定性を確立することが重要です。
したがって、以下では、不安定化する温度勾配を有するが、強力に安定化する重元素勾配を有する土星のような希薄な核の特性を研究します(したがって、核全体はルドゥ基準で安定します)。それでも、このタイプの成層は、場合によっては振動二重拡散対流 (以下、ODDC) に対して不安定になる可能性があり、層化による二次的な対流不安定性も発生します (これについては下記を参照)。 ODDC は半対流とも呼ばれ、拡散的に不安定化した重力波によって引き起こされる弱い対流の一種です(Walin、1964年;加藤さん1966年;ベインズ&ギル、1969年)。これは主に 3 つの無次元パラメータによって支配されます: プラントル数𝑃𝑟、拡散率𝜏、および逆密度比𝑅^−1 (ローゼンブラムら、2011年)、それぞれ次のように定義されます。
𝑃𝑟 = 𝜈/𝜅𝑇、𝜏=𝜅𝐶/𝜅𝑇、𝑅^−1 = |𝑁𝐶^2/𝑁𝑇^2|、 (1)
どこ𝜈流体の動粘度です。
𝜅𝐶そして𝜅𝑇はそれぞれ組成拡散率と熱拡散率、
𝑁𝑇2そして𝑁𝐶2は、それぞれ熱成層と組成成層によるブルント・ヴァイサラ周波数です。プラントル数と拡散率は流体の特性を特徴付けるものですが、逆密度比は、𝑅^−1、層化の強度を定義し、より強く層化された領域ほど、より大きな領域を持ちます。
𝑅^−1。 ODDC に対する線形不安定性の基準は(Walin,1964年;加藤さん1966年) :
1 ≤ 𝑅^−1 ≤ (𝑃𝑟+1)/(𝑃𝑟+𝜏) ≡ 𝑅𝐶^−1。 (2)
限界𝑅^−1 = 1は Ledoux 基準に対応し、流体の領域は次のようになります。𝑅^-1 ≤ 1 転倒対流に対して不安定です。ある地域
𝑅^−1 ≥ 𝑅𝐶^−1 一方、ODDC に対して線形安定です。

図 1. 左: 無次元平均垂直密度プロファイルの時系列 (横軸に āρ、z 座標をとったもの)
縦軸)P r = τ = 0.1およびR0^−1 = 4.0。の場合 各線は特定の時間における平均密度プロファイルを表し、それぞれの
密度プロファイルは、視覚化を容易にするために、以前のタイム ステップから水平方向にオフセット (シフト) されています。 ラインは 2500 回ごとにプロットされます
単位は 10 種類の色で増分されます。 各青い線は、Δt = 25,000 時間単位の増分に対応します。 右: 逆密度
比率(縦軸)対時間(横軸):R^−1(0、t) (緑)、および R^−1(±75, t) (オレンジ色)。 赤い水平破線
RL^−1≃ 1.5、を示します これは P r = τ = 0.1 の階層化閾値です。

図 2. 図 1 と同様、P r = τ = 0.1 および R0^−1 = 2.5。 の場合
左: 垂直密度プロファイルの時系列。 それぞれの青いラインΔt = 12,500 時間単位増分に相当します。 右: 逆密度比 vs 時間: R^−1(0、t)(緑)、R^−1(±75、t)(オレンジ)。 赤い横破線はRL^−1 ≃ 1.5、を示します
これは P r = τ = 0.1 の階層化閾値であり、黒
破線は、対流が発生したときの t = 60,000 に対応します。

図 3. 図 1 と同様、P r = τ = 0.1 および R0^−1 = 1.75。の場合 左: 垂直密度プロファイルの時系列。 それぞれの青いライン
Δt = 2000 時間単位増分に相当します。 さまざまな進化段階は矢印でマークされています。 右: 逆向き密度比 vs 時間: R^−1
(0、t)(緑)、R^−1(±75, t) (オレンジ色)。 赤い横破線はRL^−1 ≃ 1.5、を示します
つまりP r = τ = 0.1 の層化閾値、黒い破線は対流が引き起こされたときの t = 2000 に対応します。

図 4. 図 1 と同様、P r = τ = 0.1 および R0^−1 = 1.25。の場合
左: 垂直密度プロファイルの時系列。 それぞれの青いライン
Δt = 1,000 時間単位増分に相当します。 さまざまな進化段階は矢印でマークされています。 右: 逆向き
密度比 vs 時間: R^−1(0、t)(緑)、R^−1(±75, t) (オレンジ色)。 赤い横破線はRL^−1 ≃ 1.5、を示します
つまりP r = τ = 0.1 の階層化閾値。
4. 議論と結論
で行われる DNS の理想的な性質を考慮すると、
前のセクションでは、一般性に疑問を抱く人もいるかもしれません
この結論の。 ただし、非常に堅牢であると考えられます。 まず、次の結果を提示しましたが、
P r = τ = 0.1、他の場合でも非常に似た結果が得られます。
入力パラメータは、私たちが観察した限りでは、
P r = τ = 0.3 で考えられるケースの同じシーケンス。
RL^−1 の役割に関しても同じ結論(表1を参照)。 第二に、Radko (2007) は、密度階段 (
薄い安定した界面)は、密度束が層の高さとともに増加するか、または
界面の成層化とともに減少する場合。 これらの条件は両方とも、形成された ODDC 階段で満たされます。
γ 不安定性による (Wood et al. 2013; Moll et al. 2017)、
図4 (より一般的には弱成層領域)で観察された粗大化プロセスを示唆しています
普遍的であり、地域全体が完全に完了するまで停止しません
対流性。 図2 と 3で示すケースの堅牢性 では、対流層が侵食されて成長します。
近くの ODDC 層は、やや明確ではありませんが、エントレインメント プロセスが発生するため、可能性は依然として残っています。
動的なタイムスケールでの再階層化ODDC レイヤー (保存するために必要) が発生します
はるかに長い進化のタイムスケールで。 ついに巨人
私たちの太陽系の惑星は高速回転しているので、
回転がγ不安定性にどのような影響を与えるのか疑問に思う人もいるかもしれない
そして対流層の進化。 モール&ガロード(2017) は、γ 不安定性は回転によって直接影響を受けないが、磁束比 γ^−1 は影響を受けることを示しました。
それ自体、そしてそのR^−1 への依存性、両方とも惑星に依存する可能性があります
回転率。 したがって、私たちの一般的な結論はローテーションが存在する場合でも引き続き維持されますが、重要な点は次のとおりです。
層形成の逆密度比 RL^−1
高速で回転する惑星の回転速度の関数である可能性があります。 回転が機体に与える影響を徹底的に研究。
磁束比γ^−1したがって、 が必要です。 さらに、フエンテス
他。 (2023) は、回転によって対流領域に隣接する安定成層領域の浸食速度が遅くなる可能性があることを示しました。 これにより速度が低下する可能性はありますが、完全に遅くすることはできません
完全対流ゾーンの成長が停止すると、
が作成されました。
もちろん、この論文で研究したモデル系の詳細な進化を惑星の拡散核の進化と直接比較すべきではありません。
私たちが使用した境界条件は固定と
両方の境界上の熱流束と組成が等しい、
しかし、実際にはそうではありません。 で
特に、これらの境界がどこにあると仮定するかによって、上部と下部のフラックスは異なる可能性があります。
地球上で時間の経過とともに相互に進化し、
進化のタイムスケール (Hindman & Fuentes 2023)。 しかし、我々は、
γ 不安定性は局所的なプロセスであり、
境界で何が起こるか、そしてそれにのみ依存します
任意の時点におけるそのコアの局所的な層別。
このため、次の結論が成り立ちます。
1. Woodらの結果を確認します。 (2013) とミルーら (2012) γ 不安定性が関与している
超断熱温度勾配を持つ安定成層領域のダイナミクスにおける基本的な役割。 より具体的には、次のことがわかりました。
局所的な逆密度比 R^−1 が大きくなると同時に、γ 不安定性が局所的に対流層の形成を引き起こすこと
(z, t) (式 27 を参照)、RL^−1 を下回る
(P r, τ ) (式 4 を参照)。 のある地域のみ
R^−1(z, t) > RL^−1、 ∀z、 t は長期的に残留することができます。
ODDC の状態。 ちなみに、これは P r と P r の両方について適切な推定値を持つことが重要であることを示しています。
τ (French et al. 2019; Preising et al. 2023 を参照)
RL^−1(P r, τ ) (ミルー他。 2012) の良いモデルとしても
。 惑星が急速に回転している場合、RL^−1
回転数にもよるかもしれません。
2. Radko (2007) の結果と組み合わせた我々の結果、
巨大惑星の組成的に成層された領域を長命でよく混合された層として描く標準的なパラダイムに挑戦します。
薄い拡散界面によって分離された浅い対流層 (Stevenson 1982)。 これはそうではありません
私たちのシミュレーションの結果として見られました。 で
中等度の層別化では自発的に
対流層が形成され、常に成長しているように見えます。
対流ゾーンがドメイン全体を占めるまでマージします。 これらのプロセスは急速に発生し、
不可逆的に。 急速な回転は減速する可能性がありますが、プロセスを完全に妨げることはできないと考えています。
3. 土星が観測されている事実
拡張された安定した層状コアは、次のことを示唆しています。
R^−1(z, t) がしきい値 RL^−1 を下回ることはありません
の進化を通じてそのコアで
惑星。 これは形成を抑制するのに役立つ可能性があります
そして土星の進化モデル。
惑星に関してはさらに多くの調査が行われています
これらの結果を踏まえて検討すべきモデリング。
私たちは、今日の土星の希薄な核が安定して層状化しているという強力な証拠を持っています (Fuller 2014; Mankovich & Fuller)
2021年; フォートニーら。 2023年)。 ここでの私たちの研究は次のことを示唆しています
この安定した層状構造は、土星が惑星の形成中にすでに確立されていたに違いありません。 これ
中心温度(そして
希薄なコア内の対応する温度勾配)
その時だけでなく、結成までの間はいつでも
今日まで、γ 不安定性が決して引き起こされないことを保証します。 これらの温度制約は、次のことを直接的に伝えます。
今日の静的構造モデルと、測定された惑星の再現を目的とした熱進化モデル
現在の年齢での明るさ。
木星に対する地震的制約がなければ、私たちは次のようにすることはできません。
希薄なコアの範囲と熱状態を簡単に制限できます。 土星と同じように、木星も
希薄なコアも安定して成層されます。 このシナリオは、
内部重力波という示唆によって裏付けられています
このようなコアに閉じ込められると、十分な重力が発生します。
衛星イオによって引き起こされる潮汐の重力場を乱す兆候 (Idini & Stevenson 2022)。 あるいは、
おそらく初期熱エネルギーが高いほど、
巨大な木星とそれに対応するより高い初期中心
気温が地球を異なる状態に陥らせ、
過去に時々対流を引き起こしたことがありましたので、
現在の希薄コアは完全または部分的に均質化されています。
条件を解釈するにはさらなる分析が必要です
予想される条件に対するここでの不安定性
木星と土星の内部。 巨大な惑星では、そのような作業では自明ではない計算を考慮する必要があります。
材料特性が深さとともにどのように変化するかについて説明します。
H-He 流体と重元素の混合物の断熱または超断熱挙動とその中の不確実性。 今後の研究では、新たな発見を目指します。
中心温度の範囲、強度の制限
組成勾配と希薄物の半径方向の広がり
木星と土星の核を調査し、現在何が存在するのかを評価します。
ここで開発された混合議論を考慮すると、過去の内部構造が可能です。
で。 そしてPG。 ~からの援助に感謝の意を表します
「Dedalus」開発チームとNationalからのサポート
科学財団助成金 AST-1908338。 B.I. は、カリフォルニア大学学長の博士研究員プログラムによって支援されています。 シミュレーションは、Extreme Science and Engineering Discovery Environment (XSEDE) Expanse スーパーコンピューターを使用して実行されました。
サンディエゴ スーパーコンピュータ センターでは、TG-PHY210050 の割り当てにより、Lux スーパーコンピュータと同様に
カリフォルニア大学サンタクルーズ校で、NSF MRI 助成金 AST1828315 の資金提供を受けています。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます