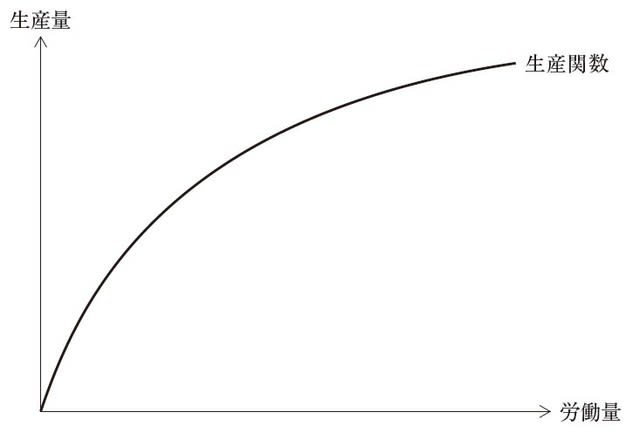
まず最初に、生産関数は投入量と生産量の関係を示すものです。
Y = f(X) ・・・ 生産量=f(投入量)
※生産者理論の最初に出てくる費用関数は生産量と費用の関係を示すものです。
C = f(Y) ・・・ 費用=f(生産量)
投入量は資本Kと労働Lの関数で表現されることが多いです。
Y=Kのα乗 × Lのβ乗
K,Lで偏微分したもの δY/δK、δY/δLはそれぞれ限界生産物と呼ばれます。
資本・労働ともに収穫逓減を想定すれば、α<1、β<1となります。
このとき、製品の価格をpとすれば、p・δY/δK、p・δY/δLはそれぞれ資本・労働の単位当たりの価格となります。
これをもとに等量曲線を描くと以下のようになります。
(消費者理論における 限界効用逓減⇒無差別曲線 の話と同じです)

また、規模に関しては以下のようになります。
α+β<1のとき 規模に関して収穫逓減
α+β=1のとき 規模に関して収穫一定
α+β>1のとき 規模に関して収穫逓増



















※コメント投稿者のブログIDはブログ作成者のみに通知されます