
木星のガリレオ衛星の公転周期は1:2:4:8になってるのかと思えばカリストだけ外れてる。平均運動共鳴で相互作用する事でイオの移行がカリストまで伝わる。以下、機械翻訳。
ガリレオ衛星の長期進化:カリストの共鳴への捕獲
(2020年1月4日に提出)
環境。木星-イオ カップルの強い潮汐力散逸は、ラプラス共鳴に関与するすべての衛星(イオ、エウロパ、およびガニメデ)に広がり、軌道の移動につながります。
ねらい 太陽系の寿命にわたってガリレオ衛星の挙動を特徴付け、ラプラス共鳴の安定性を定量化することを目指しています。潮汐力散逸により、現在の共鳴からの脱出または新しい共鳴への捕獲が可能になるため、共鳴へのカリストの捕獲を調査します。
メソッド。最近の半分析モデルの改良バージョンを使用して、数百の伝播を実行します。ガニメデが外側に移動すると、カリストとの2:1の共鳴に近づき、システムに一時的な混chaとした動きを引き起こします。このため、共鳴的な出会いの結果の統計的な絵を描きます。
結果。システムは、2つの異なる結果に落ち着くことができます。A)3つの2:1の2体共鳴のチェーン(イオ-エウロパ、エウロパ-ガニメデ、およびガニメデ-カリスト)、またはB)2:1の2体を含む共鳴チェーン共鳴イオ-エウロパに加えて、エウロパ、ガニメデ、カリストの間で最も頻繁に、少なくとも1つの純粋な4:2:1 3体共鳴。ケースA(シミュレーションの56 %)では、ラプラス共鳴が常に保持され、離心率は0.01未満の小さな値に制限されたままです。ケースB(シミュレーションの44%)では、ラプラス共振が一般的に中断され、ガニメデとカリストの離心率が最大で約0.1に増加し、この構成が不安定になり、システムが新しい共振に追い込まれます。
結論。私たちの結果から、カリストの共鳴への取り込みは非常に可能性が高いようです(シミュレーションの100 %)。イオと木星の間の散逸の最新の推定値を仮定すると、共振遭遇は約1.5 Gyrsで今から起こります。したがって、ラプラス共鳴の安定性は少なくとも約1.5 Gyrsまで保証されます。
図1.衛星の第1フェーズにおける半長軸の変動
進化。 ラプラス共鳴により、潮汐力散逸はイオ、エウロパ、ガニメデに分布しています。 ズームインに示すように
ビューでは、イオは最初は内向きに移行し、次にエウロパやガニメデ。 カリストには永年的な傾向はありません。

図2.衛星の第1段階での離心率の変化進化。 イオとエウロパの離心率は最初減少し、その後、a2 / a1はほぼ一定のままで、新しい値に安定します
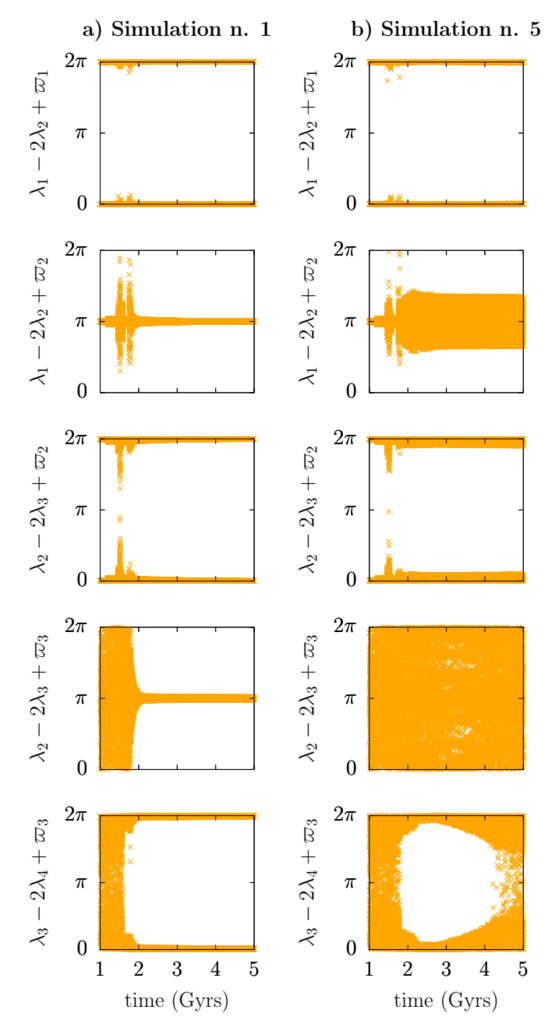
図3ケースAの1次共振角の典型的な進化
列a):λ2−2λ3+ $ 3が解放を開始します。 列b):λ2−2λ3+ $ 3循環し続けます。

図4.ケースBの1次共振角の典型的な進化
列a):λ2−2λ3+ $ 2が循環し始めます。 列b):λ2−2λ3+ $ 2解放し続けます。
5。結論
潮汐力散逸のため、ガリレオ衛星の軌道は時間とともにゆっくりと移行します。エネルギーは主に
イオと木星の間の潮汐力相互作用、しかしの影響その後、散逸は、衛星間で再分配されます
ラプラス共鳴。 10億年のタイムスケールで、これはイオ、エウロパ、ガニメデの外への移行。だから
現在、平均運動の共鳴に関与していない、カリストは非常に多く、これらのサイクルは何十億年も続くことがあります。各
新しい共鳴へのキャプチャは、新しい共鳴中心に向かって引き付けられる半長軸の小さなジャンプを生成します
線形ドリフトを再開する前に。
私たちの研究は、カリストとの共鳴的な出会いが明らかになりました
私たちが知っているように、ラプラス共鳴の特徴を破壊することができます
今日、イオとエウロパ間の2:1の共振(これは すべてのシミュレーションで持続します)。したがって、ラプラス共鳴
潮汐力散逸作用下では安定しているが、約1.5 Gyrsで発生するカリストとの共鳴的な出会い
今から。 4つの衛星すべてが常に最終的には
新しい共鳴チェーン、エウロパとガニメデがシミュレーションの37%で破壊されました。ラプラス
共鳴は、イオ、エウロパ、ガニメデの間の純粋な3体共鳴に変わります。ただし、これはまれな結果です
通常は数億年未満のシミュレーションの結果であり、です。この時間間隔の間に、エウロパの離心率が増加します。
衛星の軌道の傾きが再生されない
長期的なダイナミクスにおける役割:それらはまったく小さいままです
時と衛星のわずかな変化によってのみ影響を受けます
共鳴に入る、または共鳴から出る。このアプローチには、主に2つの制限があります。最初はハミルトニアンは、離心率の2次で切り捨てられます。
次のように、偏心が大きい場合、モデルの精度は低下します。
ケースBのいくつかのシミュレーション。これは最終結果に影響を与える可能性があります。
いくつかのシミュレーションのうち、分類スキームもこの結論で示されたパーセンテージ。さらに重要なのは、
高速角度でハミルトニアンを平均化するプロセス、多くの純粋な三体の組み合わせが削除され、特に
離心率の次数0の項。私たちが観察したのでシステムは、多数の弱い共振に閉じ込められる可能性があります。
平均化されていないモデルによって与えられる長期的な進化は、おそらくさらに共鳴的な捕獲を示し、
カリストはさらにありそうもない。ただし、追加の3体共鳴も、
ケースBを作成し、さらにシミュレーションをケースAに進めます。割合
したがって、私たちの研究で得られたものは指標とみなされるべきです。残念ながら、非平均を使用した5 Gyrsを超える統計研究
モデルでは、法外な計算時間が必要になります。
ガリレオ衛星の長期進化:カリストの共鳴への捕獲
(2020年1月4日に提出)
環境。木星-イオ カップルの強い潮汐力散逸は、ラプラス共鳴に関与するすべての衛星(イオ、エウロパ、およびガニメデ)に広がり、軌道の移動につながります。
ねらい 太陽系の寿命にわたってガリレオ衛星の挙動を特徴付け、ラプラス共鳴の安定性を定量化することを目指しています。潮汐力散逸により、現在の共鳴からの脱出または新しい共鳴への捕獲が可能になるため、共鳴へのカリストの捕獲を調査します。
メソッド。最近の半分析モデルの改良バージョンを使用して、数百の伝播を実行します。ガニメデが外側に移動すると、カリストとの2:1の共鳴に近づき、システムに一時的な混chaとした動きを引き起こします。このため、共鳴的な出会いの結果の統計的な絵を描きます。
結果。システムは、2つの異なる結果に落ち着くことができます。A)3つの2:1の2体共鳴のチェーン(イオ-エウロパ、エウロパ-ガニメデ、およびガニメデ-カリスト)、またはB)2:1の2体を含む共鳴チェーン共鳴イオ-エウロパに加えて、エウロパ、ガニメデ、カリストの間で最も頻繁に、少なくとも1つの純粋な4:2:1 3体共鳴。ケースA(シミュレーションの56 %)では、ラプラス共鳴が常に保持され、離心率は0.01未満の小さな値に制限されたままです。ケースB(シミュレーションの44%)では、ラプラス共振が一般的に中断され、ガニメデとカリストの離心率が最大で約0.1に増加し、この構成が不安定になり、システムが新しい共振に追い込まれます。
結論。私たちの結果から、カリストの共鳴への取り込みは非常に可能性が高いようです(シミュレーションの100 %)。イオと木星の間の散逸の最新の推定値を仮定すると、共振遭遇は約1.5 Gyrsで今から起こります。したがって、ラプラス共鳴の安定性は少なくとも約1.5 Gyrsまで保証されます。
図1.衛星の第1フェーズにおける半長軸の変動
進化。 ラプラス共鳴により、潮汐力散逸はイオ、エウロパ、ガニメデに分布しています。 ズームインに示すように
ビューでは、イオは最初は内向きに移行し、次にエウロパやガニメデ。 カリストには永年的な傾向はありません。

図2.衛星の第1段階での離心率の変化進化。 イオとエウロパの離心率は最初減少し、その後、a2 / a1はほぼ一定のままで、新しい値に安定します

図3ケースAの1次共振角の典型的な進化
列a):λ2−2λ3+ $ 3が解放を開始します。 列b):λ2−2λ3+ $ 3循環し続けます。

図4.ケースBの1次共振角の典型的な進化
列a):λ2−2λ3+ $ 2が循環し始めます。 列b):λ2−2λ3+ $ 2解放し続けます。
5。結論
潮汐力散逸のため、ガリレオ衛星の軌道は時間とともにゆっくりと移行します。エネルギーは主に
イオと木星の間の潮汐力相互作用、しかしの影響その後、散逸は、衛星間で再分配されます
ラプラス共鳴。 10億年のタイムスケールで、これはイオ、エウロパ、ガニメデの外への移行。だから
現在、平均運動の共鳴に関与していない、カリストは非常に多く、これらのサイクルは何十億年も続くことがあります。各
新しい共鳴へのキャプチャは、新しい共鳴中心に向かって引き付けられる半長軸の小さなジャンプを生成します
線形ドリフトを再開する前に。
私たちの研究は、カリストとの共鳴的な出会いが明らかになりました
私たちが知っているように、ラプラス共鳴の特徴を破壊することができます
今日、イオとエウロパ間の2:1の共振(これは すべてのシミュレーションで持続します)。したがって、ラプラス共鳴
潮汐力散逸作用下では安定しているが、約1.5 Gyrsで発生するカリストとの共鳴的な出会い
今から。 4つの衛星すべてが常に最終的には
新しい共鳴チェーン、エウロパとガニメデがシミュレーションの37%で破壊されました。ラプラス
共鳴は、イオ、エウロパ、ガニメデの間の純粋な3体共鳴に変わります。ただし、これはまれな結果です
通常は数億年未満のシミュレーションの結果であり、です。この時間間隔の間に、エウロパの離心率が増加します。
衛星の軌道の傾きが再生されない
長期的なダイナミクスにおける役割:それらはまったく小さいままです
時と衛星のわずかな変化によってのみ影響を受けます
共鳴に入る、または共鳴から出る。このアプローチには、主に2つの制限があります。最初はハミルトニアンは、離心率の2次で切り捨てられます。
次のように、偏心が大きい場合、モデルの精度は低下します。
ケースBのいくつかのシミュレーション。これは最終結果に影響を与える可能性があります。
いくつかのシミュレーションのうち、分類スキームもこの結論で示されたパーセンテージ。さらに重要なのは、
高速角度でハミルトニアンを平均化するプロセス、多くの純粋な三体の組み合わせが削除され、特に
離心率の次数0の項。私たちが観察したのでシステムは、多数の弱い共振に閉じ込められる可能性があります。
平均化されていないモデルによって与えられる長期的な進化は、おそらくさらに共鳴的な捕獲を示し、
カリストはさらにありそうもない。ただし、追加の3体共鳴も、
ケースBを作成し、さらにシミュレーションをケースAに進めます。割合
したがって、私たちの研究で得られたものは指標とみなされるべきです。残念ながら、非平均を使用した5 Gyrsを超える統計研究
モデルでは、法外な計算時間が必要になります。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます